Սկիզբը
Նախորդ հատվածը
Գլուխ 8
Շատ մեծ և շատ փոքր
10 թվի էլի մեկ առավելություն
Պատճառներից մեկը, որը համառորեն ստիպեց գիտնականներին գործնական կիրառության մեջ ներմուծել աստիճանային (էքսպոնենտալ) թվերը, շատ մեծ կամ շատ փոքր թվերով աշխատելու անհրաժեշտությունն էր: Օրինակ, Երկրի զանգվածը մոտավորապես հավասար է 6000000000000000000000000000 գրամի, իսկ ջրածնի ատոմի զանգվածը՝ 0,00000000000000000000000166 գրամի:
Իհարկե, նկատեցիք, որ այսպիսի գրառման ժամանակ դժվար չէ մեկ կամ մի քանի զրո կորցնելը: Աշխատանքի ընթացքում գիտնականները թվերն արտահայտելու նոր մեթոդ մշակեցին, երբ թվի մի մասը սովորական թիվ է, իսկ մյուս մասը՝ աստիճանային: Աստիճանային թվի հիմքը 10 թիվն է (նախորդ գլխի վերջում ես այդ հնարավորության մասին ակնարկեցի):
10 թվի աստիճանները թույլ են տալիս հարմար տեսքով ներկայացնելու ինչպես շատ մեծ, այնպես էլ շատ փոքր թվերը: Դա երևում է ներքևում բերված աղյուսակից, որը կարող եք ինքնուրույն հաշվարկներ կատարելով ստուգել:
1000000=106
100000=105
10000=104
1000=103
100=102
10=101
1=10°
0,1=10-1
0,01=10—2
0,001=10—3
0,0001=10—4
0,00001=10—5
0,000001=10—6
Որպեսզի համոզվենք, որ 10 թիվը լավ է ներառվում մեր հաշվարկման համակարգում, դիտարկենք 4372,654 թիվը: Այն կարգերի վերլուծենք և կստանանք 4 հազար, 3 հարյուր, 7 տասնյակ, 2 միավոր, 6 տասնորդական, 5 հարյուրերորդական և 4 հազարերորդական: Այժմ հիշենք, որ 1000=103, 100=102, 10=101 և այլն, և գրառենք 4372,654 թիվն այսպես՝ (4х103)+(3х102)+(7х101)+(2х10°)+(6х10—1)+(5х10—2)+(4х10—3): Այսպիսով, թղթի վրա գրեցինք այն գործողությունները, որոնք արդեն հազար տարի համրիչների վրա կատարում են: Եթե հաշվիչների վրա միավորների շարքը նշենք «զրո», միավորի շարքից բարձր տեղակայված շարքերը կնշանակենք 1, 2, 3 և այլն, իսկ միավորի շարքից ցածր շարքերը, համապատասխանաբար -1, -2, -3, ապա յուրաքանչյուր շարք 10 թվի աստիճանացույցին է համապատասխանում: Թվաբանության բոլոր դրույթները, որոնք սովորել ենք՝ օգտագործելով արաբական թվերը, կարելի է հեշտությամբ բացատրել այս աստիճանացույցերի օգնությամբ, ինչը դպրոցներում, սովորաբար չեն անում:
Մի քիչ ժամանակ կկորցնենք, որպեսզի աստիճանային թվերից գլուխ հանենք, հետագայում այն նշանակալի կթեթևացնի թվերի հետ աշխատանքը:
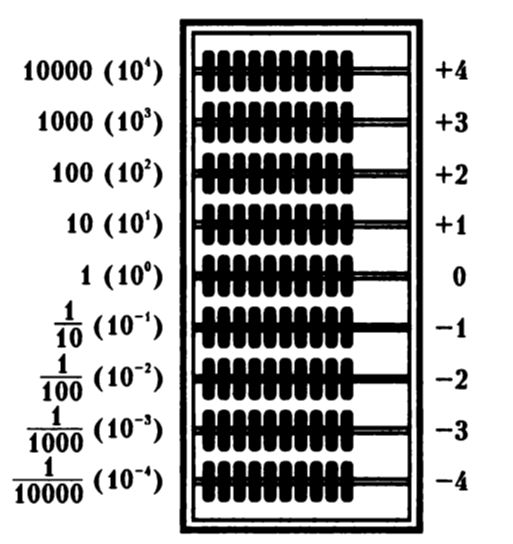
Սկզբում դիտարկենք 10 թվի դրական աստիճանները: Նկատենք, որ տվյալ դեպքում աստիճանացույցը հավասար է սովորական թվի զրոների քանակին: Այսպիսով, եթե զրոների քանակը 1000000-ում հավասար է վեցի, ապա այս թվի աստիճանային տեսքը կլինի 106 (նկարում՝ համրիչ, որի շարքերը նշանակված են 10-ի աստիճաններին համապատասխան):
Այժմ, երբ անհրաժեշտ է ոչ միայն մեկերից և զրոներից կազմված թիվը ներկայացնել աստճանային տեսքով, պետք է այն 10-ի ինչ-որ աստիճան պարունակող արտահայտության տեսքով գրել: Օրինակ, երկրի զանգվածը, ինչպես պարզեցինք գլխի սկզբում, հավասար է 6000000000000000000000000000 գրամ: Այս թիվը կարելի է ներկայացնել ինչպես 6х1000000000000000000000000000 գրամ: Այժմ այս արտահայտության ամենամեծ թիվը կազմված է մեկից և շատ քանակի զրոներից, այսինքն՝ այն կարելի է աստիճանի տեսքով ներկայացնել: Քանի որ զրոների քանակը 27 է, թիվը կարելի է գրել 1027տեսքով: Այժմ Երկրի զանգվածը կարելի է աստիճանային տեսքով ներկայացնել` 6х1027 գրամ: Մեծ թվերը աստիճանային արտահայտության տեսքով ներկայացնելը երկու ակնհայտ առավելություն է տալիս:
Նախ՝ այսպիսի գրելաձևը շատ սեղմ է, և երկրորդ՝ ավելի հեշտ է կարդալ, զրոների ահռելի քանակը հաշվելու անհրաժեշտություն չկա:
Փոքր թվերը նշանակելու համար օգտագործում են 10-ի բացասական աստիճանները: Ինչպես երևում է աղյուսակից, 10 թվի բացասական աստիճանը, սովորական թիվ է ներկայացնում, տասնորդական ստորակետից աջ տեղակայված համապատասխան զրոներից բաղկացած և մեկով վերջացող տասնորդական կոտորակ: Բացասական աստիճանացույցի թվային արժեքը հավասար է ստորակետից հետո եղած զրոների քանակին գումարած 1:
Օրինակ՝ 0,000001թիվը ստորակետից հետո հինգ զրո ունի, հետևաբար, աստիճանային տեսքով այն կգրենք այսպես` 10—6:
Ջրածնի ատոմի զանգվածը կարելի է ներկայացնել 1,66х0,000000000000000000000001 գրամ արտահայտության տեսքով: (Եթե բազմապատկում կատարեք, ապա կստանաք այն արժեքը, որը բերված է գլխի սկզբում:) Երկրորդ արտադրիչը 10-ն է բացասական աստիճանացույցով, այն տասնորդական նշանից աջ 23 զրո ունի: Այսպիսով, աստիճանային տեսքով այն կգրվի՝ 10—24: Ջրածնի ատոմի զանգվածը 1,66 անգամ մեծ է այս արժեքից, հետևաբար, ջրածնի ատոմի զանգվածը հավասար է 1,66 х 10—24.
Տասից տարբեր թվեր
Հիմա, երբ սովորեցինք 10 հիմքով աստիճանային թվերն օգտագործելը, հեշտ կլինի այլ հիմքերով աստիճանային տեսքից գլուխ հանելը: Մեր գրքի սկզբում արդեն ասել եմ, որ որոշակի դեպքերում 10-ի փոխարեն հարմար է օգտագործել 12 թիվը, քանի որ 12 թիվն ավելի շատ բաժանարարներ ունի, քան 10-ը: (12 թիվը բացի բաժանարարների քանակից, ուրիշ առավելություններ էլ ունի:)
Մարդիկ հնում ժամանակը լուսնի միջոցով էին որոշում: Յուրաքանչյուր 29 կամ 30 օրը մեկ նոր լուսին էր դուրս գալիս, և հետևաբար, սկսվում էր նոր ամիսը: Տարվա մեջ այդպիսի ամիսները, այսինքն` մի գարունից մյուսը, 12 էին, ավելի ստույգ 12 ամիս և 11 օր: Սա 12 թվին յուրահատուկ մոգական նշանակություն տվեց, իսկ հնագույն մարդու համար դա շատ կարևոր էր: Կենդանակերպի 12 նշան կա, որոնցից յուրաքանչյուրում Արևը Երկրի շուրջ իր թվացյալ պտույտի ժամանակ, մեկ ամիս լինում է: Կենդանակերպի նշանների քանակն իր արտացոլումն ստացավ նաև երկրային գործերում: Դա Իսրայելի 12 ցեղերը և 12 սուրբ առաքյալներն են:
Եթե ուզում ենք 12-ը որպես հաշվարկման համակարգի հիմք օգտագործել, անհրաժեշտ է տասներկու տարբեր թվանշան՝ ներառյալ զրոն։ Մեզ մոտ այդ թվանշանները կլինեն 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, @ և #: @ և # նշաններն օգտագործում եմ այն թվերի նշանակման համար, որոնք տասական համակարգում նշանակվում են 10 և 11:
222 թիվը տասական համակարգում, այսինքն՝ 10 հիմքի վրա հիմնված համակարգում, կարելի է գրել այսպես`(2х102)+(2х10′)+(2х10°): Տասներկուական համակարգի այդպիսի թիվը կարելի է փոխակերպել տասական համակարգի՝ այն գրելով հետևյալ տեսքով. (2х122)+(2х121)+(2х12°): Հաշվարկները կատարենք և կստանանք՝ 288+24+2, կամ 314: Այլ կերպ ասած, 12 հիմքով համակարգի, այսինքն՝ տասներկուական համակարգում 222 թիվը, հավասար է 10 հիմքով համակարգի, այսինքն՝ տասական համակարգի 314 թվին:
Տասներկուական համակարգում թիվը կարելի է գրել, ասենք, ինչպես 3#4: Այն համարժեք է (3х122)+(#х12′)+(4х12°): Նախօրոք պայմանավորվել էինք, որ տասներկուական համակարգում #-ը հավասար է 11, հետևաբար տասական համակարգում կստանանք 432+132+4, կամ 568:
Հաշվարկման համակարգի համար որպես հիմք կարելի է և 10-ից փոքր թիվ վերցնել: Վերցնենք 7 թիվը, համակարգը կանվանենք յոթական: Այդ դեպքում մեզ միայն 7 նշան է անհրաժեշտ՝ 0, 1, 2, 3, 4, 5 և 6: Յոթական համակարգի 435 թիվը տասական համակարգում կարելի է գրել այսպես` (4х72)+(3х71)+(5х7°), որը հավասար է 196+21+5, կամ 222:
Այս եղանակը թույլ է տալիս թիվը մեկ հաշվարկման համակարգից փոխակերպել ցանկացած այլ համակարգի, ընդ որում այն կիրառելի է նույնիսկ տասնորդական կոտորակների համար:
0,15 արտահայտությունը տասներկուական համակարգում կարող է ներկայացվել (1х12—1)+(5х12—2), կամ 1/12+5/144, որը տասական համակարգում հավասար է 17/144:
Յոթական համակարգում նույն արտահայտությունը կարելի է ներկայացնել այսպես`(1х7—1)+(5х7—2), կամ 1/7+5/49, որը տասական համակարգում հավասար է 12/49։
Այժմ եկեք պարզենք, թե ինչպես որոշել յուրաքանչյուր հաշվարկման համակարգի համար անհրաժեշտ առանձին նշանների քանակը: Առաջին թիվը, որի համար երկու նշան է հարկավոր 10-ն է (ցանկացած համակարգում): 10-ից փոքր բոլոր թվերի համար անհրաժեշտ են առանձին և տարբեր նշաններ: 10-ից մեծ բոլոր թվերը կարելի է գրառել 10-ից փոքր թվանշանների համադրությունների միջոցով: Ակնհայտ է, որ այս կանոնը ճշմարիտ է տասական համակարգի համար, որի հետ շատ լավ ծանոթ ենք: Կարելի է ենթադրել, որ ուրիշ համակարգերում այս կանոնը նույնպես ճշմարիտ է (որում կարող ենք գործնականում համոզվել):
Եկեք պարզենք, թե ինչի է հավասար 10 արտահայտության արժեքը, օրինակ, տասներկուական համակարգում: Այն հավասար է (1х12-1)+(0х12°), կամ 12+0, կամ 12՝ տասական համակարգում: Նմանապես, յոթական համակարգում 10 արտահայտության արժեքը հավասար է (1х7-1)+(0х7°), կամ 7+0, կամ 7: Կարելի է համանման գործողություններ կատարել ուրիշ համակարգերի համար և, շուտով կհամոզվենք, որ որևէ թվի վրա հիմնված համակարգում 10 արտահայտությունը համապատասխանում է հենց այդ թվին: (Տասական համակարգում 10-ը, բնականաբար, հավասար է 10)։
Տասներկուական համակարգում 12-ից փոքր յուրաքանչյուր թվի համար անհրաժեշտ է առանձին թվանշան, այսինքն 12 տարբեր թվանշան՝ ներառյալ զրոն: Յոթական համակարգում 7-ից փոքր յուրաքանչյուր թվի համար անհրաժեշտ է առանձին թվանշան, այսինքն 7 տարբեր թվանշան՝ ներառյալ զրոն: Այս կանոնը բոլոր հաշվարկման համակարգերի համար ճիշտ է: Ասենք, 28 հիմքով հաշվարկման համակարգի համար, մեզ անհրաժեշտ է 28 տարբեր թվանշան՝ ներառյալ զրոն:
Որպեսզի օգնեմ այս կանոններից ավելի լավ գլուխ հանելուն, առաջին երեսուն թվերի համար նշանների աղյուսակ եմ բերում տասներկուական համակարգում, յոթական համակարգում և մեզ լավ ծանոթ տասական համակարգում:
| Յոթական համակարգ | Տասական համակարգ | Տասներկուական համակարգ |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | 3 |
| 4 | 4 | 4 |
| 5 | 5 | 5 |
| 6 | 6 | 6 |
| 10 | 7 | 7 |
| 11 | 8 | 8 |
| 12 | 9 | 9 |
| 13 | 10 | @ |
| 14 | 11 | # |
| 15 | 12 | 10 |
| 16 | 13 | 11 |
| 20 | 14 | 12 |
| 21 | 15 | 13 |
| 22 | 16 | 14 |
| 23 | 17 | 15 |
| 24 | 18 | 16 |
| 25 | 19 | 17 |
| 26 | 20 | 18 |
| 30 | 21 | 19 |
| 31 | 22 | 1@ |
| 32 | 23 | 1# |
| 33 | 24 | 20 |
| 34 | 25 | 21 |
| 35 | 26 | 22 |
| 36 | 27 | 23 |
| 40 | 28 | 24 |
| 41 | 29 | 25 |
| 42 | 30 | 26 |
Զրոների և մեկերի օգնությամբ ենք հաշվում
Յուրաքանչյուր հաշվարկման համակարգի համար կարելի է գումարման և մյուս թվաբանական գործողությունների աղյուսակներ կազմել: Տասներկուական համակարգում 5+8=11, իսկЗх4=10: Յոթական համակարգում 3+6=12, իսկ 5х3=21: Մեզ սա կարող է տարօրինակ թվալ, քանի որ այդպիսի համակարգեր չենք օգտագործում: Սակայն, եթե բոլոր հաշվարկներն այդպիսի համակարգերից մեկի շրջանակում կատարենք, կտեսնենք, որ համակարգը նույնպես համապատասխանում է ներկայացված նպատակներին: Մարդկությունը կանգ է առել տասական համակարգի վրա, հենց այն պարզ պատճառով, որ մարդու ձեռքերին տասը մատ կա, այլ ոչ թե որ այս համակարգն ավելի տրամաբանական է, քան ցանկացած ուրիշը: Սակայն առանձին դեպքերում և կոնկրետ նպատակների համար կարող է թվալ, որ ինչ-որ հաշվարկման համակարգ ավելի գործուն է, քան ուրիշները: Սա ճշմարիտ է 2 հիմքով համակարգի դեպքում, այսինքն՝ երկուական համակարգի համար: Երկուական համակարգում 10 արտահայտությունը տասական համակարգում 2 է:
Հետևաբար, այդպիսի համակարգում միայն երկու թվանշան կա` 0 և 1: Նախորդ էջերում այդպիսի համակարգի առաջին թվերի համար սիմվոլներ և տասական համակարգի համապատասխան համարժեքներ են բերված:
Թվերի փոխակերպումը երկուական համակարգից տասական համակարգին դժվար չէ: Օրինակ, երկուական համակարգում դիտարկենք 11001 արտահայտությունը: Այն համարժեք է (1х24)+(1х23)+(0х22)+(0х21)+(1х20), կամ 16+8+0+0+1, կամ 25, որն էլ համապատասխանում է աղյուսակում բերված համարժեքին:
Այս գործընթացը կարելի է հեշտացնել, եթե հաշվի առնենք, որ 2 թվի աստիճանը բազմապատկվում է կա՛մ 0-ով, և արդյունքը նույնպես հավասար կլինի զրոյի, և այն կարելի է անտեսել, կա՛մ 1-ով, և այդ ժամանակ ուղղակի 2 է, ինչ-որ աստիճան է:
Այսպես, կարող ենք կարգային համարը գրել աջից ձախ, ինչպես ներքևում մանր թվերով ցույց է տրված.

Յուրաքանչյուր մանր թիվը 2 թվի աստիճանն է, երկուական համակարգում ներկայացված թվանշանի դիրքը որոշող թվով: Պետք է հաշվի առնել միայն այն ցուցիչները, որոնք դրված են մեկերի դիմաց: Զրոների դիմաց գրված ցուցիչները կարելի է բաց թողնել: Այդպիսի մոտեցմամբ կարելի է 11001թիվը գրել այսպես` 24+23+20, կամ 16+8+1, կամ 25:
Մեծ թվերը, ինչպես՝ 1 110 010 100 001 001, կարելի է տասական համակարգ փոխակերպել նույն եղանակով:

Քանի որ մեկերին համապատասխանում են 0, 3, 8, 10, 13, 14 և 15 դիրքերը, ապա թիվը հավասար կլինի 215+214+213+210+28+23+20, կամ 32768+16384+8192+1024+256+8+1, կամ 58633:
Տասական համակարգից երկուական համակարգի հակադարձ փոխակերպումն այնքան էլ դժվար չէ, սակայն ավելի երկար է: Դիցուք, 1562 թիվը ներկայացված է տասական համակարգում: Երկուական համակարգ այն կարելի է փոխակերպել հետևյալ կերպ։
Երկուսի ամենաբարձր աստիճանը, որը 1562-ից փոքր է, 210-ն է (կամ 1024): Եթե 1562-ից հանենք1024, կմնա 538: Այժմ երկուսին համապատասխանող ամենամեծ աստիճանը, որը փոքր է 538-ից, 29-ն է (կամ 512): 538-ից այս թիվը հանելուց հետո կմնա 26: Մոտակա ամենաբարձր աստիճանը, որը դեռ փոքր է, 24-ն է (կամ16): Հանելուց հետո կմնա 10: Այժմ մոտակա թիվը 23-ն է (կամ 8): Հանելուց հետո կմնա 2 կամ 21: Այսպիսով, 1562=210+29+24+23+21։
Այժմ պետք է միայն աստիճանացույցները աջից ձախ ճիշտ տեղերում դասավորել: Մեկերը կդասավորենք 1, 3, 4, 9 և 10-րդ դիրքերում: Մնացած դիրքերում զրոներ կդնենք: Այսպիսով, կստանանք 11000011010 թիվը՝ տասական համակարգում 1562 թվի համարժեքը երկուական համակարգում:
Երկուական համակարգում գումարման և բազմապատկման աղյուսակները շատ պարզ են:
0+0=0 0+1=1 1+1=10
0x0=0 0x1=0 1×1=1
Ահա ամբողջ ցանկը:
Այսպիսով, երկուական համակարգում.
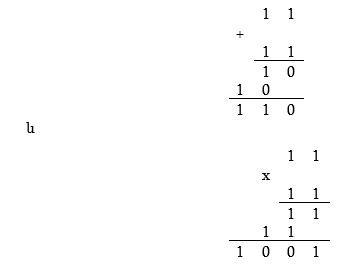
Այս հաշվումների ճշտությունը, ցանկության դեպքում կարելի է ստուգել, հաշվի առնելով, որ երկուական համակարգի 11, 110 և 1001-ը թվերը տասական համակարգում համապատասխանաբար հավասար են 3, 6 և 9-ին:
Այժմ պատկերացրեք, որ անջատիչների հավաքածուով էլեկտրոնային հաշվիչ մեքենա ունեք (օրինակ, կիսահաղորդչային): Յուրաքանչյուր անջատիչը կարող է լինել երկու դիրքերից մեկում՝ «միացած» (երբ հոսանք է անցնում է անջատիչի միջով) կամ «անջատած» (երբ հոսանք չի անցնում անջատիչի միջով):
Այժմ ենթադրենք, որ «միացած» դիրքը համապատասխանում է 1, իսկ «անջատած» դիրքը՝ 0-ի: Այս դեպքում հաշվիչ մեքենան կարելի է նախագծել այնպես, որ էլեկտրոնային ազդանշանի տարբեր անջատիչների անջատումները ենթարկվեն երկուական համակարգում մեկերով և զրոներով գումարման, բազմապատկման և ուրիշ գործողությունների կանոններին:
Այդպիսի մեքենան այնքան արագ կիրականացնի անջատումները և հաշվարկներ կանի այնպիսի արագությամբ, որ հաշված վայրկյանների ընթացքում կկատարի հաշվարկների այնպիսի ծավալ, որի համար մարդուց ամենաքիչը մեկ ամիս կպահանջվի:
Սակայն, հաշվարկման տարբեր համակարգեր ուսումնասիրելով, շատ ենք շեղվել մեր գրքի հիմնական թեմայից: Այժմ վերադառնում ենք տասական համակարգին, և հետագա ամբողջ տեղեկությունը կտրամադրվի հենց տասական համակարգում:
Աշխատում ենք աստիճաններով
Որպեսզի հստակ պարզենք, թե ինչպիսի գործողություններ կարելի է կատարել 10 հիմքով աստիճանային թվերով, սկսենք աշխատել համեմատաբար ոչ մեծ թվերի հետ, այլ ոչ թե երկրի զանգվածի նման հսկայական, որի մասին խոսվել է գլխի սկզբում:
Ենթադրենք, անհրաժեշտ է 3200 թիվը ներկայացնել աստիճանային տեսքով: Կարող ենք օգտագործել միայն ամբողջ թվեր, դրա համար էլ 3200 թիվը ներկայացնենք հետևյալ ձևով՝ (3х1000)+(2х100) կամ (3х103)+(2х102): Ավելի հարմար է այն դեպքերում, երբ հնարավոր է օգտվել մեկ աստիճանացույցից: Դրան կարելի է հասնել, տասնորդական թվեր օգտագործելով: 3200 թիվը ներկայացնենք 3,2х1000 տեսքով (կարող եք ինքնուրույն կատարել բազմապատկումը և ստուգել այս պնդման ճշտությունը) կամ 3,2х103:
Կարելի է, իհարկե, 3200-ը ներկայացնել այսպես` 32х100, որն էլ աստիճանային տեսքով կլինի 32х102: Կարելի է ընտրել հետևյալ տարբերակը՝ 3200=0,32х10000 կամ 0,32х104: Այս բոլոր արտահայտությունները նույնական են: Այս փաստը կարելի է հաստատել, բազմապատկման գործողություն կատարելով: Յուրաքանչյուր դեպքում 3200 կստանանք: Սակայն փաստը կարելի է հաստատել, առանց բազմապատկում կատարելու:
Ենթադրենք՝ պետք է 40-ը բազմապատկենք 50-ով: 40х50=2000։
Արտադրիչներից մեկը բաժանենք 2-ի, իսկ մյուսը բազմապատկենք 2-ով: Կստանանք 20х100, կամ 80х25: Երկու դեպքում էլ նույն արդյունքը կստանանք` 2000: Ենթադրենք, որ արտադրիչներից մեկը բազմապատկում ենք 10-ով, իսկ մյուսը բաժանում ենք 10-ի: Այդ ժամանակ կստանանք 4х500 կամ 400х5: Երկու դեպքում էլ արդյունքը նույնն է` 2000: Այլ կերպ ասած, երկու թվերի արտադրյալը չի փոխվի, եթե արտադրիչներից մեկը բազմապատկենք ինչ-որ թվով, իսկ մյուս բաժանենք նույն թվին:
Այժմ դիտարկենք 3,2х103: 3,2-ը բազմապատկենք 10-ով և 103-ը բաժանենք 10-ի: Ինչպես արդեն գիտենք, արդյունքը չի փոխվի: 3,2х10=32: 103-ը բաժանենք 10-ի (կամ միևնույն է, թե բազմապատկենք 10-1-ով) և կստանանք 102: Այժմ արտահայտությունն ունի հետևյալ տեսքը՝ 32х102. դրանից նրա արժեքը չի փոխվում:
Կարող ենք 3,2-ը բաժանել 10-ի (կստանանք 0,32) և 103-ը բազմապատկենք 10-ով (104): Արդյունքում կստանանք 0,32х104, այս դեպքում ևս արժեքը չի փոխվի:
Տեսնում ենք, որ 0,32х104, 32х102, 3,2х103 արտահայտությունները միևնույն թիվն են: Այդ դեպքում ի՞նչ իմաստ ունի մեկ տարբերակը մյուսով փոխարինելու: Հաշվարկների ճշգրտության տեսանկյունից ոչ մի իմաստ չունի, իսկ ահա հաշվարկներ կատարելու հարմարավետության տեսանկյունից, անշուշտ ունի: Նպատակահարմար է աստիճանային արտահայտության այնպիսի տարբերակն օգտագործելը, երբ ոչ աստիճանային թիվը 1-ից 10-ի միջև է: 32х102 դեպքում ոչ աստիճանային մասը մեծ է 10, իսկ 0,32х104 դեպքում`փոքր է 1-ից: 3,2х103 դեպքում ոչ աստիճանային մասը 1-ի և 10-ի միջև է, և սա հենց արտահայտության այն տեսքն է, որը սովորաբար օգտագործում են:
Մեկից փոքր թվերի համար, այս կանոնը նույնպես ճիշտ է, բացառությամբ աստիճանական մասին վերաբերող հատվածներին: Օրինակ, դիտարկենք 0,0054 թիվը: Այն կարելի է գրել ինչպես 54х0,0001 կամ ինչպես 5,4х0,001: Այս արտահայտություններից յուրաքանչյուրը բազմապատկումից հետո կտա միևնույն արդյունքը` 0,0054: Աստիճանական տեսքով այն կլինի ինչպես 54х10-4, 5,4х10-3 կամ 0,54х10-2:
Այս արտահայտությունները նույնպես համարժեք են: Ինչպես նախորդ օրինակում, կարող ենք բազմապատկել 5,4-ը 10-ով, իսկ 10-3 բաժանել 10-ի: 10-3 բաժանումը 10-ի համարժեք է 10-1 -ով բազմապատկելուն: Բաժանումը համարժեք է մեկ աստիճանացույցից մյուսը հանելուն (-3 — 1 = -4), այսինքն 10-3 բաժանել 10-ի հավասար է 10 -3-1 կամ10-4: Այսպիսով, 5,4х10-3 արտահայտությունը փոխակերպեցինք 54х10-4, չփոխելով նրա արժեքը:
Նմանատիպ գործողությունների օգնությամբ կարող ենք 5,4х10-3–ը փոխակերպել 0,54х10-2, չփոխելով նրա արժեքը: Սակայն գործնականում առավելությունը տրվում է 5,4х10-3 արտահայտությանը, քանի որ այս դեպքում ոչ աստիճանական մասը 1-ի և 10-ի միջև է:
Շարունակում ենք աստիճաններով աշխատելը
Աստիճանային թվերի համար կիրառական են նույն կանոնները, ինչ սովորական թվերի համար:
Գումարման և հանման գործողություններում մասնակցում են միայն ոչ աստիճանային մասը կազմող թվերը: Օրինակ, 2,3х104 և 4,2х104 թվերի գումարման արդյունքում կստանանք 6,5х104. Ստուգեք այս պնդումը՝ փոխակերպելով աստիճանային արտահայտությունը ոչ աստիճանայինի` 23000 և 42000: Գումարելով դրանք՝ կստանանք 65 000: Այսպիսի գործողություն կարելի է կատարել բոլոր այն օրինակների հետ, որոնք բերել եմ այս գլխում: Այսպիսով, ոչ միայն աստիճանային արտահայտությունների հետ շփվել կսովորեք, այլև գործնականում կհամոզվեք, որ պարտադիր չէ ամեն բանի հավատալ, ինչ ասում են, նույնիսկ եթե այդ «ինչ-որ բանը» տպագրված է։
8,7х104 և 3,9х104 թվերի գումարը 12,6х104 է: Պատասխանը կարելի է այս տեսքով թողնել, չնայած ոչ աստիճանային մասը 10-ից մեծ է: Կարելի է նաև վերը նշված բազմապատկման-բաժանման գործողությունների օգնությամբ արտահայտությունն ավելի հարմար տեսքի բերել` 1,26х105: Այս պատասխանը նույնքան ճիշտ է, որքան նախորդը:
Իսկ ինչպե՞ս վարվենք, երբ թվերի մոտ ցուցիչները տարբեր են: Ինչի՞ հավասար կլինի 1,87х104 և 9х102 թվերի գումարը: Որպեսզի գումարման գործողություն կատարենք, անհրաժեշտ է երկու թվերի աստիճանային մասերը նույն տեսքի բերել: Օրինակ, 1,87х104 կարելի է փոխակերպել 187х102: Արդեն կարելի է կատարել գումարումը՝ (9х102)+(187х102)=(9+187)х102=196х102: Կարելի է ուրիշ ճանապարհով գնալ և փոխակերպել 9х102-ը 0,09х104-ի, այդ ժամանակ կստանանք` (0,09х104)+(1,87х104)=(0,09+1,87)х104=1,96х104:
Այսպիսով, ստացանք երկու պատասխան՝ 196х102 և 1,96х104: Այս երկու արտահայտություններն էլ համարժեք են, բայց նախընտրելի է օգտագործել երկրորդը:
Աստիճանային թվերի հետ նմանապես կարելի է հանման գործողություն կատարել: Գործնականում, սակայն գումարման և հանման գործողություններ կատարելիս աստիճանային ձևից հազվադեպ են օգտվում, քանի որ հարմար է սովորական թվեր գումարել և հանելը: Սակայն բազմապատկման և բաժանման գործողությունների դեպքում աստիճանային թվերն անփոխարինելի են: Ենթադրենք, պետք է 60000-ը բազմապատկենք 0,008-ով: Սա դժվար չէ սյունակով կատարելը.
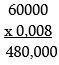
Տվյալ օրինակում միակ դժվարությունը զրոներով գործողությունն է: Պետք է ուշադիր հետևել տասնորդական ստորակետի դիրքին:
Այժմ փորձենք բազմապատկում կատարել, թվերի ներկայացման աստիճանային ձևն օգտագործելով: Թվերը փոխակերպենք ցուցչային տեսքի` 60000=6х104, 0,008=8х10-3. Բազմապատկենք այդ թվերը՝ 6х104х8х10-3: 6х8=48; ապա 104х10-3=101: (Գումարենք ցուցիչները` 4+(-3)=1)։ Պատասխանը կստանանք՝ 48х101, կամ, ավելի հարմար տեսքով, 4,8х102, կամ սովորական թվի տեսքով`480:
Ինչպես տեսնում ենք, աստիճանային տեսքն օգտագործելով, զգալի հեշտացնում ենք բազմապատկման գործողությունը, հատկապես այն դեպքերում, երբ գործ ունենք շատ մեծ և շատ փոքր թվերի հետ:
Ենթադրենք, պետք է այսպիսի խնդիր լուծել: Ջրածնի քանի՞ ատոմ կպարունակեր Երկիրը, եթե այն կազմված լիներ միայն ջրածնի ատոմներից:
Երկրի զանգվածը հավասար է 6000000000000000000000000000 գրամ, իսկ ջրածնի ատոմի զանգվածը` 0,00000000000000000000000166 գրամ: Որպեսզի գտնենք ջրածնի ատոմների քանակը, պետք է Երկրի զանգվածը բաժանենք ջրածնի ատոմի զանգվածի վրա, այսինքն՝ 6000000000000000000000000000-ը բաժանենք 0,00000000000000000000000166-ի: Իհարկե, եթե ուզում եք, կարող եք կատարել այս գործողությունը, բայց, թերևս, խելամիտ կլինի աստիճանային տեսքի անցնելը:
Աստիճանային արտահայտություններ օգտագործելու ժամանակ խնդիրն իսկույն հեշտանում է՝ (6х1027), (1,66х10-24): Ինչպես բազմապատման ժամանակ, կարելի է ոչ աստիճանային մի մասը բաժանել մյուսին: Այսպիսով, կստանանք մոտավոր 6:1,66=3,6 քանորդը (մոտավոր, սակայն այս խնդրի համար բավարար), միևնույն ժամանակ 1027:10-24=1051): Այսպիսով, Երկրի մեջ ջրածնի ատոմների քանակը (եթե այն կազմված լիներ միայն ջրածնի ատոմներից և ունենար այն զանգվածը, որն այժմ ունի) հավասար կլիներ 3,6х1051): Կամ սովորական թվի տեսքով 3600000000000000000000000000000000000000000000000000, եթե ուղղակի բազմապատկենք երկու սովորական թվեր, ինչպես անում էինք նախորդ բաժիններում:
Դժվարություն չի ներկայացնում նաև աստիճանային արտահայտությունների աստիճան բարձրացնելն ու նրանցից արմատ հանելը: Այսպես, (9х104)2 հավասար է 92х(104)2, որն էլ հավասար է 81х(104)2, կամ 81х108, կամ 8,1х109: Ճիշտ նույն կերպ էլ կարելի է (9х104)-ից արմատ հանել:
Քառակուսի արմատ 9х104(√9×10-4) հավասար է √9x√104 կամ 3х102:
Լրիվ անցնում ենք աստիճանների
Աստիճանային տեսքով թվերի օգտագործման մեջ դեռ անհասկանալի բաներ կան: Եթե շատ քանակով զրոներ պարունակով թվերի հետ գործ ունենք, ամեն ինչ բավականին պարզ է: Սակայն, ենթադրենք, որ պետք է բազմապատկենք 6837 և 1822 թվերը: Եթե այս թվերը գրենք աստիճանային տեսքով, կստանանք` 6,837х103 և 1,822х103: Աստիճանային մասերը բազմապատկելը դժվար չէ, իսկ ի՞նչ անենք 6,837 և 1,822 թվերը: Բախվեցինք միևնույն խնդրին, ինչպես մեծ թվերի բազմապատման ժամանակ, միայն այն տարբերությամբ, որ պետք է հետևենք տասնորդական ստորակետի դիրքին: Այլ կերպ ասած, պետք է թիվն այնպիսի տեսքով ներկայացնենք, որպեսզի ոչ աստիճանային մասը ինչքան հնարավոր է կարճ լինի կամ հավասարվի 1: Քանի որ խոսքը տասական համակարգի մասին է, մեզ պետք կլինեն տասի աստիճանները, որոնք քննարկեցինք յոթերորդ գլխի վերջում:
Այժմ եկեք մանրամասն ուսումնասիրենք 10 հիմքով աստիճաները: Սկսենք 10°=1 և 101=10-ից: Իսկ ինչի՞ են հավասար աստիճանները, երբ ցուցիչները 0-ի և 1-ի միջև են: Օրինակ, 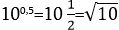 , որը մոտավորապես հավասար է 3,162278: Նման եղանակով (սակայն մեծ դժվարությամբ) կարելի է ստանալ 10-ի աստիճանների արժեքները 0-ից 1 ցուցիչների համար: Այս մեծությունները հաշվված և աղյուսակների տեսքով հավաքված են հատուկ տեղեկատուներում: Մեր գրքում բերված է 10 թվի տարբեր աստիճանների հակիրճ աղյուսակ:
, որը մոտավորապես հավասար է 3,162278: Նման եղանակով (սակայն մեծ դժվարությամբ) կարելի է ստանալ 10-ի աստիճանների արժեքները 0-ից 1 ցուցիչների համար: Այս մեծությունները հաշվված և աղյուսակների տեսքով հավաքված են հատուկ տեղեկատուներում: Մեր գրքում բերված է 10 թվի տարբեր աստիճանների հակիրճ աղյուսակ:
Քանի որ տվյալ դեպում հիմքում միշտ 10 թիվն է, աղյուսակում սովորաբար բերված են միայն աստիճանացույցները, այսինքն ցուցիչները: Առանձին գրված ցուցիչը անվանում են լոգարիթմ, աստիճանային արտահայտության արժեքը՝ սովորական թվի տեսքով, կոչվում է անտիլոգարիթմ: Օրինակ, 102=100 արտահայտության մեջ հետևյալ նշանակումները ճշմարիտ են.
2 — լոգարիթմ 100, իսկ 100 — անտիլոգարիթմ 2:
Ներքևում բերված է աղյուսակը, որում մի շարք լոգարիթմների համար անտիլոգարիթմներ են բերված, կոչվում է անտիլոգարիթմների աղյուսակ։
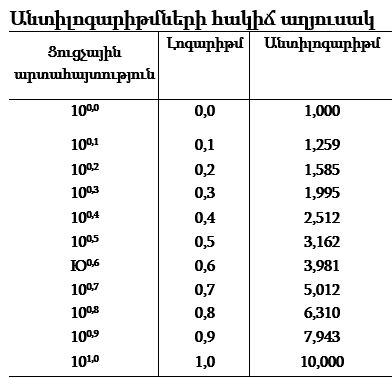
Աղյուսակում անտիլոգարիթմների մոտավոր արժեքներ են բերված, հնարավոր էլ չէ ճշգրիտ արժեքը բերել, որովհետև նրանք գոյություն ունեն միայն այնպիսի թվերի համար, ինչպես 100,0, 101,0 և այլն: Սակայն անտիլոգարիթմի մեծությունը կարելի է հաշվել այնպիսի ճշգրտությամբ (այսինքն՝ մինչև այնպիսի տասնորդական նշանի), որը պահանջվում է կոնկրետ տվյալ դեպքում:
Եթե գնանք հակառակ ուղղությամբ, կարող ենք 1-ից 10-ը ցանկացած թիվ ներկայացնել ինչպես10-ի որևէ աստիճան: Այլ կերպ ասած՝ համապատասխան մեթոդների օգնությամբ (դրանք մեր գրքում չենք քննարկի) յուրաքանչյուր թվի համար կարելի է համապատասխան լոգարիթմը հաշվել:
Ներքևում մի շարք սովորական թվերի համար լոգարիթմների հակիրճ աղյուսակ է բերված: Շարք տեղեկագրքերում կան լոգարիթմների մանրամասն աղյուսակներ, որոնցում կարելի է ցանկացած թվի համար լոգարիթմ գտնել:
Լոգարիթմների աղյուսակներ արդեն կազմված են, և ինքնուրույն հաշվարկներով զբաղվելու կարիքը արդեն չկա: Այդ աշխատատար գործն արդեն արված է: Միակ բանը, որը պետք է անել, լոգարիթմների աղյուսակում անհրաժեշտ արժեքը գտնելն է: Պատահականորեն ինչ-որ թիվ վերցնենք, օրինակ՝ 3,2, և ներքևում բերված աղյուսակում գտնենք լոգորիթմի արժեքը: 3,2-ի լոգարիթմը հավասար է 0,5051: Եվս մեկ օրինակ աղյուսակից՝ 2,4-ի լոգարիթմը հավասար է 0,3802: (Բնականաբար, սա լոգարիթմների մոտավոր արժեքն է)[1]:
Այժմ, երբ ունենք լոգարիթմների արժեքները, այսինքն՝ ցուցիչը, բազմապատկման և բաժանման գործողությունների ժամանակ կարող ենք դրանք օգտագործել:
Գիտենք, որ բազմապատկման ժամանակ աստիճանացույցները գումարվում են, նշանակում է 3,2 և 2,4 թվերը բազմապատկելու համար բավարար է գումարել նրանց լոգարիթմները՝ 0,5051 և 0,3802, որոնց գումարը հավասար է 0,8853: Սա միայն ցուցիչն է, այսինքն՝ թիվը, որը փնտրում ենք 100,8853-ն է: Այժմ պետք է նորից անտիլոգարիթմների աղյուսակին դիմենք և գտնենք 0,8853 անտիլոգարիթմը: Դա 7,68-ն է: Այսպիսով, 3,2х2,4=7,68:
Եթե ցանկանում ենք բաժանել 3,2–ը 2,4-ի, բավարար է 0,5051-ից հանենք 0,3802, որը հավասար է 0,1249: Այս թվի անտիլոգարիթմը 1,333 է, որն էլ պատասխանն է: Իսկ այժմ վերադառնանք օրինակին, որից սկսեցինք այս բաժինը` 6837х1822: Այս թվերը փոխակերպենք աստիճանային տեսքի և կստանանք (6,837 х 103) х (1822 х 103): 103-ի լոգարիթմը 3-ն է, քանի որ թվի լոգարիթմը այն աստիճանն է, որը պետք է բարձրացնենք 10-ը, որպեսզի տվյալ թիվը ստանանք: Իսկ որպեսզի 103 ստանանք, ակնհայտ է, պետք է 10 խորանարդ բարձրացնենք: Հենց այդպես էլ 1012 լոգարիթմը հավասար է 12, իսկ 10-14 լոգարիթմը հավասար է -14-ի:
6,837 թվի լոգարիթմը պետք է փնտրել լոգարիթմների ավելի մանրամասն աղյուսակում, քան այն, որը գրքում է բերված: Այն հավասար է 0,83487: Այդ ժամանակ 6,837 х 103 լոգարիթմը հավասար է 0,83487 + 3 (հիշեք, թվերի բազմապատկման ժամանակ գումարում ենք նրանց լոգարիթմները), կամ՝ 3,83487:
Նույն կերպ էլ աղյուսակից գտնում ենք 1,822-ի լոգարիթմը, որը հավասար է 0,26055, այսպիսով, 1,822 х 103 լոգարիթմը հավասար է 0,26055 + 3, կամ 3,26055:
Որպեսզի 6837 և 1822 թվերը բազմապատկենք, պետք է գումարել նրանց լոգարիթմները, իսկ հետո գտնել գումարի անտիլոգարիթմը: Այսպիսով, այդ թվերի արտադրյալի լոգարիթմը հավասար է 3,83487 + 3,26055, կամ 7,09542: Այս թիվը կարելի է ներկայացնել ինչպես 0,09542+7: Թվի տասնոդական մասը, տվյալ դեպքում՝ 0,09542, անվանում են մանտիս, իսկ ամբողջը, տվյալ դեպքում՝ 7, բնութագիր:
Թվի անտիլոգարիթմն ուղղակի 10 թիվն է, բարձրացրած այդ աստիճանը: 0,09542-ի անտիլոգարիթմը (աղյուսակով որոշված) հավասար է 1,246, իսկ 7-ի անտիլոգարիթմը` 107: Լոգարիթմից անտիլոգարիթմին անցնելու ժամանակ գումարումը բազմապատկումով է փոխարինվում: Այսպիսով, անտիլոգարիթմը հավասար է 1,246х107: Կամ սովորական, ոչ ցուցչային տեսքով` 12460000:
Եթե պարզապես սյունակով բազմապատկենք 6837-ը 1822-ով, 12457014 կստանանք: Սակայն չպետք է մոռանալ, որ լոգարիթմների մոտավոր արժեքներն են, այնպես որ և արդյունքը կարող ենք միայն որոշակի մոտավորությամբ ստանալ:
Որպեսզի 6837-ը բաժանենք 1822-ի, պետք է առաջին թվի լոգարիթմից հանենք երկրորդ թվի լոգարիթմը, կամ 3,83487-3,26055=0,57432: Այս թվի անտիլոգարիթմը հավասար է 3,752: Սա էլ հենց փնտրվող պատասխանն է: Եթե սյունակով բաժանում կատարեք, ապա կստանաք ավելի ճշգրիտ պատասխան` 3,75192: Բայց ինչպես արդեն գիտենք, լոգարիթմները մոտավոր արժեքներ են:
Հնարավոր է, հաշվարկի այսպիսի մեթոդը դժվար և անարդյունավետ թվա, ախր բավական չէ, որ մոտավոր արժեք ենք ստանում, դեռ պետք է պատասխաններն էլ երկու աղյուսակներում փնտրենք: Ավելի հե՞շտ չէ սյունակով բազմապատկում կատարելը: Սակայն ինժեներական և գիտական հաշվարկների համար հաճախ բավարար է այն ճշգրտությունը, որը լոգարիթմական մեթոդն է տալիս: Միևնույն ժամանակ հաճախ ստիպված ենք բազմապատկաման և բաժանման բազմաթիվ գործողություններ կատարել, և լոգարիթմական մեթոդը պարզապես անփոխարինելի է: Ենթադրենք, պետք է այսպիսի օրինակ լուծել՝ (194,768х0,045х19,22):(1,558х35,4):
Բավականին շատ ժամանակ պետք կլինի, որպեսզի բազմապատկման և բաժանման բոլոր անհրաժեշտ գործողությունները կատարեք, իսկ լոգարիթմների մեթոդն օգտագործելով, եթե լավ եք յուրացրել լոգարիթմական աղյուսակներով աշխատելու կանոնները, կարելի է այդ օրինակը շատ արագ լուծել: Պետք կլինի մի քանի անգամ նայել աղյուսակներին և կատարել մի քանի գումարման և հանման գործողություն:
Հետագայում, եթե խնդրի պայմաններով բավարար է որոշակի մոտավորությամբ պատասխան ստանալ, իսկ ինժեներական և գիտական հաշվարկներով հենց այդ էլ պահանջվում է, լոգարիթմների մեթոդը լրացուցիչ առավելություն է տալիս, քանի որ այն էականորեն կրճատում է անհրաժեշտ հաշվարկներ կատարելու ժամանակը:
Նոր համրիչներ
Լուծելու ժամանակի կրճատման բանալին կգտնենք, եթե լոգարիթմական կախվածության բնույթին ուշադրություն դարձնենք: 1,0-ի լոգարիթմը հավասար է 0,0000, 2,0-ի լոգարիթմը` 0,3010-ը, իսկ 3,0-ինը` 0,4771-ի: 1-ից 2-ը թվի մեծանալու հետ լոգարիթմի արժեքը մեծանում է 0,3010-ով; 2-ից 3-ը թվի մեծանալու հետ լոգարիթմի արժեքը մեծանում է 0,1761-ով: 4,0-ի լոգարիթմը հավասար է 0,6020, որն էլ նշանակում է 0,1249-ով ավելացում: 9,0-ից 10-ը թվի մեծանալու հետ լոգարիթմի արժեքը մեծանում է 0,9542-ից 1,0000-ը, այսինքն՝ միայն 0,0458: 19-ից 20-ի անցման ժամանակ լոգարիթմը մեծանում է 1,2788-ից 1,3010-ը, այսինքն միայն 0,0222:
Այժմ քանոնի մի կողմում գրենք լոգարիթմի արժեքները՝ տեղադրելով հավասարաչափ, իսկ մյուս կողմում` այդ լոգարիթմներին համապատասխան թվերը (անտիլոգարիթմները):
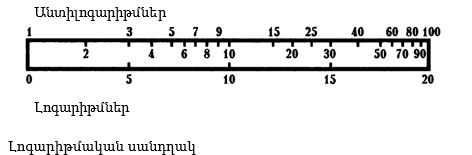
Տեսնում ենք, որ թվերի մեծանալուն զուգընթաց սովորական թվերն ավելի խիտ են դասավորվում: Դա արտացոլում է այն փաստը, որ թվերի մեծանալուն զուգընթաց լոգարիթմի մեծանալու արագությունը նվազում է:
Սանդղակը, որի վրա թվերը հավասարաչափ չեն դասավորված, այլ իրենց լոգարիթմական մեծության համապատասխան, կոչվում է լոգարիթմական սանդղակ: Այս լոգարիթմական սանդղակն էլ հաշվարկներ կատարելու համար շատ կարևոր մի գործիքի՝ լոգարիթմական քանոնի հայտնաբերման հիմքը դարձավ, որը անհրաժեշտ էր յուրաքանչյուր ինժեներին, նախքան հաշվիչները և համակարգիչները դրան փոխարինելու եկան:
Քանոնը հետևյալ կերպ է կառուցված: Եթե երկու սովորական քանոն, որոնց վրա լոգարիթմական սանդղակներ կան, շարժենք մեկմեկու հանդիման, կարելի է գումարման և հանման գործողություն կատարել, իսկ քանի որ քանոնի սանդղակները լոգարիթմական են, նշանակում է, որ գումարում կամ հանում ենք լոգարիթմական թվեր, այսինքն՝ բազմապատկում կամ բաժանում ենք հենց թվերը:
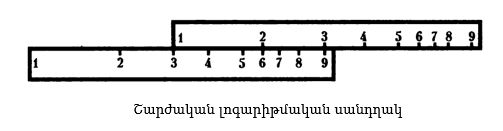
Օրինակ՝ պետք է 2-ն ու 3-ը բազմապատկենք: Ինչպես նկարում է ցույց տված, քանոնի շարժական մասն այնպես դնենք, որպեսզի նրա 1-ի բաժանումը համընկնի անշարժ հատվածի 3-ի բաժանման հետ: Այնուհետև ուշադրություն ենք դարձնում շարժական մասի 2-ի բաժանմանը և նայում ենք, թե անշարժ մասի որ բաժանման դիմաց է այն կանգնել: Տեսնում ենք, որ 6-ն է: Այսինքն՝ լոգարիթմ3+լոգարիթմ2=լոգարիթմ6, իսկ 3×2=6:
Հաջորդ նկարում ցույց է տրված մի քանի սանդղակներով իրական լոգարիթմական քանոնի ուրվագիծը: Այսպիսի քանոնը տարբեր խնդիրներ արագ լուծելու հնարավորություն է տալիս և կատարելու բարդ հաշվարկներ, որոնց ճշգրտությունը կախված է սանդղակների բաժանումների չափսերից:
Փաստացի՝ այսպիսի քանոնը կոմպակտ լոգարիթմական աղյուսակ է:

Սակայն յուրաքանչյուր նոր ձեռք բերում սովորաբար ինչ-որ կորուստով է ուղեկցվում: Հենց այդպիսին է վիճակը նաև լոգարիթմական քանոնի դեպքում: Քանոնը թույլ է տալիս շատ ավելի արագ և հարմար հաշվարկներ կատարել, սակայն կորուստներ էլ կան: Լոգարիթմական աղյուսակի օգտագործման ժամանակ հարկավոր չէ տասնորդական ստորակետի դիրքը որոշել, այն արդեն աղյուսակում նշված է: Քանոնով հաշվարկների ժամանակ տասնորդական ստորակետի դիրքն ինքներս պետք է որոշեք: Որպեսզի տասնորդական ստորակետի դիրքը որոշեք, անհրաժեշտ է լուծվող խնդրի պատասխանը կոպիտ գնահատել: Օրինակ`հաշվում ենք արտահայտությունը, որն այս գլխի սկզբում դիտարկում էինք՝ (194,768х0,045х19,22):(1,558х35,4)։
Կլորացնենք այս արտահայտության թվերը և կստանանք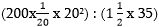 , որը հավասար է (4000:50), կամ 80: Նշանակում է, որ վերը նշված արտահայտությունը ճիշտ լուծելով, մեր ստացած պատասխանը կգտնվի 80 թվին ավելի մոտ, քան 8-ին կամ 800-ին: Այսպիսով, գնահատեցինք տասնորդական ստորակետի դիրքը, կամ այլ կերպ ասած, ապագա պատասխանի «արժեքի կարգը»:
, որը հավասար է (4000:50), կամ 80: Նշանակում է, որ վերը նշված արտահայտությունը ճիշտ լուծելով, մեր ստացած պատասխանը կգտնվի 80 թվին ավելի մոտ, քան 8-ին կամ 800-ին: Այսպիսով, գնահատեցինք տասնորդական ստորակետի դիրքը, կամ այլ կերպ ասած, ապագա պատասխանի «արժեքի կարգը»:
Այժմ, օգտագործելով լոգարիթմական քանոնը, կարելի է կատարել տրված գործողությունը: Արդյունքում կստանանք 587 պատասխանը, քանի որ գիտենք, որ պատասխանը պետք է ավելի մոտ լինի 80-ին, քան 8-ին կամ 800-ին, ապա տասնորդական ստորակետը վստահորեն կարելի է դնել աջից երկրորդ թվանշանից հետո, այսինքն՝ կստանանք 58,7: Լոգարիթմական քանոնի օգնությամբ կատարված բոլոր հաշվարկները, այդ թվում՝ արժեքի կարգի որոշումը, ընդամենը 35 վայրկյան խլեցին ինձանից, չնայած հաշվել եմ առանց շտապելու, որպեսզի սխալներ չանեմ:
Եթե լուծենք այս օրինակը՝ սյունակով (տակետակ) բազմապատկում և բաժանում կատարելով, կարող ենք ավելի ճշգրիտ պատասխան ստանալ: Ես կատարեցի այդ հաշվումները և ստացա 58,6: Սակայն հաշվումների ընթացքում երկու սխալ թույլ տվեցի, որոնք ստիպված էի ուղղել, և հաշվարկներ անելու համար ինձ անհրաժեշտ եղավ 20 րոպե: Չեմ կարող եմ ասել, որ գործընթացն ինձ հաճույք պատճառեց: Սկզբում տարբերություններ գտա քանոնով հաշվարկի արդյունքների հետ, հետո ստիպված էի հաշվարկի յուրաքանչյուր փուլը ստուգել և համեմատել քանոնով հաշվարկի արդյունքների հետ:
Ժամանակակից գրպանի հաշվիչները և համակարգիչները, իհարկե, բոլոր տեսակի հաշվարկներն ավելի են հեշտացրել: Սակայն երբեմն մտածում եմ, որ եթե ժամանակակից գիտնականը հնագույն գիտնականի նոր մարմնացումն է, ապա գրպանի հաշվիչը ուղղակի հնագույն համրիչի նորագույն վերարտադրությունն է:
Շարունակությունը
Թարգմանություն ռուսերենից
Թարգմանիչ՝ Մանուշակ Աբրահամյան
Խմբագիր՝ Գևորգ Հակոբյան
[1]Հոդվածը չծանրացնելու համար լոգարիթմների աղյուսակը չենք բերում: Այն հեշտությամբ կարելի է գտնել համացանցում:

