Քվանտային ֆիզիկայի 125-ամյակի և քվանտային մեխանիկայի 100-ամյակի առթիվ, Քվանտ, 2025, համար 5
Տեսական ֆիզիկայում այդ էֆեկտը սովորաբար անվանում են թունելային։ Թունելային էֆեկտի հանրագիտարանային սահմանումը հետևյալն է՝ միկրոմասնիկի ներթափանցումը պոտենցիալ արգելքի շրջան, երբ մասնիկի ընդհանուր մեխանիկական էներգիան փոքր է պոտենցիալային արգելքի բարձրությունից։
Միաչափ դեպքում, երբ էներգիայի կախվածությունը կոորդինատից ներկայացվում է գրաֆիկով, այն արտահայտվում է այնպես, կարծես մասնիկի ճանապարհին «լեռ» է, որը մասնիկը հաղթահարում է «թունելի» միջոցով՝ անցնելով այդ լեռան միջով և հայտնվելով մյուս լանջին։ Իրականում, իհարկե, ոչ մի լեռ չկա։ Այն երևում է միայն գրաֆիկի վրա։ Իսկ փորձերի ժամանակ, որտեղ հայտնաբերվում է նման էֆեկտը, մասնիկը իր շարժման ընթացքում մոտենում է այն կետին, որտեղ նրա վրա ազդում է ետ շպրտող ուժ, և դասական ֆիզիկայի օրենքների համաձայն՝ կանգ է առնում, ապա փոխում իր արագության նշանը։ Մի խոսքով, մասնիկը անդրադարձվում է կարծես մի անտեսանելի պատից։ Գիտաֆանտաստիկ գրողներն այս անտեսանելի պատը անվանել են ուժային արգելք։
Բայց պարզվեց, որ միկրոաշխարհում այդպես չէ, ավելի ճիշտ՝ միանգամայն այդպես չէ։ Այդ իրավիճակում միկրոմասնիկների հոսքն այնպես է իրեն պահում, որ հոսքի մի մասն իրականում անդրադառնում է։ Սակայն հոսքի մի մասը ինչ-որ առեղծվածային ձևով հայտնվում է ուժային արգելքի տարածքում և նույնիսկ արգելքի հետևում, եթե այն ունի վերջավոր երկարություն։ Հատկապես արտասովոր է մասնիկների վիճակը հենց այդ արգելքի հատվածում։
Միկրոֆիզիկայում ավելի նպատակահարմար է ուժային արգելքը դիտարկել որպես պոտենցյալ արգելք, այսինքն՝ մասնիկի պոտենցյալ էներգիայի այնպիսի կախվածություն հեռավորությունից, որը համապատասխանում է այն ուժերին, որոնք նրան թույլ չեն տալիս ներթափանցել արգելքի տարածք։ Եթե E-ն լրիվ մեխանիկական էներգիան է, ապա պահպանման օրենքի համաձայն այն նույնն է արգելապատնեշից առաջ և արգելապատնեշի հետևում, իսկ U0-ն ուղղանկյուն արգելապատնեշի բարձրությունն է, այսինքն՝ մասնիկի փոխազդեցության պոտենցիալ էներգիայի արժեքը արգելապատնեշի տարածքում գործող ուժերի հետ, ապա մասնիկի կինետիկ էներգիան արգելապատնեշի տարածքում Eկ= E-U0 է։ Եվ եթե U0>E, ապա Eկ<0՝ կինետիկ էներգիան բացասական է, իսկ արագությունը՝ կեղծ։ Ինչպե՞ս կարելի է դա պատկերացնել։
Ինչպես ընդունված է ժամանակակից միկրոֆիզիկայում՝ զուտ վիրտուալ, այսինքն՝ առանց այս տարածքում մասնիկի վարքագծի որևէ իրական (տեսողական) պատկեր փնտրելու։ Այս դեպքում, եթե արգելքը վերջավոր երկարություն ունի, այն կոչվում է արգելքի լայնություն, ապա արգելքի հետևում մասնիկը մտնում է մի տարածք, որտեղ կրկին նրա լրիվ էներգիան մեծ է պոտենցիալից, իսկ կինետիկ էներգիան՝ դրական։ Մասնիկը «նորից իրականանում է» և շարունակում է իր շարժումը։
կրկին նրա լրիվ էներգիան մեծ է պոտենցիալից, իսկ կինետիկ էներգիան՝ դրական։ Մասնիկը «նորից իրականանում է» և շարունակում է իր շարժումը։

Մասնիկների հոսքի առումով սա նշանակում է, որ հոսքի մի մասը չի անդրադարձել, այլ անցել է արգելքի միջով՝ կարծես երևակայական թունելով։ Այստեղից էլ առաջացել են «թունելային էֆեկտ», «թունելացում» տերմինները։ Իսկ առանձին մասնիկի նկատմամբ մաթեմատիկական ձևակերպումը հնարավորություն է տալիս սահմանել արգելքը հաղթահարելու հավանականությունը, որը հաշվվում է որպես արգելքը անցած մասնիկների թվի N հարաբերությունը արգելքին մոտեցած մասնիկների թվին N (այսինքն՝ W= N/ N) Այս հավանականությունը հաճախ անվանում են արգելքի թափանցելիության գործակից։
Ոչ մի փորձարարական եղանակ չկա, որով հնարավոր լինի հետևել առանձին մասնիկի շարժմանն արգելքի շրջանում, օրինակ՝ հետևել նրա հետագծին։
Եվ դասական ֆիզիկայում թունելային էֆեկտի համար բացատրություն ուղղակի չկա։ Այստեղ «բացատրություն» ասելով նկատի է առնվում որևէ պատկերավոր մոդելի ստեղծում և վերլուծություն։ Բայց փաստը մնում է փաստ․ այդ երևույթը իրականում գոյություն ունի։ Այն նկատել են և սկսել ուսումնասիրել անկախ քվանտային ֆիզիկայի ձևավորումից։ 20-րդ դարի սկզբին, երբ արագ զարգանում էր ռադիոէլեկտրոնիկան, ֆիզիկոսները մեծ ուշադրություն էին դարձնում գազային պարպումների մանրամասն ուսումնասիրությանը։ Եվ 1901 թվականին՝ Քեմբրիջում՝ Ջ.Ջ. Թոմսոնի լաբորատորիայում, երիտասարդ գիտնական Ռոբերտ Էրհարտը երկու մոտ կանգնած էլեկտրոդների միջև գազային պարպումները ուսումնասիրելիս ստացավ իոնների վարքի անսպասելի արդյունքներ։ Թոմսոնը ենթադրեց, որ սա փորձի սխալ չէ, այլ՝ նոր ֆիզիկական երևույթ։
Ռադիոլամպերի ստեղծմանն ուղղված պրակտիկ աշխատանքները շեղեցին ֆիզիկոսների ուշադրությունն այդ անհասկանալի երևույթի հետազոտությունից։ Միայն 1911թ․ Թոմսոնի ասպիրանտ Ֆրանց Ռոզերը շարունակեց հետազոտությունները։ 1914 թվականին նա հայտնաբերեց կատոդից էլեկտրոնների արտանետում (էմիսիա), երբ արտանետումը չէր կարող տեղի ունենալ մոտիկ տեղակայված մեկ այլ բացասական լիցքավորված էլեկտրոդի առկայության պատճառով (խորը վակուումի պայմաններում): Այս երևույթը անվանվեց ավտոէմիսիա, սակայն այն ժամանակ դրան բացատրություն չտրվեց։ Այդ ժամանակ Կավենդիշի լաբորատորիայի ֆիզիկոսները մեծ ոգևորությամբ զբաղվում էին ատոմի պլանետար մոդելի մշակմամբ և առաջին միջուկային ռեակցիաներով։ Սակայն միջուկային ֆիզիկայում նույնպես կային անբացատրելի երևույթներ։ Դրանցից մեկը միջուկների ռադիոակտիվ ձևափոխումների հավանականային բնույթն էր։
Այս անհասկանալի երևույթների տեսական բացատրությունը, որը կապված էր պոտենցիալ արգելքի գոյության հետ, հայտնվեց միայն քվանտային մեխանիկայի ստեղծումից հետո՝ 1925 թվականին։ Գերմանացի ֆիզիկոս Ֆրիդրիխ Հունդը, խորհրդային ֆիզիկոսներ Լեոնիդ Մանդելշտամը, Միխայիլ Լեոնտովիչը և Գեորգի Գամովը, ինչպես նաև ամերիկացի ֆիզիկոսներ Ռոնալդ Գյունրին ու Էդվարդ Կոնդոնը՝ գրեթե միաժամանակ և անկախ միմյանցից, պոտենցիալ արգելքներով խնդիրների համար կիրառեցին Էրվին Շրեդինգերի նոր ստեղծած ալիքային քվանտային մեխանիկան։ Իսկ մատրիցային քվանտային մեխանիկայի ստեղծող Մաքս Բորնը ընդհանրացրեց բոլոր այդ հետազոտությունները՝ մշակելով քվանտային թունելացման ընդհանուր տեսությունը։
Այս դիտարկումներում և տեսություններում գլխավորը հիմնարար մերժումն էր երևույթի տեսողական մեխանիզմի որոնման, և այն հարցի պատասխանի, թե ինչ է տեղի ունենում միկրոմասնիկի հետ պոտենցիալ արգելքի տարածքում։ Քվանտային մեխանիկայի հիմնարար դրույթներից մեկն անորոշության սկզբունքն է (անորոշությունների հարաբերակցությունը)։ Այս սկզբունքի համաձայն՝ որքան որոշակի է դառնում միկրոմասնիկի դիրքը, այնքան անորոշ է դառնում նրա իմպուլսը (արագությունը)։ Այդ պատճառով էլ պոտենցիալ արգելքի տարածքում մասնիկի վարքագծի վերաբերյալ դասական դատողությունը (տրված է հոդվածի սկզբում) կիրառելի չեն միկրոաշխարհի մեխանիկայի (քվանտային մեխանիկայի) համար։ Անհնար է տարբերակել պոտենցիալ և կինետիկ էներգիաները ընդհանուր էներգիայի մեջ, դրանք սահմանված չեն արգելքի տիրույթում։ Չէ՞ որ կինետիկ էներգիան արագության ֆունկցիա է, իսկ պոտենցիալ էներգիան՝ կոորդինատի։ Իսկ կոորդինատն ու արագությունը կապված են անորոշության հարաբերակցությամբ։ Այս ամենը սահմանափակում է մասնիկի վարքի որևէ տեսանելի կամ պատկերավոր մոդելի որոնումը պոտենցիալ արգելքի տիրույթում, օրինակ՝ նրա շարժման հետագիծը։ (Այստեղ որոշակի նմանություն կա այն փաստի հետ, որ էլեկտրոնի շարժման հետագիծը, որպես այդպիսին, չի սահմանվում ատոմի ներսում։)
Թունելավորման բոլոր փորձերի արդյունքները ոչ թե մասնիկի վարքագծի բնույթի ուսումնասիրությունն են արգելքի տարածքում, այլ արգելքի «թափանցիկության» փաստը և թափանցիկության գործակցի չափումը։ Եվ տեսական աշխատանքների նպատակն է այդ գործակցի հաշվարկային սահմանումը։ Այս տեսական ուսումնասիրություններում ամենաարդյունավետը եղավ ալիքային քվանտային մեխանիկայի կիրառումը(մասնավորապես՝ Շրյոդինգերի հավասարման կիրառումը), որը ձևավորվեց 1925 թվականին։
Շրյոդինգերի հավասարում
Մաթեմատիկորեն այս հավասարումը պատկանում է դիֆերենցիալ ալիքային հավասարումների դասին, այսինքն՝ դրա լուծումը պետք է լինի ալիքային հավասարում, օրինակ՝ կոորդինատների և ժամանակի եռանկյունաչափական ֆունկցիաների տեսքով (հիշե՛ք ձայնային կամ էլեկտրամագնիսական ալիքի հավասարումը): Այստեղ չենք գրի համապատասխան դիֆերենցիալ հավասարումը, քանի որ դա արդեն շատ լավ արված է դասագրքերում և բազմաթիվ կայքերում՝ «Շրյոդինգերի հավասարում» վերնագրով։

Նշենք միայն, որ այդ հավասարումը պարունակում է առաջին կարգի ածանցյալն ըստ ժամանակի և երկրորդ կարգի ածանցյալներ ըստ կոորդինատների։ Այս հավասարման լուծումը նշանակում է կատարել դիֆերենցման հակադարձ գործողություն, այսինքն՝ ինտեգրում։
Այս հավասարման «քվանտայինությունն» այն է, որ ունի լուծումներ միայն մասնիկի ամբողջական էներգիայի որոշակի (թույլատրելի) արժեքների դեպքում։ Այդ էներգիան «ավտոմատ կերպով» քվանտացվում է։ Իսկ միկրոմասնիկի վրա գործող ազդեցությունը պարզ միաչափ խնդիրներում տրվում է պոտենցիալ էներգիայի ֆունկցիայով՝ կախված կոորդինատից։
Բայց ի՞նչն է հանդիսանում այս հավասարման կամ նրա լուծման մեջ ֆունկցիան, այլ կերպ ասած՝ ի՞նչն է տատանվում այն ալիքի մեջ, որի հավասարումը հենց Շրյոդինգերի ալիքային հավասարման լուծումն է։ Եվ առհասարակ՝ ինչո՞ւ է միկրոմասնիկների հավասարման մեջ խոսքը գնում ալիքի մասին։

Քվանտային մեխանիկայի սկիզբն հանդիսացավ Լուի դը Բրոյլի հիպոթեզը նյութի ալիքային հատկությունների մասին, որը նա առաջարկեց 1923 թվականին։ Այդ ժամանակ արդեն լայն ընդունելություն էր գտել 1905 թվականին Այնշտայնի կողմից առաջադրված հիպոթեզը ճառագայթման քվանտային հատկությունների մասին, որը փայլուն կերպով կիրառեց Արթուր Կոմպտոնը՝ բացատրելու համար էլեկտրամագնիսական ճառագայթման և ազատ էլեկտրոնների փոխազդեցությունը։
Այս հիպոթեզի համաձայն՝ էլեկտրամագնիսական ալիքները կարելի է դիտարկել նաև որպես մասնիկներ (կորպուսկուլներ), որոնք ունեն մեխանիկական քվանտային բնութագրեր՝ իմպուլս p և էներգիա E, որոնք կապված են ալիքի երկարության հետ հետևյալ հարաբերություններով՝ p=h/λ, E=hc/ λ, որտեղ h-ը Պլանկի հաստատունն է, c-ն՝ լույսի արագությունը վակուումում։
Այսպիսով, էլեկտրամագնիսական ճառագայթումն ունի երկակի բնույթ (դուալիզմ)։ Որոշ երևույթներում ավելի էական են ալիքային հատկությունները, իսկ մյուսներում՝ կորպուսկուլային (քվանտային)։ Բայց այն, որ նման դուալիզմը հատուկ է ոչ միայն էլեկտրամագնիսական ճառագայթմանը, այլ նաև յուրաքանչյուր նյութական օբյեկտի, ֆիզիկոսների կողմից ընդունվեց ոչ միանագամից։
Սա հենց դը Բրոյլի հիպոթեզի էությունն է ։ Ցանկացած օբյեկտ, որն ունի իմպուլս p, միևնույն ժամանակ ունի նաև որոշ ալիքային հատկություններ, որոնք բնութագրվում են ալիքի երկարությամբ՝ λ = h/p։
Եվ իսկապես, Բրոյլի հոդվածի հրապարակումից և 1924 թվականին այդ թեմայով դիսերտացիայի պաշտպանությունից հետո, ամերիկացի ֆիզիկոսներ Ջոզեֆ Դևիսոնը և Լեսթեր Ջերմերը 1925 թվականին իրենց փորձերում հայտնաբերեցին էլեկտրոնների դիֆրակցիան բյուրեղներում։ 1930 թվականին այդ երևույթը ավելի մանրամասն ուսումնասիրեց բրիտանացի ֆիզիկոս Ջորջ Թոմսոնը, ով 1897 թվականին էլեկտրոնը «հայտնաբերող» նշանավոր Ջ․Ջ․ Թոմսոնի որդին էր։ Սկսվեց էլեկտրոնային միկրոսկոպիայի դարաշրջանը։ Ջոզեֆ Դևիսոնը և Ջորջ Թոմսոնը 1937 թվականին դարձան Նոբելյան մրցանակակիրներ։ Նշենք նաև, որ Ջ․Ջ․ Թոմսոն ավագը ոչ միայն գերազանց ֆիզիկոս էր, այլև հիանալի մանկավարժ։ Լինելով Նոբելյան մրցանակակիր (1906թ.)՝ նա դաստիարակեց յոթ Նոբելյան մրցանակակիր, այդ թվում՝ իր որդուն։
Բայց 1924 թվականին ֆիզիկոսներից քչերն էին հետաքրքրված դուալիզմի խնդրով։ Այդ հարցով հետաքրքրվողների մեկն էր Ցյուրիխի համալսարանի տեսական ֆիզիկայի պրոֆեսոր Էրվին Շրյոդինգերը։ Նրան հետաքրքիր թվաց դը Բրոյլի այն գաղափարը, որը վերջինս ներկայացրել էր իր դիսերտացիայում, ըստ որի՝ ատոմում կայուն ուղեծրի վրա էլեկտրոնի շարժման հետագիծը կարելի է պատկերացնել որպես որոշակի կանգուն ալիք։ Օգտագործելով կանգուն ալիքի ստացիոնարության պայմանը էլեկտրոնի ուղեծրի երկայնքով և իր իսկ առաջարկած էլեկտրոնի ալիքային հատկությունների պոստուլատը՝ դը Բրոյլը ստացավ ջրածնի ատոմի համար էլեկտրոնի էներգիայի հենց այն քանակական (դիսկրետ) արժեքները, որոնք դեռ 10 տարի առաջ ստացել էր Նիլս Բորը իր տեսությունում, և որոնք փորձով շատ լավ հաստատված էին։
Շրեդինգերը սկսեց որոնել այնպիսի հավասարում, որի լուծումը հենց այդ կանգուն ալիքը կլիներ։ Սակայն դա հեշտ խնդիր չէր։ Սկզբում նա անհաջողություն ունեցավ՝ փորձելով կանգուն ալիքը պատկերացնել որպես էլեկտրոնի լիցքի տարածական ալիքաձև բաշխում:
1925 թվականի աշնանը Շրյոդինգերի տուբերկուլյոզը սրացավ, և նա մեկնեց բուժվելու ամենահայտնի ալպյան առողջարաններից մեկում՝ Արոզա առողջարանում։ Շրյոդինգերի կենսագրություններում երբեմն գրում են, թե նա ապրում էր «լեռնային խրճիթում»։ Այդպես է նկարագրվում միջնադարյան ճգնավորի կերպարը։ Բայց իրականում ոչ մի նման բան չի եղել։ Խրճիթ չէր, այլ՝ հարմարավետ լեռնատնակ։ Ճգնում էր ոչ թե միայնակ, այլ մի երիտասարդ կնոջ հետ, որը նույնիսկ ֆիզիկայից ինչ-որ բան էր հասկանում։ Մի խոսքով՝ ստեղծված էին բոլոր պայմանները և՛ աշխատանքի, և՛ հանգստի համար։ Հենց այնտեղ էլ Շրեդինգերը ստեղծեց իր հռչակավոր հավասարումը, որը նշանավորեց նոր տեսության՝ «ատոմների և մոլեկուլների մեխանիկայի ալիքային տեսության» ծնունդը։ Նրա տեսության առաջին ստուգումը նունպես եղավ ջրածնի ատոմի սպեկտրի վերաբերյալ փորձարարական տվյալների հետ համեմատությունը։ Եվ սա պարզապես տեսության ու փորձի համեմատություն չէր։ Տեսությունը կանխատեսում էր ավելի ճշգրիտ արժեքներ, որոնք հետագայում հաստատվեցին փորձով։ Հաջողությունից ոգևորված՝ Շրյոդինգերը իր աշխատանքի արդյունքների մասին հոդված ուղարկեց գերմանական ֆիզիկական ամսագրին, որը հրապարակվեց 1926 թվականին։
Իսկ ի՞նչն է տատանվում դե Բրոյլի ալիքում։ Շրյոդինգերը հրաժարվեց այս տատանվող օբյեկտի տեսողական պատկերի որոնումներից։ Նա պարզապես անվանեց այն՝ ընտրելով հունարեն տառ, որը նախկինում չէր օգտագործվել ֆիզիկայում՝ ψ (պսի) տառը։ Այսպիսով, դե Բրոյլի ալիքում տատանվում է ψ-ֆունկցիան։ Հետևաբար, հենց այդ ֆունկցիան է դառնում Շրեդինգերի հավասարման փաստարկը։
Նույն ժամանակաշրջանում գերմանացի տեսական ֆիզիկոսները Վերներ Հեյզենբերգի և Մաքս Բորնի գլխավորությամբ մշակեցին մի տեսություն, որը անվանեցին մատրիցային քվանտային մեխանիկա։ Շրյոդինգերը ապացուցեց, որ իր տեսությունը տալիս է նույն արդյունքները, ինչ այդ մատրիցային տեսությունը։ Այդ ժամանակվանից ի վեր Շրյոդինգերի հավասարումը համարվում է ալիքային քվանտային մեխանիկայի հիմնական բովանդակությունը։
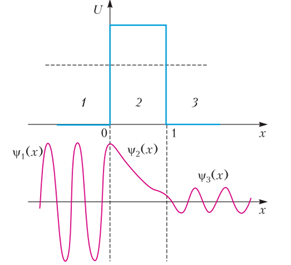
Որոշ ժամանակ անց, Նիլս Բորի ազդեցության տակ, ψ ֆունկցիային տրվեց հավանակության տեսության նշանակություն։ Քանի որ այն, որպես դիֆերենցիալ ալիքային հավասարման լուծում, կոմպլեքս մեծություն է, իսկ W հավանականությունը՝ իրական մեծություն, ապա ψ ֆունկցիայի «ֆիզիկականացումը» հետևյալն է՝ ψ Ֆունկցիայի մոդուլի քառակուսին տվյալ կետում և տվյալ պահին մասնիկի գտնվելու հավանականության խտությունն է։ ψ ֆունկցիայի հավանական մեկնաբանությունը թույլ է տալիս նշել սահմանային և սկզբնական պայմանները, որպեսզի այն որոշվի որպես Շրյոդինգերի հավասարման լուծում։ Այստեղ ներկայացված գրաֆիկներից մեկը ցույց է տալիս լուծումը ամենապարզ դեպքում՝ ψ1 և ψ2 ֆունկցիաները արգելքից առաջ և հետո, ինչպես նաև արգելքի ներսում գտնվող տիրույթների համար։ x2 և x1 կետերում գտնվող ψ ֆունկցիաների քառակուսիների հարաբերությունը պոտենցիալ արգելքի թափանցիկության գործակիցն է։
Այսպիսով, թունելային էֆեկտн այն երևույթներից է, որը հաջողվեց բացատրել և հաշվարկել միայն քվանտային մեխանիկայի օգնությամբ, ավելի ճիշտ՝ ալիքային քվանտային մեխանիկայի օգնությամբ, այսինքն՝ Շրյոդինգերի հավասարման միջոցով։ Ցուցադրենք այն միջուկային ֆիզիկայի օրինակներով։

Շարունակությունը՝ այստեղ։
Թարգմանությունը՝ Իննա Իսրայելյանի
Հեղինակ՝ Լ․ Բելոպուխով

