Թվերի ընտրության և թվաբանական խնդիրների կազմության սկզբունքները

§3. Խնդրի ֆաբուլան և թվային տվյալների ընտրությունը

Սկսենք այն հարցից, որի լուծման քարացվածությունը  գործնականում աչքի է ընկնում առանձնահատուկ ցայտունությամբ, և որի համար համեմատաբար հեշտ է ասելը, թե ինչ է անհրաժեշտ ձեռնարկել: Նկատի ունենք խնդրի ֆաբուլան կամ ձևակերպումը, հարցադրման բնականությունը և թվային տվյալների ընտրությունը: Ընդունված է համարել, որ այս ամենն ունի երկրորդական նշանակություն, որ հարցի էությունը խնդրի թվաբանական բովանդակությունն է, երևակայության այն ջանքերը, տրամաբանական դատողությունների այն գործընթացը, այն թվային հաշվարկները, որոնք առաջարկվում են սովորողին, այլ ոչ թե խնդրի բովանդակության իրական լինելը: Նույնիսկ եթե այս դրույթհետ կարելի լիներ համաձայնել, ամեն դեպքում հենց նոր արտահայտված պնդումները բավարար հիմք չեն, որպեսզի անտեսվի խնդրի ֆաբուլայի մասին ցանկացած մտահոգութունը: Ֆաբուլայի մասին մտահոգության անտեսումն ի վերջո բերում է խնդիրը արհեստական, երբեմն պարզապես ծիծաղելի, զուտ արտաքին նշաններով իրական կմախք ունեցող պայմաններով ծանրաբեռնելուն: Ամենավատն այն է, որ խնդիրների առատությունը, որոնք ուսուցման տարիների ընթացքում սովորողներին ստիպում են ծամծմել նույն ավանդական նյութը, անխուսափելիորեն ձանձրույթ են տարածում, որն էլ վերաճում է  թվաբանության նկատմամբ հակակրանքի, հատկապես, եթե ուսուցումը էականորեն հանգում է սովորողներին  բաղադրատոմսեր և թվաբանական հաշվապահության բյուրոկրատական կանոններ պարտադրելուն:

Այստեղ անհրաժեշտ է նշել, որ  չենք պատրաստվում ընդհանրապես հրաժարվել հայտնի թվաբանական խնդիրների տեսակներից (խնդիրներ միմյանց ընդառաջ և նույն ուղղությամբ գնացող ճամապարհորդներով ու գնացքներով, խնդիրներ «լողավազանների», «խառնուրդների» ամսին և այլն): Այս դասական խնդիրները բավական տեսանելի և հարմար սխեմաներ են այն թվաբանական իրավիճակների, որոնցում սովորողը պետք է կողմնորոշվի: Բայց չի կարելի սահմանափակվել այս խնդիր-սխեմաներով և պտտվել արագորեն ձանձրացնող թեմաների շրջանում: Այլ կերպ չենք կարող խուսափել հարցի արհեստական դրվածքից և նույն շարժառիթի ձանձրալի կրկնությունից: Մյուս կողմից, խնդիրների թեմաների և ձևակերպումների մեջ բազմազանություն մտցնելով և ձգտելով խդրում օգտագործովող տվյալների և անհայտների միջև առնչությունները  հնարավորին չափ իրականին մոտեցնելու և համապատասխան թվային տվյալներ ընտրելու` չի կարելի, իհարկե, ծայրահեղության մեջ ընկնել և խնդրի տեքստը ծանրաբեռնել այնպիսի տեխնիկական և վիճակագրական տվյալներով, որոնք սովորոների համար ավելորդ դժվարություն կառաջացնեն: Բայց այս վերջին վտանգն առաջինից փոքր է. «նվազագույն դիմադրության» գիծն հենց այնտեղ է, այլ ոչ այստեղ: Եթե հնարավոր չէ անհրաժեշտ թվաբանական խնդիրների բովանդակությունը հրամցնել հնարավոր կենդանի տեսքով, ընտրել հետաքրքիր, կոնկրետ և դրա հետ մեկտեղ սովորողներին հասանելի ձևակերպում, ինչ մտավոր վարժանքի և թվաբանական հմտությունների դաստիարակության առումով հասանելի կդարձնի անհրաժեշտ նպատակները, այն ժամանակ, իհարկե, ստիպված պետք է համակերպվել դրա հետ:

Բայց ամբողջ հարցն այն է, որ համարյա միշտ այդպիսի ձևակերպում հնարավոր է գտնել, և  դա չի արվում միայն այն պատճառով, որ ավելի  հեշտ է խնդրի պայմանը արտագրել ավելի վաղ կազմված ժողովածուներից՝ մի քիչ դրանք ժամանակակից դարձնելով, քան մտածել այն մասին, ինչպես խնդիր կազմել՝ պահպանելով նշված պահանջները: Դեռ չեմ խոսում նրանից, որ ժողովածուներ կազմողները պետքական թվաբանական բովանդակության մասին էլ հաճախ այնքան էլ մտածում:

Պատկերավորության համար մեզ մոտ կիրառվող ժողավածուներից ընտրված մի քանի օրինակ բերենք:
«Տնտեսուհուն 73/8 ռուբլի ուներ»: «Վաճառվել է  317/19 կգ շաքարավազ՝ կիլոգրամը  21/7 ռուբլով»: «Նապաստակը  1,35 ժամում վազում է 14,13855կմ»: Թվային տվյալների ծիծաղելի ընտրությունը մեկնաբանության կարիք չունի: Եվ այսպիսի խնդիրները հազվադեպ չեն: Ժողովածուներ կազմողները հաճախ արդարանում են, որ «այլ կերպ դժվար է սովորական և տասնորդական կոտորակներով գործողություն պահանջող խնդիրներ կազմելը»: Նույնիսկ եթե դա այդպես է, ապա այդպիսի փաստարկն ընդունելի կլինի նրանց շուրթերից, ովքեր խնդիրների ժողովածուներ չեն կազմում:

Դիտարկենք խնդիրներ, որոնք չեն պարունակում այդպիսի աչքի ընկնող անհեթեթություններ և ներկայանում են բավականաչափ սովորական:

«Երեք պուրակում  4160 կեչի կա: Քանի՞ կեչի կա յուրաքանչյուր պուրակում, եթե առաջինում 3 անգամ շատ կա, քան երկրորդում, իսկ երրորդում այնքան, որքան առաջինում և երկրորդում միասին»:

Կարծես առարկելու բան չկա: Բայց այնուամենայնիվ՝ այդ ի՞նչ տարօրինակ պուրակներ են, կեչիների այդպիսի ճշգրիտ թվային հարաբերակցությամբ: Մի՞թե պարզ չէ, որ յուրաքանչյուր պուրակի կեչիների թիվը նախօրոք պետք է հաշված լինեին, քանի որ այլ կերպ կեչիների քանակը համեմատել չէր լինի: Ի վերջո բոլորովին անիրական, եթե մտածես ուղղակի զավեշտալի հարցադրում է, որը չի կարող պատասխանի նկատմամբ որևէ հետաքրքրություն առաջացնել:

«Երկու բիդոն ունեն 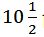 լիտր տարողություն: Եթե առաջին բիդոնի տարողությունը երկու անգամ ավելի լիներ, իսկ երկրորդինը՝  8 լիտրով, քան իրականում, երկուսի ընդհանուր տարողությունը կկրկնապատկվեր: Որքա՞ն է յուրաքանչյուրի տարողությունը»:

Մենք հատուկ ենք առաջին հայացքից անմեղ խնդիրներ բերում: Բոլորն այնքան են սովորել  անիմաստ և ձանձրալի տեքստերին, որ հակված չեն այդպիսի խնդիրների մեջ  դատապարտելի բան տեսնելու: Բայց ուշադիր նայեք: Ինչո՞վ է հիմնավորված խնդրի պայմանը: Ինչո՞ւ է այդպես: Ինչո՞ւ հենց երկու անգամ ավելի: Ինչո՞ւ կկրկնապատկվի: Իրական ի՞նչ հանգամանքներում կարող է այդպիսի խնդիր լուծելու անհրաժեշտություն առաջանալ:

«1365 գիրքը կազմում է  դպրոցական գրադարանի բոլոր գրքերի 35%-ը: Գրադարանի բոլոր գրքերը դասավորված են երեք պահարաններում, ընդ որում նրանցում գրքերի քանակները հարաբերում են, ինչպես 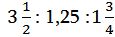: Քանի՞ գիրք կա յուրաքանչյուր պահարանում»:

Հետաքրքիր և իրական է, չէ՞:

«Դպրոցականը սկզբում իր գումարի 3/14-ը ծախսեց գրենական պիտույքներ գնելու համար, հետո մնացածի 5/11-ը՝ դասագրքեր գնելու համար, և նրա մոտ մնաց երկու գնումների ժամանակ ծախսածից չորս դրամ քիչ: Սկզբում որքա՞ն գումար կար դպրոցականի մոտ»:

Միայն ձևակերպումը ինչ ասես արժե:

«Կոլտնտեսությունից դեպի 48 կմ հեռավորության վրա գտնվող քաղաք միաժամանակ դուրս եկան գյուղացին՝ ձիով,  7 կմ/ժ արագությամբ, և նամակատարը՝ հեծանվով, 13 կմ/ժ արագությամբ: Քանի՞ ժամ հետո մինչև քաղաք նամակատարին կմնա անցնելու 3 անգամ քիչ, քան գյուղացուն»:

Դժվար է պատկերացնելը, թե ինչով կարող է պայմանավորված լինել խնդրի պատասխանը ստանալու հետաքրքրությունը: Թեմատիկան միայն արտաքուստ է արդիական: Նույն  հիմնավորմամբ կարելի էր ասպետին ձիով  և սուրհանդակին վազքով ուղարկել. ձևակերպումը գուցե երեխաների համար ավելի զվարճալի կիներ, սակայն հարցադրումը դրանից չէր լավանա: Եվ հարյուրներով նմանատիպ խնդիրներ կան, ու երեխաներին տարիներ շարունակ պահում են այսպիսի «թվաբանական դիետայի» վրա:

Պետք է խոստովանել, որ անցյալում խնդրագրքերի հեղինակները ավելի շատ էին հոգ տանում խնդիրների պայմանների իրական լինելու և իմաստալից հարցադրումների համար: Դասական խնդիրների` եկամուտ ստանալու նպատակով գինիները խառնող վաճառականների վերաբերյալ, սուրհանդակների ու ճանապարհորդների մասին, փողոցը հավասարաչափ սալարկող հողափորի և բանվորի մասին հարցերը, որոնցից հիմա նույնիսկ որոշակի ռոմանտիկա է բուրում, իսկապես, ժամանակին իրականությունն են արտացոլել:

Թե խնդիրների պայմանները որքան իրական են ներկայացնել նախկին հեղինակները, փաստում են հետևյալ օրինակները, որոնք վերցված են XIX դարի սկզբի հանրահաշվի ուղեցույցից:

«Նավակը Նևայով Կադետական մասնաշենքից մինչև Զինապալատ 48 րոպեում է գնում, և վերադառնում 32 րոպեում. ընդ որում թիավարները թիավարում էին նույն ուժգնությամբ. հարցն այն է, թե քանի  սաժենի է հավասար Նևայի հոսանքը մեկ րոպեում, և նավակը նույն ժամանակում քանի սաժեն կանցնի կանգնած ջրում»:

Հեղինակը նույնիսկ անհրաժեշտ չի համարում Կադետական  մասնաշենքից մինչև Զինապալատ  եղած հեռավորությունը նշելու, միայն լուծման մեջ օգտագործվում է, որպես հայտնի փաստ, որ այդ հեռավորությունը «1536 սաժեն» է: Ժամանակակից խնդրագրքերում նման «վրիպում» հազիվ թե հնարավոր լինի:

«Տարիքի վերաբերյալ հարցին մի տիկին պատասխանեց՝ իմ տարիքն այնպիսին է, որ եթե այն քառակուսի բարձրացնեք կամ բազմապատկեք 53-ով  և արդյունքից հանենք  696, կստանանք նույն թիվը»:

Պայմանը, իհարկե, այնքան էլ իրական չէ, բայց ինչպե՞ս է դրան վերաբերվում հեղինակը:

Լուծելով քառակուսի հավասարումը` նա նկատում է. «քանի որ հարցը վերաբերում է կնոջ տարիքին, քաղաքավարությունից ելնելով, պետք է արմատի նշանից առաջ վերցնել բացասական նշանը»:

Ահա մի քանի խնդիր 1868 թվականի ժողովածուից:

«Դեղատանը պատվիրել են ատամի փոշի հետևյալ բաղադրությամբ` 2 դրախմ մանրացրած կարմիր սանդալենուն ավելացնել   մեկ սկրուպուլ 10 գրան մանրացրած շիբ, 4  դրախմ մանրացված տենդի տերև մեկ կաթիլ կիտրոնի և մեկ կաթիլ մեխակի յուղ: Սխալմամբ դեղատան աշակերտը վերցրեց 2 կաթիլ կիտրոնի յուղ և 2 սկրուպուլ 8 գրան  շիբ: Ստացված զանգվածին նշված հավելանյութերից յուրաքանչյուրից  որքա՞ն պետք է խառնել, որպեսզի պահպանվի համապատասխան հարաբերությունը»:

Այստեղ էլ հարցադրումը լրիվ իրական է: Ճիշտ է «դրախմները», թերևս արդեն պետք չեն, բայց այն, որ սովորողներին չեն ծանոթացնում չափման ոչ մի ուրիշ միավորի հետ, բացի մետրային համակարգից, ուղղակի անհեթեթություն է: Մինչդեռ թերթերում կարելի է հանդիպել յարդ, մղոն և ուրիշ անվանումներ, և սովորողներին շատ օգտակար է այդ չափման միավորները մետրայինի վերածելու հմտություն ձեռք բերելը, և, ի դեպ, գործնականում տեսնելը մետրային համակարգի առավելությունը  նրանց համեմատ, որ մինչև այսօր օգտագործվում են Անգլիայում:

Երբ խնդրի հեղինակը իրականությունը նկատի ունի, նա չի վախենում մանրամասներից:

«Արևտրականը Բեռլինում նապաստակի 10 000 մորթի գնեց 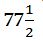 փութ քաշով` յուրաքանչյուր հազար հատի համար վճարելով 115 ռուբլի. դրանից բացի, յուրաքանչյուր փութի համար 2 ռուբլի 60 կոպեկ մաքսատուրք վճարեց, փաթեթավորելու և առաքելու համար յուքանչյուր 1000 ռուբլու համար վճարեց 6 ռուբլի, խոտանողին՝ յուրաքանչյուր 1000 ռուբլու համար` 4 ռուբլի, մինչև Կրոնշտադտ հասցնելու համար՝ 8 ռուբլի, նամակների առաքման համար՝ 7 ռուբլի 15 կոպեկ, մանր ծախսերի համար՝ 1 %, առևտրական միջնորդին՝ 2 %, մուրհակի և  դրոշմաթղթի համար՝ 5/8 %: Առևտրականը Բեռլինում քանի՞ թալեր է տալիս մորթու համար, եթե 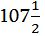թալերը հավասար է 100 ռուբլու»:

Ահա էլի մեկ խնդիր նույն ժողովածուից:

«Զարթուցիչով ժամացույցը, որը 12 ժամ 35 րոպեում 15 րոպե ետ է ընկնում, պետք է ստուգված ժամացույցով երեկոյան 10 անց 40 րոպե դնել այնպես, որ զարթուցիչը զնգա հաջորդ օրվա առավոտյան 4 անց 30 րոպե: Х թվից քանի՞ րոպե հետո պետք է  դնել րոպեների սլաքը, եթե զարթուցիչի ցուցիչը դրված է  4 անց 30 րոպեի վրա»:

Մյուս խնդիրներում օգտագործվում են տեղեկություններ նյութերի մասին, որոնք անհրաժեշտ են պատը նախաներկելու համար («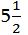 փութ կավճային լուծույթ, 1/5 փութ սոսինձ և 2/5 շտոֆ կաթ»), «երկաթաքարի, կարմիր և ալ աղյուսի»  «հումքից» ստացվածի մասին, հիմքը գցելու համար օգտագործվող նյութերի մասին  (յուրաքանչյուր խորանարդ սաժենի համար 3540 աղյուս՝ 1/20–ի չափով  հավելումով) և այլն:

Թեմատիկայի իրական լինելու հարցում պակաս հոգատարություն չի ցուցաբերել  Վորոնովան իր «Թվաբանական խնդիրների ժողովածու»-ում (1876).

 «Որոշել սոճու չոր վառելափայտի սաժենի քաշը` իմանալով, որ թարմ սոճու ծառի քաշը կազմում է նույն ծավալի ջրի 90 %-ը, չոր սոճու քաշը թարմ սոճու քաշի 9/11   մասն է, մեկ խորանարդ սաժեն ջրի կշիռը 593 փութ է, վառելափայտի մեկ սաժենը հավասար է 1/4 խորանարդ սաժենի, իսկ փայտանյութը կոճղերի միջև բաց տարածությունների պատճառով զբաղեցնում է վառելափայտի զբաղեցրած տարածքի 14/27 մասը»:

 «Նիժնի Նովգորոդի գավառի  գյուղերից մեկում բնակիչների մեծ մասը զբաղվում է կացնի արտադրությամբ: Հաշվեք մեկ կացնից ստացված միջին եկամուտը, համարելով, որ նրա համար օգտագործվում է 1/20 փութ երկաթ, որ մեկ փութ երկաթը կռելու համար ծախսվում է մեկ քառորդ փութ ածուխ և 1/5 փութ պողպատ, ընդ որում երկաթի մեկ փութo գնում են 1 ռուբլի 50 կոպեկով, պողպատինը՝  3 ռուբլի 20 կոպեկով, ածուխ քառորդ փութը՝ 1 ռուբլի 25 կոպեկով, իսկ մեծածախ վաճառքի դեպքում կացնի միջին արժեքը 40 կոպեկ է»:

 «Վոլգոգրադի նահանգի Կադինսկի գավառում  խեժ ստանալու համար գյուղացիները մեկ կամ մի քանի վառարաններով գործարաններ են սարքում: Հաշվեք երկու վառարան ունեցող գործարանի տարեկան միջին եկամուտը, համարելով, որ վառարանը 4 կաթսա ունի, որոնցից յուրաքանչյուրն օրական 1/16 սաժեն ձյութափայտից (կեչու կոճղից) 3/4  փութ խեժ է  տալիս, ընդ որում  30 փութանոց տակառ խեժը թորելու համար օգտագործվում է 2 սայլաբեռ վառելափայտ, իսկ տեղական գներով, մեկ փութ խեժը 1 ռուբլի արժե, մեկ խորանարդ սաժեն ձյութափայտւ՝ 6 ռուբլի, մեկ սայլաբեռ վառելափայտը՝ 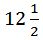կոպեկ»:

Իհարկե, հիմա էլ է հնարավոր  սովորողների թվաբանական ողջ անհրաժեշտ վարժանքը  կազմակերպել խնդիրներով, որոնք բավական իրական են, հետաքրքիր պայմաններ ու թվային տվյալներ ունեն, և այնպիսի հարցադրումներով, որ պատասխանը ստանալու նկատմամբ սովորողները զգայական առումով անտարբեր չլինեն: Մեզ շրջապատում են իրականության բազմազան և հետաքրքիր երևույթներ: Առարկաների և երևույթների փոխհարաբերությունները իրենց հետաքրքիր արտացոլումն են ստանում թվերում: Մի՞թե չի կարելի այդ հարուստ նյութից երեխաներին հասանելի և հետաքրքիր թվային տվյալներ առանձնացնել, դասավանդումն այնպես կառուցել, որպեսզի նրանց առաջ կամաց-կամաց բացվեն «թվային աշխարհի» նորանոր  էջեր՝ առաջարկվող առաջադրանքներում խելամտորեն օգտագործելով թվային տվյալները:
Այդ ուղղությամբ առաջին քայլը պետք է լինի համապատասխան տեղեկատուի ստեղծումը: Առաջին հերթին անհրաժեշտ է տրանսպորտի տարբեր տեսակներին առնչվող տեխնիկական տեղեկատվական գրականություն նայել (բոլոր թվային բնութագրերով՝ արագություն, բեռնատարողություն, չափեր, վառելանյութի սպառման նորմեր, մեքենայի հզորություն, ռեկորդային նվաճումներ և այլն), նյութեր հավաքել, մինչև անգամ համապատասխան օբյեկտների նկարներ, անվան, բնութագրող իրադարձությունների տեղի և ժամանակի  ճշգրիտ նշմամբ և այլն:

Այս աշխատանքում կարելի է մասնագետների ներգրավվել, որոնց համար այնքան էլ դժվար չէ ցույց տալ այն ամենը, ինչը կարող է օգտակար, հետաքրքիր և միաժամանակ դպրոցականին հասանելի լինել: Ոչ պակաս հարուստ նյութ կարելի է քաղել ֆիզիկական աշխարհագրությունից, ֆիզիկայից, քիմիայից, աստղագիտությունից, տնտեսական աշխարհագրությունից (չտարվել «չոր» թվային վիճակագրությամբ և պարզագույն զուգադրություններով, այլ ընտրել հետաքրքիր, թվային հորիզոնը ընդլայնող և երևակայության վրա ազդող տվյալներ), ժամանակակից տեխնոլոգիայից (հաճախ հանդիպող տարբեր նյութերի բաղադրությունը, նրանց ստացման եղանակները, տարբեր տեսակի վառելանյութերը, պողպատի տեսակները և այլն ): Արդիական է հեռավոր և ոչ վաղ անցյալի պատերազմերը ամենատարբեր կողմերից  բնութագրող առատ նյութը (զորքի կառուցվածք և թիվ, տեխնիկական  սարքավորումներ, շարժման արագություն, ծախսված նյութի քանակ և այլն):

Գործնական հետաքրքրություն կարող են ներկայացնել  իրականությանը համապատասխանող նախահաշվարկային բնույթի տվյալներով խնդիրները (տրակտորային պարկի, բեռնատար մեքենաների մատակարարման համար անհրաժեշտ վառելանյութի, նյութերի քանակի ու արժեքի և դրա առաքման և աշխատուժի վճարման հաշվարկ և այլն): Այս վերջին տեսակի խնդիրները պետք է որքան հնարավոր է ճշգրիտ արտացոլեն իրավիճակը՝ թվային տվյալներն ու մանրամասները կարող են ժամանակ առ ժամանակ և տեղից տեղ փոխվել: Այսպիսով, թվաբանական խնդիրների ֆաբուլային, հարցադրման իմաստալիցությանը  և թվային տվյալների ընտրությանը ներկայացվող պահանջները բավական որոշակի են: Ճանապարհը, որին հետևելով սովորական թերությունները կարելի է վերացնել, նույնպես բավական պարզ են, չնայած բավական ջանք և ժամանակ տանող աշխատանք է ենթադրվում: Իր բնույթով անհամեմատ ավելի դժվար է խնդիրների թվաբանական բովանդակության հարցը, որին մենք հիմա կանրադառնանք:

Հեղինակ՝ Իգոր Առնոլդ

Թարգմանիչ՝ Մանուշակ Աբրահամյան