Թվեր: Թվաբանությունից մինչև բարձրագույն մաթեմատիկա

Սկիզբը
Նախորդ հատվածը 

Գլուխ 3. Շրջանցելով «գումարում»-ը
Պլյուս ու բևեռ և պլյուս ու բևեռ

Պատկերացնենք, որ 1դյույմ կողմով քառակուսի ենք նկարել: Այդպիսի քառակուսին կարելի է անվանել քառակուսի դյույմ և օգտագործել որպես մակերեսի միավոր: Այժմ նկարենք 2 դյույմ կողմով քառակուսի, յուրաքանչյուր կողմը կիսենք և քառակուսին բաժանենք չորս մասի: Յուրաքանչյուր մասն իրենից կներկայացնի 1 քառակուսի դյույմ: Նույն գործողությունը կատարենք նաև 3 դյույմ կողմով քառակուսու հետ, այս դեպքում յուրաքանչյուր կողմը բաժանենք երեք հավասար մասի: Արդյունքում կստանանք 9 քառակուսի՝ յուրաքանչյուրը 1 քառակուսի դյույմ մակերեսով:

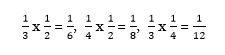
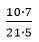
Հետո նույն գործողությունը կատարենք 9 դյույմ երկարությամբ և 6 դյույմ լայնությամբ ուղղանկյան հետ: Բաժանելուց հետո կստանանք 54 հատ 1 քառակուսի դյույմ մակերեսով քառակուսի: Բոլոր այս գործողությունները պատկերված են նկարում: Յուրաքանչյուր դեպքում 1 քառակուսի դյույմ մակերեսով քառակուսիները դասավորված են հորիզոնական տողերում և ուղղահայաց սյունյակներում:

Սյունակում քառակուսիների քանակը համապատասխանում է քառակուսու կամ ուղղանկյան երկարությանը` դյույմերով, իսկ տողում քառակուսիների քանակը՝ քառակուսու կամ ուղղանկյան լայնությանը` դյույմերով: Երկուդյույմանոց քառակուսում երկու սյունակներից յուրաքանչյուրը 2 քառակուսի դյույմ է՝ երկուական մեկ դյույմանոց քառակուսով, 2+2=4: Երեք դյույմանոց քառակուսում երեք սյունակ կա, յուրաքանչյուրում` երեք հատ մեկ դյույմանոց քառակուսի՝ 3+3+3=9:

6×9 դյույմ ուղղանկյան մեջ 6 սյունակներից յուրաքանչյուրը պարունակում է 9 մեկդյույմանոց քառակուսի՝ 9+9+9+9+9+9=54: Կարելի է ուղղանկյունը տողերով հաշվել: 9 տողից յուրաքանչյուրը պարունակում է 6 մեկդյույմանոց քառակուսի` 6+6+6+6+6+6+6+6+6=54:

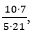
Մակերեսներ

Երկրաչափական պատկերների մակերեսները հաշվելու ընթացակարգի ընդհանուր տեսքը կրկնվող գումարումն է: Քառակուսու և ուղղանկյան դեպքում այդպիսի հաշվարկները շատ պարզ են: Եռանկյունների և շրջանների դեպքում ավելի բարդ է: Անկանոն ձևի մակերեսների դեպքում արդեն բավականին բարդ գործընթաց է: Սակայն մակերեսներ կարողանում էին հաշվել դեռևս հնադարյան գյուղատնտեսական քաղաքակրթության ժամանակ (չենք քննարկի մեր բարձր տեխնոլոգիական քաղաքակրթությունը):
Դեռ վաղ անցյալում չափում էին հողատարածքները և հաշվում մակերեսները, որպեսզի կարողանային տարածքից գանձվող հարկը հաշվել:
(Ես ընդհանրապես կասկածում եմ, որ հին ժամանակներում հարկերը հաշվելու անհրաժեշտությունն էր նպաստում թվաբանության ինտենսիվ զարգացմանը):

Եթե կրկնվող հաշվարկի անհրաժեշտությունը նպաստեց գումարման գործողությունը ստեղծելուն, ապա կրկնվող գումարման անհրաժեշտությունն էլ բերեց թվերի հետ նոր գործողություն ստեղծելուն:

Սկսենք նրանից, որ ընդունենք նոր նշանակում և «վեց անգամ ինը» գրենք այսպես՝ 6×9: «х» նշանն անվանում են բազմապատկման նշան: Այսպիսի գրառումը նշանակում է ինն անգամ վեց կամ վեց անգամ ինն են գումարում: Ինչպես արդեն ցույց տվեցի նախորդ օրինակում (կարող եք ինքնուրույն համոզվել սեփական օրինակը հաշվելով), կարևոր չէ, այս երկու գործողություններից որը կհաշվենք՝ 6х9=9х6:

Այս նոր դիտարկումն օգտագործելով` կարելի է ձևակերպել քառակուսու կամ ուղղանկյան մակերեսը հաշվելու ընդհանուր կանոն: Այս պատկերների մակերեսը հավասար է երկարության և լայնության արտադրյալին: Հաջորդ անհրաժեշտ քայլը բազմապատկման գործողությունը կատարելու պարզ եղանակ գտնելն է: Իհարկե, կարող ենք միշտ օգտվել կրկնվող գումարից, բայց այդ եղանակը անհարմար է և մեծ թվերի դեպքում՝ անարդյունավետ:

Դիցուք, անհրաժեշտ է հաշվել 129 ոտնաչափ և 54 ոտնաչափ ուղղանկյուն տարածքի մակերեսը: Պատասխանը գտնելու համար պետք կլինի 129-ը բազմապատկել 54-ով կամ 54-ը բազմապատկել 129-ով (տվյալ դեպքում` արդեն քառակուսի ոտնաչափով, այլ ոչ թե քառակուսի դյույմով): Սա նշանակում է, որ մեզ անհրաժեշտ է կա´մ հարյուր քսանինը անգամ գումարել հիսունչորս, կա´մ հակառակը՝ հիսունչորս անգամ գումարել հարյուր քսանինը: Ե՛վ մեկը, և՛ մյուսը բավականին ձանձրալի են:

Կամ էլ ուրիշ օրինակ. այս անգամ առևտրային գործարք: Ենթադրենք` անհրաժեշտ է վճարել ինչ-որ առարկաների 254 դյուժինի համար, մեկ դյուժինի համար՝ 72 ցենտ: Այս դեպքում անհրաժեշտ է բազմապատկել 254–ը 72-ով, այսինքն` 72 թիվը 254 անգամ գումարել:
Առօրյա կյանքում ստիպված ենք այսպիսի խնդիրներ անընդհատ լուծել, դրա համար բազմապատկման պարզ և արդյունավետ ձև է անհրաժեշտ:

Մեկից մեկ

Այստեղ նորից հանդիպում ենք ինչ-որ բան անգիր անելու անհրաժեշտությանը: Անհրաժետ է անգիր իմանալ բազմապատկման աղյուսակը, որտեղ ներառված են 1-ից մինչև 9х9 թվերի բոլոր հնարավոր համադրությունները: Դպրոցականները բազմապատկման աղյուսակից կրկնում են արտահայտություններ, օրինակ` 5×2=10, 7х8=56 և այլն, մինչև թվերն իրենք իրենց նրանց ականջին օղ են լինում: Սակայն հենց այդ արգելքը հաղթահարվում է, երեխան հասկանում է, որ արդեն գիտի այն ամենը, ինչն անհրաժեշտ է ցանկացած մեծ թվեր բազմապատկելու համար:

Շատ կարևոր է յուրացնել նաև, որ ցանկացած թիվ զրոյով բազմապատկելիս զրո կստանանք՝ 5×0=0, 155х0=0, 14856734х0=0. Եվ, իհարկե, 0x0=0: Այս պնդումը հեշտ է ստուգել գումարման եղանակով: Եթե գումարում ենք հինգ հատ զրո, ստանում ենք զրո, եթե 155 զրո` նորից զրո ենք ստանում, ինչքան էլ զրո գումարենք, արդյունքում միշտ զրո ենք ստանում:

Սա նշանակում է, եթե մտապահեցիք, որ 7×3=21, ապա հեշտ կլինի բազմապատկել 70-ը 3-ով կամ 7-ը 30-ով: 70х3=210, 7х30=210. Բազմապատկման գործողությունները զրոյի վրա չեն ազդում. եթե կատարում եք 70х30 բազմապատկումը, ապա երկու զրոներն էլ պահպանվում են 70х30=2100:

Առաջ գնանք: Անհրաժեշտ է զրոյից տարբեր թվանշաններից կազմված թվեր բազմապատկել: Դրա համար թվերը ներկայացնենք կարգային գումարելիների տեսքով, ինչպես արդեն արել ենք գումարման դեպքում: Օրինակ, անհրաժեշտ է 3965 х 7 արտադրյալը գտնել: (Արտադրյալը թվերի բազմապատկման արդյունքն է, ինչպես գումարը՝ գումարման): 

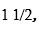
3965 թիվը կարելի է ներկայացնել որպես 3000+900+60+5: Այժմ հեշտ է բազմապատկում կատարելը, քանի որ թվերից յուրաքանչյուրը կազմված է միայն մեկ իմաստալից թվանշանից, իսկ մնացածը զրոներ են:

Կարևոր չէ, թե ինչ հերթականությամբ կկատարենք բազմապատկումը: Կարելի է աջից ձախ անել, ձախից աջ կամ խառը: Ես կատարում եմ այնպես, ինչպես ինձ դպրոցում են սովորեցրել, այսինքն` աջից ձախ: Բացի դրանից, դպրոցում մեզ սովորեցնում են թվերը կարգային գումարելիների չբաժանել և անտեսել զրոները: Այս դեպքում նախորդ օրինակի գրառումը ավելի պարզ կլինի.

Սովորեցնելու ժամանակ այդպիսի գրառման առավելություններն ակնհայտ են. սովորողն արագ ու հեշտ յուրացնում է բազմապատկումը և կարողանում է մեծ թվերն արագ բազմապատկել: Ուսուցման ժամանակ գրառման տվյալ ձևի թերությունն այն է, որ սովորողը բազմապատկման գործողությունը կատարում է զուտ մեխանիկորեն և հաճախ չի պատկերացնում` ինչու է այդպես արել: Բացի այդ կրճատ գրառման ձևից, թվերը մտովի բազմապատկել ենք սովորում: Բայց դրանք բազմապատկման տեխնիկայի հարցեր են, սկզբունքը մնում է անփոփոխ:

Երբ պետք է տասից մեծ երկու թիվ բազմապատկել, լրացուցիչ բարդություններ են առաջանում: Այս դեպքում երկու թիվն էլ ներկայացնում ենք կարգային գումարելիների գումարի տեսքով և բազմապատկում ենք տվյալ թվի մասերը մյուս թվի մասերով:

Այսպիսով, եթե անհրաժեշտ է բազմապատկել 35 և 28, կատարում ենք հետևյալ սխեմայով (նկարի սլաքները ցույց են տալիս բազմապատկման հերթականությունը, երևի այսպիսի սխեմայից է առաջացել բազմապատկման «х» նշանը):

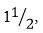
Մեծ թվեր բազմապատկելու ժամանակ էլ ենք նույն մեթոդիկան օգտագործում. նույնիսկ բազմապատկման պարզեցված սխեման, որը մեզ դպրոցում սովորեցնում են, մեծ ուշադրություն է պահանջում, այլապես կարող ենք հաշվարկներում խճճվել: Կարող եք համոզվել ներքևում բերված օրինակով.

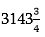
Իհարկե այս մեթոդն էլ հեշտ չէ, բայց ավելի գործնական է, քան բազմակի գումարելով հաշվելը: Պատկերացրեք, վերջին դեպքում պետք է գումարեինք` 3965+3965+3965+3965+3965+… և այդպես` 2197 անգամ:

Բազմապատկման հակառակը

Գումարման հակառակ գործողությունը հանումն է, բազմապատկումն էլ հակառակ գործողություն ունի, որի անունը բաժանում է: Եթե բազմապատկումը բազմակի հաջորդական գումարումն է, ապա բաժանումը՝ բազմակի հաջորդական հանումն է: Դիցուք, ցանկանում եք 15-ը բաժանել 3-ի, այս գործողությունը գրառում են այսպես 15:3, որտեղ «:»-ը բաժանում է նշանակում: Այս գործողությունը կատարելու եղանակներից մեկը 15-ից հաջորդաբար 3 հանելն է: Այսպես, 15-3=12, 12-3=9, 9-3=6, 6-3=3, 3-3=0. Զրոյի հասանք հանման հինգ գործողությամբ, այսինքն` 15:3=5:

Բայց, իհարկե, ոչ ոք երբեք այդպես չի անում: Դրա փոխարեն օգտագործում են նույն մեթոդիկան, ինչ բազմապատկման դեպքում: Եթե բաժանենք 15-ը 3-ի, կստանանք մի թիվ, որը բազմապատկելով 3-ով նորից 15 կստանանք: Մենք գնացինք առաջ, վերադարձանք և հայտնվեցինք նույն տեղում: (Դրան արդեն առնչվել էինք գումարման և հանման ժամանակ, որոնք նույնպես հակառակ գործողություններ են: Եթե 7-4=3, ապա 3+4=7):

Այսպիսով, մեր խնդիրը կարելի է այսպես ձևակերպել: Ի՞նչ թվով կարելի է բազմապատկել 3-ը, որպեսզի 15 ստանանք: Չեմ կասկածում, որ անգիր գիտեք բազմապատկման աղյուսակը, որը ցածր դասարաններում մտցնում են դպրոցականների գլուխները. դրա համար էլ մեխանիկորեն հիշում եք, որ 15 ստանալու համար պետք է 3-ը բազմապատկել 5-ով:

Քանի որ 5х3=15, ապա 15:3=5, և 15:5=3: Բազմապատկման աղյուսակի միևնույն տողը բաժանման երկու գործողության պատասխան է տալիս: Ուշադրություն դարձրեք, բաժանման ժամանակ, ինչպես հանման դեպքում, արտահայտության մեջ անդամների դասավորությունը նշանակություն ունի: 5×3-ը հավասար է 3х5, բայց 15:5-ը հավասար չէ 5:15: Բաժանման նշանից ձախ գրառված թիվը բաժանելի են անվանում, բաժանման նշանից աջ՝ բաժանարար, գործողության արդյունքը՝քանորդ: Այսպիսով, 15:5=3 արտահայտության մեջ 15-ը բաժանելին է, 5–ը` բաժանարարը, իսկ 3–ը` քանորդը:

Որ բաժանումը հակառակ գործողություն է, այսինքն` ավելի բարդ թվաբանական գործողություն է, գիտի յուրաքանչյուր դպրոցական:

Դիցուք, պետք է 7715-ը բաժանել 5-ի: Պատկերացնո՞ւմ եք, թե քանի անգամ պետք է 7715-ից 5 հանենք, որպեսզի 0-ին հասնենք և պատասխանը ստանանք: Բազմապատկման աղյուսակն այս հարցի պատասխանը չի տալիս: Բա ի՞նչ անենք:

Այս դեպքում նորից կօգնի 0-ով բազմապատկելը: Գիտեք, որ 1×5=5, հետևաբար, 1000х5=5000. Այս թիվն արդեն բավականաչափ մոտ է 7715-ին, բայց պակասում է 2715: Այս թիվը բաժանենք 5-ի: Բազմապատկման աղյուսակից գիտեք, որ 5х5=25, կնշանակի՝ 500х5=2500, կմնա ընդամենը 215-ը: Առաջ գնանք: Քանի որ 4 х 5 = 20, հետևաբար, 40 х 5 = 200. Մնում է միայն 15-ը: Այս թիվը հեշտ է բաժանվում 5-ի, գիտենք, որ պատասխանը 3-ն է:

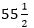Սկզբում 5-ը բազմապատկեցինք 1000-ով, հետո 500-ով, հետո 40-ով և, վերջապես, 3-ով: Գումարենք բոլոր արդյունքները և կստանանք 1543. Քանի որ 1543 х 5 = 7715, հետևաբար, 7715:5=1543, հենց դա էլ պատասխանն է, այսինքն` քանորդը:

10-ից մեծ թվերի վրա բաժանելն ավելի բարդ է, քանի որ բազմապատկման աղյուսակի ամենամեծ արտադրիչը 10-ն է: Բայց սկզբունքը նույնն է, չնայած ստիպված ենք սկզբում պատասխանը «գուշակել», հետո ստուգել, թե ինչքանով է այն ճիշտ:

(Այնուամենայնիվ, մեր դպրոցականները հանդիպում են ավելի պարզ խնդրի, քան անցյալի մաթեմատիկոսները, քանի որ մեզ մոտ արաբական թվանշաներ են: Այն ժամանակներում, երբ դեռ արաբական թվանշանները չէին գործածվում, մեծ թվերի բաժանումը կամ «երկար բաժանումը» իսկական արվեստ էր՝ միայն վարպետ մաթեմատիկոսներին հասու):

Նշանների դիրքը

Այս գլխի սկզբում արդեն պատմել եմ, թե ինչպես են գումարվում և հանվում բացասական թվերը: Այժմ եկեք դիտարկենք բազմապատկումը և բաժանումը:

Դիցուք, պետք է +3-ը բազմապատկել -4-ով: Ինչպե՞ս անենք:

Եկեք այսպիսի իրավիճակ դիտարկեք: Երեք մարդ պարտքի տակ ընկավ, և յուրաքանչյուրը 4 դոլար պարտք ուներ: Ինչքա՞ն է ընդհանուր պարտքը: Հաշվելու համար պետք է երեք պարտքն իրար գումարենք: 4դոլար+4դոլար+4դոլար=12դոլար: Արդեն հասկացել ենք, որ երեք հատ չորս գումարելը նշանակվում է 3×4:Քանի որ խոսում ենք պարտքի մասին, 4-ից առաջ դրվում է «-» նշանը: Գիտենք, որ ամբողջ պարտքը 12 դոլար է, այնպես որ խնդիրն այս տեսքն ունի՝ 3х(-4)=-12.

Նույն արդյունքը կստանայինք, եթե խնդրի պայմանի համաձայն չորս մարդ ունենար 3-ական դոլար պարտք: Այլ կերպ ասած` (+4)х(-3)=-12. Բայց քանի որ արտադրիչների հերթականությունը նշանակություն չունի, կստանանք (-4)х(+3)=-12, և (+4)х(-3)=-12.

Եկեք արդյունքներն ընդհանրացնենք: Մեկ բացասական և մեկ դրական թիվ բազմապատկելիս արդյունքը միշտ բացասական թիվ կլինի: Պատասխանի թվային արժեքը նույնը կլինի, ինչպես դրական թվերի դեպքում, (+4)х(+3)=+12 արտադրյալը: «-» նշանի առկայությունն ազդում է ոչ թե թվային արժեքի, այլ միայն նշանի վրա:

Իսկ ինչպե՞ս բազմապատկենք երկու բացասական թվեր:

Ցավոք, դժվար է կյանքից հարմար օրինակ բերել այս թեմայով: Հեշտ է պատկերացնել 3 կամ 4 դոլարի պարտք, բայց անհնար է պատկերացնել պարտքի տակ ընկած -4 կամ -3 մարդու: Թերևս այլ ճանապարհով գնանք: Բազմապատկման դեպքում արտադրիչներից մեկի նշանը փոխելիս փոխվում է արտադրյալի նշանը: Եթե փոխում ենք երկու արտադրիչների նշանները, պետք է երկու անգամ փոխենք արտադրյալի նշանը, սկզբում դրականից բացասական, հետո հակառակը՝ բացասականից դրական, այսինքն` արտադրյալը իր սկզբնական նշանը կունենա:

Ուստի, լրիվ տրամաբական է, չնայած մի փոքր տարօրինակ, որ (-3)х(-4)=+12:

Բազմապատկման ժամանակ նշանի դիրքը փոխվում է հետյալ կերպ.

դրական թիվхդրական թիվ = դրական թիվ.
բացասական թիվ х դրական թիվ = բացասական թիվ.
դրական թիվ х բացասական թիվ = բացասական թիվ.
բացասական թիվ х բացասական թիվ = դրական թիվ:

Այլ կերպ ասած, երկու նույն նշաններով թվեր բազմապատկելիս դրական թիվ է ստացվում: Երկու տարբեր նշաններով թվեր բազմապատկելիս բացասական թիվ է ստացվում: Նման կանոնը ճիշտ է նաև բազմապատկման հակառակ գործողության՝ բաժանման համար:

(+12):(+3)=+4;
(+12):(-3)=-4;
(-12):(+3)=-4;
(-12):(-3)=+4.

Հեշտությամբ կարող եք դրանում համոզվել` բազմապատկման հակառակ գործողություն կատարելով: Եթե վերևում բերված օրինակներից յուրաքանչյուրում քանորդը բաժանարարով բազմապատկեք, բաժանելին կստանաք, և կհամոզվեք, որ այն նույն նշանն ունի, օրինակ՝ (-3)х(-4)=(+12):

Բաժանե՞լ, թե չբաժանե՞լ

Քանի որ մենք սահմանեցինք բաժանումը որպես հաջորդական բազմակի հանում, որի արդյունքում զրո ենք ստանում, պարզվում է, որ դա ոչ միշտ է հնարավոր: Փորձենք 7-ը 2-ի բաժանել:

Հաջորդական հանման արդյունքում կստանանք 7-2-2-2=1, և այստեղ ստիպված ենք կանգ առնել: Եթե ևս մեկ հատ երկու հանենք, կհայտնվենք բացասական թվերի տարածքում: Նույնիսկ եթե ընդունում ենք բացասական թվերի գոյությունը, իսկ հին ժամանակներում դրա մասին չգիտեին, չենք կարող հանում կատարել բացասական թվերի տիրույթում:

Ենթադրենք, որ ևս մի քանի քայլ ենք կատարում. 1-2=-1, հաջորդ քայլը՝ -1- 2=-3, հետո՝ -3-2=-5, և այդպես մինչ անվերջություն: Որտե՞ղ պիտի կանգ առնենք: Կարծես թե մեր համակարգը խափանվեց:

Փորձենք ուրիշ ճանապարհով գնալ: Հիշենք բազմապատկման աղյուսակը: Իհարկե, այնտեղ չենք գտնի թիվ, որը 2-ով բազմապատկելիս 7 ստանանք, բայց 2х3=6, իսկ 2х4=8.

Հետևաբար, եթե բաժանումը սահմանում ենք որպես հաջորդական հանում, ինչ-որ դեպքում բաժանումը հնարավոր է, իսկ ինչ-որ դեպքում՝ոչ:

Հին հույներին թվերի այս հատկությունը զարմացնում էր, և նրանք դրան յուրօրինակ մեկնաբանություն տվեցին:
Ո՞ր թվերն են բաժանվում 2-ի, իսկ որո´նք չեն բաժանվում: 1-ը չի բաժանվում, 2-ը բաժանվում է, 3-ը չի բաժանվում, 4-ը բաժանվում է, 5 -ը չի բաժանվում, 6 -ը բաժանվում է…

Դեռ հին ժամանակներում թվերը բաժանել են երկու խմբի՝ որ բաժանվում են 2-ի, և որ չեն բաժանվում 2-ի: Հին Հունաստանի մաթեմատիկոսները համարում էին, որ թվերը առեղծվածային իմաստով են օժտված: Նրանց պատկերացմամբ, այն թվերը, որոնք բաժանվում էին 2-ի, կանացի սկիզբ ունեին և դժբախտ էին: Այն թվերը, որոնք 2-ի չէին բաժանվում, հույների կարծիքով, արական էին և երջանիկ: (Հաշվի առեք, որ հույն մաթեմատիկոսները բացառապես տղամարդ էին և իհարկե, երջանկություն էին վերագրում իրենց):

Առօրյա կյանքում թվի բաժանելիությունը 2-ի մեծ նշանակություն ուներ, քանի որ հաճախ էր հարկ լինում որոշակի քանակով առարկաներ բաժանել երկու մարդու միջև: Արդարացի բաժանելը վեճից խուսափելու լավագույն միջոցն է: Հին ժամանակներում, երբ մարդիկ վատ էին գլուխ հանում թվաբանությունից, արդարացի բաժանելու ամենապարզ տարբերակը առարկաները երկու կույտի բաժանելն էր, այնպես, որ մի կույտի յուրաքանչյուր առարկային մյուսից իր զույգը համապատասխանի: Պատկերացնենք, այդ առարկաները ֆիշկաների տեսքով, որոնք կարելի է սյուներով դասավորել (ինչպես նկարում է պատկերված): Եթե առարկաների ընդհանուր թիվը բաժանվում է 2-ի, կստանանք երկու սյուն` յուրաքանչյուրում հավասար քանակությամբ ֆիշկա: Եթե սկզբում 16 ֆիշկա ունենայինք, կստանայինք նույն բարձրության երկու սյուն՝ 8-ական ֆիշկայով, քանի որ 16 թիվը բաժանվում է 2, այսինքն զույգ թիվ է:

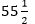
Եթե սկզբում 17 ֆիշկա ունենայինք, կստանայինք անհավասար բարձրություններով երկու սյուն, մեկում` 8 ֆիշկա, մյուսում՝ մեկով ավելի, քանի որ 17 թիվը 2-ի չի բաժանվում, այսինքն` կենտ թիվ է: Մյուս թվերի վրա բաժանվելը և չբաժանվելը որոշակի կախվածություններ են ենթադրում, բայց ավելի բարդ, քան զույգ-կենտ բաժանումը:

Հույները զվարճանում են

Բաժանման բնագավառում ևս մեկ հայտնագործություն էր արվել. որոշ թվեր բաժանվում են մեկից ավելի ամբողջ թվերի: Օրինակ, 60-ը բաժանվում է 2, 3, 4, 5, 6, 10, 12, 15, 20 և 30 թվերի: Այս բոլոր թվերը կոչվում են 60-ի բաժանարարներ: Հետևաբար, 60-ը տասը տարբեր բաժանարար ունի:

Դրանցից բացի, ևս երկու բաժանարար կա, որոնց մասին ավելի վաղ եմ խոսել: Դա 1-ն է, և ինքը՝ 60-ը: Վերջապես, 60:60=1, քանի որ յուրաքանչյուր թիվ ինքն իրեն բաժանելիս մեկ ենք ստանում: Մյուս արտադրիչը 1-ն է: Իրոք, 60:1=60: Ցանկացած թիվ մեկի բաժանելիս անփոփոխ է մնում, այսինքն` 1-ը համապիտանի բաժանարար է:

Քանի որ յուրաքանչյուր թիվ առանց մնացորդի բաժանվում է մեկի և իր վրա, հույները, որոնք հաճույքով լուծում էին բաժանարարների հետ կապված ամենատարբեր գլուխկոտրուկներ, ուղղակի անտեսում էին այդ երկու բաժանարարները: Դրանք ի՞նչ հետաքրքրություն կարող են ներկայացնել, եթե այդպիսի բաժանարար բոլոր թվերն ունեն: (Բացի դրանից, այժմ կարող ենք ասել, որ յուրաքանչյուր թիվ բացասական բաժանարար ունի: Օրինակ, 60 թվի համար դրանք -2, -3, -4, -5, -6, -10, -12, -15, -20 և -30 թվերն են: Բայց հույներին բացասական թվերը հայտնի չէին, բացի դրանից, բացասական բաժանարարները փաստորեն մեզ ոչ մի նոր ինֆորմացիա չեն տալիս, դրա համար էլ այդ բաժանարարները նույնպես չենք դիտարկի:)

Եթե 60 թիվը 10 բազմապատիկ ունի, թվային առանցքի նրա հարևանների բախտը այնքան էլ չի բերել: Օրինակ, 58 թիվը միայն 2 բաժանարար ունի՝ 2-ը և 29-ը, 62 թիվը՝ 2 և 31. Անկախ նրանից, թե քանի բաժանարար ունի թիվը, եթե այդպիսի բաժանարարներ կան, այդպիսի թիվը կոչվում է բաղադրյալ, քանի որ այն կարելի է կազմել ուրիշ, ավելի փոքր թվեր բազմապատկելով: Այսպես, 58 թիվը 2х29 է, իսկ 62 թիվը` 2х31.

60 թվի դեպքը ավելի բարդ է, քանի որ այն մի քանի բաժանարար ունի: Այն կարելի է ներկայացնել 2х30 տեսքով, բայց 30 թիվն էլ է բաղադրյալ, այն կարելի է ներկայացնել 2х15 տեսքով, այնինչ 15-ը նույնպես բաղադրյալ է և հավասար է 3×5: Այսպիսով կստանանք՝ 60=2x2x3x5:

2, 3 և 5 թվերը արտադրիչների վերլուծելու ոչ մի փորձ չենք արել: Դա հնարավոր էլ չէ: 29-ը ու 31-ը այդպիսի թվեր են, որ բացի մեկից և իրենից, ուրիշ արտադրիչ չունեն: Այլ կերպ ասված, համոզվեցինք, որ կան այնպիսի թվեր, որոնք առանց մնացորդի հնարավոր չէ բաժանել ուրիշ արտադրիչի, բացի մեկից և իրենից:

Այն թվերը, որոնք հնարավոր չէ տրոհել արտադրիչների, կոչվում են պարզ թվեր, ի տարբերություն բաղադրյալ թվերի, որոնք հնարավոր է արտադրիչների տրոհել:

Մարդիկ հաճախ թվերի մեջ ինչ-որ առեղծվածային իմաստ են տեսնում, և այդ տեսանկյունից կարող է թվալ, որ հենց պարզ թվերն են առաջինը հայտնվել, ի վերջո ցանկացած բաղադրյալ թիվ պարզ թվերի արտադրյալից է ստացվում: Ասենք, այն բանից հետո, երբ հայտնվեցին 2, 3 և 5 թվերը, կարելի է ստանալ 60 թիվը, հավասար՝ 2х2х3х5:

Կարող է թվալ, եթե թվային առանցքով վեր բարձրանանք, ապա հաջորդ պարզ թիվը գտնելու հնարավորությունը կփոքրանա, և վերջիվերջո ինչ-որ պարզ թիվ կլինի ամենամեծ պարզ թիվը: Բայց դա իրականությանը չի համապատասխանում: Դեռ 2200 տարի առաջ հույն մաթեմատիկոս Էվկալիդեսը ապացուցեց, որ գոյություն չունի այնքան մեծ պարզ թիվ, որից ավելի մեծը հնարավոր չլինի գտնել: Այսինքն` «ամենամեծ պարզ թիվ» սկզբունքորեն գոյություն չունի:

Ինչպես արդեն ասել եմ, հույները սիրում էին թվային տարբեր գլուխկոտրուկներ գուշակել և օրինաչափություններ փնտրել: Օրինակ, հաշվում էին տարբեր թվերի բաժանարարների գումարը, այս դեպքում ներառելով նաև 1-ը, և տեսնում, թե ինչ է ստացվում: Նրանք պարզեցին, որ բաժանարարների գումարը կարող է այդ թվից փոքր կամ մեծ լինել կամ հավասար լինել: Օրինակ 10 թվի բաժանարարների (1, 2 и 5) գումարը հավասար է 8-ի: 10 թիվն անվանում են թերի թիվ: 12 թվի բաժանարարների (1, 2, 3, 4 և 6)  գումարը 16 է, այսինքն` մեծ է իրենից: Այնպիսի թվերը, ինչպեսին 12-ն է, անվանում են ավելցուկային:

6 թվի բաժանարարների գումարը (1, 2 և 3) հավասար է հենց իրեն, նույնը վերաբերում է նաև 28 թվին (1, 2, 4, և 7): Այդպիսի թվերը հույներն անվանեցին կատարյալ: Եվս մեկ հետաքրքիր օրինաչափություն կա: 220 թվի բաժանարարների (1, 2, 4, 5, 10, 11, 20, 22, 44, 55 և 110) գումարը 284 է, և, միևնույն ժամանակ, 284-ի (1, 2, 4, 71, 142) բաժանարարների գումարը 220 է: Այդպիսի թվերը հույներն անվանեցին բարեկամ թվեր:

Թվերի բաժանումը` պարզ, բաղադրյալ, բարեկամ և այլ թվերի, գործնական մեծ արժեք չունի, բայց հազարամյակներ շարունակ թվային օրինաչափությունները մաթեմատիկոսների հիացմունքն ու հետաքրքրությունն են առաջացրել: Հետաքրքրությունը նրանց հանդեպ չի մարել և մեր օրերում:

Հաշվում ենք և չափում

Մինչ այժմ գործ ունեինք սովորական թվերի հետ, որոնց շնորհիվ կարող ենք տարբեր առարկաներ հաշվել` 1, 2, 3… Շատ հաճախ ուրիշ թվեր չեն էլ պահանջվում:

Օրինակ,այդպիսի թվով կարելի է որոշել դասասենյակում տղաների քանակը: Սենյակում կարող է լինել 4 տղա, 5 տղա կամ այլ քանակի տղաներ: Ամեն դեպքում դա լրիվ որոշակի թիվ է: Բայց դուք ոչ մի կերպ չեք կարող հայտարարել. «Ես, ուշադիր հաշվեցի և պարզեցի, որ սենյակում 4-ից ավելի, բայց 5-ից պակաս տղա կա: Կարծում եմ, ինչ-որ միջանկյալ թիվ է 4-ի և 5-ի միջև»:

Եթե դուք ինչ-որ առարկաներ եք հաշվում, 4-ի և 5-ի միջև ոչ մի ուրիշ թիվ չկա: Սենյակում կա´մ 4, կա´մ 5 տղա կա, և միջանկյալ ոչ մի թիվ: Եթե սենյակը, որտեղ արդեն 5 տղա կա, մտնի մեկը, սենյակում կլինի 6 տղա, ընդ որում ճիշտ 6, ոչ թե մոտ 6 կամ 6-ից մի քիչ շատ: Սակայն եթե դուք հետաքրքրվում եք, թե տղաները որքան ժամանակ տրամադրեցին պարապմունքներին, կարող եք մոտավոր պատասխան ստանալ. «Նրանք պարապեցին մեկ ժամից ավելի, վստահ չեմ, բայց, իմ կարծիքով, երկու ժամից քիչ»:

Այս դեպքում պատասխանն անիմաստ չէ, քանի որ գոյություն ունի մեկ ժամից մեծ, բայց երկու ժամից փոքր ժամանակահատված: Ժամանակը չափում են, ոչ թե հաշվում:

Հաշվելը և չափելը տարբեր գործընթացներ են: Հաշվարկելիս գործ ունեք առանձին կամ դիսկրետ օբյեկտների հետ: Այն թվերը, որոնք սովորեցինք գրքի սկզբում, նույնպես առանձին կամ դիսկրետ թվեր են, և նրանք լավ համապատասխանում են դիսկրետ օբյեկտներին: Դիսկրետ օբյեկտներ ուսումնասիրելիս մեզ ուրիշ թվեր պետք չեն: Եթե ստիպված ենք ինչ-որ բան չափել, որը առանձին օբյեկտներից չի կազմված, խնդիրը անմիջապես բարդանում է: Այժմ գործ ունենք ձգվածության կամ անընդհատության հետ, այսինքն` ինչ-որ գործընթացի ժամանակի տևողության կամ ինչ-որ գծի երկարության հետ:

Սովորական դիսկրետ թվերը չեն համապատասխանում ձգված մեծություններին, և նրանց չի կարելի օգտագործել այդպիսի մեծություններ չափելու համար՝ առանց վտանգելու ճշտությունը:

Որպեսզի խուսափենք այդպիսի անհամապատասխանությունից, անհրաժեշտ է դիսկրետ թվերի շարքում տեղադրել ինչ-որ միջանկյալ թվեր: Երբ դա կանենք, 1, 2, 3, 4…թվերը կդառնան միայն մի փոքր մասը անսահման համակարգի, որը կհամապատասխանի այնպիսի հասկացությունների, ինչպես ժամանակը, երկարությունը կամ ցանկացած ուրիշ անընդհատություն:

Հաջորդ գլխից կսկսենք ուսումնասիրել այդպիսի թվեր, կպարզենք դրանց ծագումը և կսովորենք այդ թվերի օգնությամբ հաշվարկելու կանոնները:

Շարունակությունը

Թարգմանություն ռուսերենից

Խմբագիր՝ Գևորգ Հակոբյան