Հեղինակ՝ Դմիտրի Եֆիմով
Նայելով «Քվանտ» ամսագրի արխիվը՝ համարներից մեկում հեղինակը գտավ Ի․ Ֆ․ Ակուլիչի հետևյալ խնդիրը․ «Ճանապարհային» շախմատի տախտակը խաղադաշտի սահմաններին ունի փոքրիկ եզրեր, որոնք խաղաքարերին թույլ չեն տալիս թափվել։
Ինչպես նաև առկա է 28 խաղաքարից բաղկացած դոմինոյի ամբողջական հավաքածու, որի խաղաքարերից յուրաքանչյուրը ծածկում է խաղադաշտի ճիշտ երկու հարևան վանդակ։
Հնարավոր է արդյո՞ք դոմինոյի հավաքածուն այնպես շարել շախմատի տախտակին, որ դոմինոյի ոչ մի խաղաքար հնարավոր չլինի տեղաշարժել տախտակի հարթությունում։
Եթե հաշվի առնենք, որ տախտակի վրա դոմինոյի խաղաքարերի անշարժ լինելու պայմանը համարժեք է նրան, որ ոչ մի խաղաքար իր կարճ կողմով չհպվի դատարկ վանդակի և իր երկար կողմով չհպվի երկու հարևան դատարկ վանդակների, ապա մի քիչ մտածելով՝ հարցին կարելի է տալ դրական պատասխան, տես օրինակը պատկերված նկար 1-ում։
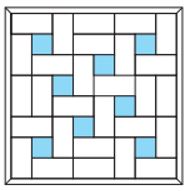
Նկար 1․ «Ճանապարհային» շախմատի տախտակի և դոմինոյի խնդիրների լուծում
Այստեղ դոմինոյի խաղաքարերով չծածկված վանդակները ներկված են կապույտ։
Բնական հարց է առաջանում՝ կարո՞ղ ենք լավացնել այս արդյունքը, այսինքն՝ կարելի՞ է արդյոք օգտագործել դոմինոյի ավելի քիչ խաղաքար։
Իսի ինչպիսի՞ն կլինի արդյունքը այլ չափսերով խաղատախտակի համար։
Այս հոդվածում մենք կաշխատենք պատասխանել այս հարցերին։
Կոշտ դասավորություններ և դրանց հատկությունները
Ներմուծենք մի քանի ընդհանուր սահմանում։ Դիտարկենք nxn չափսերով քառակուսաձև տախտակ։
Ենթադրենք՝ դոմինոյի խաղաքարերը առանց վերադրվելու տեղադրված են տախտակի վրա այնպես, որ յուրաքանչյուր խաղաքար ծածկում է ճիշտ երկու հարևան վանդակ։
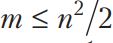
Այսպիսի դասավորությունը անվանենք շարվածք։ Ընդ որում, տախտակի որոշ վանդակներ կարող են ծածկված չլինել։ Այդպիսի վանդակներն անվանենք անցքեր։
Կասենք, որ դոմինոյի շարվածքը կոշտ է, եթե խաղաքարերից ոչ մեկն իր կարճ կողմով չի հպվում դատարկ անցքի և երկար կողմով չի հպվում երկու հարևան անցքի ( նկար 2)

Նկար 2․Դոմինոյի խաղաքարի և անցքերի փոխադարձ դասավորության անհնար դիրքեր կոշտ շարվածքի դեպքում
Միանգամայն ակնհայտ է, որ եթե n=3, ապա շարվածքը կլինի կոշտ այն ժամանակ և միայն այն դեպքում, եթե յուրաքանչյուր դատարկ վանդակ շրջափակված լինի խաղաքարերով այնպես, ինչպես ցույց է տրված նկար 3-ում, տես նկարը։
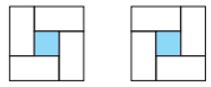
Նկար 3. Կոշտ շարվածքի անհրաժեշտ և բավարար պայմաններ
Կոշտ շարվածքը կանվանենք նվազագույն, եթե այն տրված չափսերով տախտակի համար պարունակում է դոմինոյի հնարավոր ամենաքիչ խաղաքար։ Պարզ է, որ կոշտ շարվածքը կհանդիսանա նվազագույն այն ժամանակ և միայն այն դեպքում, երբ այն տրված չափսերով տախտակի համար պարունակի հնարավոր առավելագույն քանակով անցքեր։ Մեզ կհետաքրքրի նվազագույն կոշտ շարվածքի կառուցումը քառակուսաձև տախտակի տարբեր չափսերի դեպքում։
Հաշվի առնելով վերևում ասվածը՝ կարող ենք տրված խնդիրը վերաձևակերպել ծածկելու և փաթեթավորելու խնդիրների ոգով։
nxn չափսերով տախտակի վրա տեղավորենք որքան հնարավոր է շատ 3×3 չափսերով պատկերներ, որոնք կազմված են դոմինոյի չորս հատ 2×1 չափսերով խաղաքարերից և 1×1 չափսերով անցքից, տես նկար 3-ը, այս դեպքում թույլատրվում է երկու խաղաքարերի հատումը դոմինոյի մեկ խաղաքարով, իսկ տախտակի բոլոր այն վանդակները, որոնք ծածկված չեն այդ խաղաքարերով, պետք է ամբողջությամբ ծածկվեն դոմինոյի խաղաքարերով։ Տախտակի այն մասը, որը կազմված է բոլոր վանդակներից՝ բացառությամբ եզրի երկայնքով տեղադրված վանդակներից, անվանենք տախտակի միջուկ: Պարզ է, որ 2×2 չափսերով տախտակը միջուկ չունի, իսկ 3×3 չափսերով տախտակի միջուկը մեկ կենտրոնական վանդակն է։ Վերը ասվածից հետևում է, որ կոշտ դասավորության դեպքում անցքերը կարող են գտնվել միայն տախտակի միջուկում։
Դժվար չէ նկատել, որ նկար 4-ում պատկերված երկու անցքերի փոխադարձ դասավորությունները, 90 աստիճան պտույտի ճշտությամբ, հնարավոր չեն կոշտ շարվածքի դեպքում։
Այստեղից էլ հետևում է, որ կոշտ շարվածքի դեպքում տախտակի 2×2 չափսերով ցանկացած քառակուսի մաս պարունակում է մեկից ոչ ավելի անցք, իսկ տախտակի 3×3 չափսերով ցանկացած քառակուսի մաս՝ երկուսից ոչ ավելի։
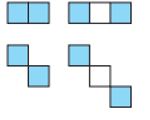
Նկար 4․ Երկու անցքերի փոխադարձ դասավորությունները, որ հնարավոր չեն կոշտ դասավորության դեպքում
Առաջադրանք 1. Ցույց տվեք հինգ վանդակից (պարտադիր չէ կողմով կից լինեն) կազմված պատկերներ, որ կոշտ շարվածքի դեպքում տախտակի նման պատկերներ ներկայացնող ցանկացած տիրույթ պարունակի մեկից ոչ ավելի անցք։
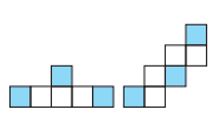
Նկար 5․Երեք դատարկ վանդակների փոխադարձ դասավորությունը կոշտ դասավորության դեպքում անհնար է
Կոշտ դասավորության դեպքում նաև գոյություն ունեն մի քանի սահմանափակումներ երեք անցքերի փոխադարձ դասավորության համար, եթե անգամ անցքերի զույգերի դասավորությունը թույլատրելի է։
Երկու այդպիսի անհնար դասավորության օրինակ պատկերված է նկար 5-ում․ պտույտի ճշգրտությամբ՝
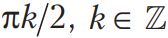
Եթե դոմինոյի խաղաքարերի շարվածքի դեպքում ստացվել է այդպիսի դատարկ վանդակներ, ապա ծայրահեղ դեպքում մի խաղաքարը կարճ կողմով կից կլինի անցքին։
Հաշվի առնելով այս փաստը՝ ոչ շատ վերադասավորումներից հետո կարելի է ցույց տալ, որ կոշտ դասավորության դեպքում՝ տախտակի 2×5 կամ 5×2 ուղղանկյան տեսքով ցանկացած տիրույթ պարունակում է երկուսից ոչ ավելի անցք, իսկ 3×5 կամ 5×3 ուղղանկյան տեսքով ցանկացած տիրույթ՝ ոչ ավելի քան երեք անցք։
Առաջադրանք 2. Ցույց տվեք 11 և 12 վանդակներից կազմված այնպիսի պատկերներ, որ կոշտ դասավորության դեպքում տախտակի ցանկացած տիրույթ, որը ներկայանում է այդ պատկերների տեսքով պարունակի ոչ ավելի քան երկու անցք։
Այս բաժինը եզրափակենք բավականին ակնհայտ, բայց օգտակար պնդումով։
Պնդում 1. Կոշտ դասավորության դեպքում nxn չափսերով տախտակի դատարկ վանդակների զույգությունը համընկնում է n թվի զույգության հետ։
Փոքր չափսերով տախտակի կոշտ շարվածքներ
Սկսենք տախտակի նվազագույն չափից, որի վրա կարելի է տեղադրել դոմինոյի գոնե մեկ խաղաքար, այսինքն՝ 2 x 2 չափսերով տախտակից: Ակնհայտ է, որ այդպիսի տախտակը թույլ է տալիս ընդամենը երկու կոշտ շարվածք՝ դոմինոյի երկու կից քարեր՝ տեղադրված ուղղաձիգ կամ հորիզոնական: 3×3 չափսերով տախտակը նույնպես թույլ է տալիս ընդամենը երկու կոշտ շարվածք։ Դրանք ներկայացված են նկար 3-ում։
Oգտագործելով պնդում 1-ը՝ կարելի է հեշտությամբ ապացուցել, որ 4×4 չափսերով տախտակը ցանկացած կոշտ շարվածքի դեպքում անցքեր չի պարունակում։
Իրոք, այդ չափսերով տախտակի միջուկը 2×2 չափսերով քառակուսի է։
Ամենափոքր դրական զույգ թիվը 2-ն է, բայց ինչպես գիտենք 2×2 չափսերով տախտակը կոշտ շարվածքի դեպքում չի կարող ունենալ մեկից ավելի անցք։։
Նման ձևով կարելի է ցույց տալ, որ 5×5 չափսերով տախտակը ցանկացած կոշտ շարվածքի դեպքում պարունակում է ճիշտ մեկ անցք։ Իրոք, այդ չափսերով տախտակի միջուկը 3×3 չափսերով քառակուսի է, որը ինչպես գիտենք, կոշտ շարվածքի դեպքում կարող է պարունակել երկուսից ոչ ավելի անցք։
Հաշվի առնելով պնդում 1-ը՝ կոշտ շարվածքի դեպքում 5×5 չափսերով տախտակը չի կարող անցք չպարունակել և չի կարող պարունակել երկու անցք։
Մնում է միակ հնարավոր դեպքը՝ մեկ անցքով կոշտ դասավորության դեպքը, որն էլ, ինքնաբերաբար, կլինի փոքրագույնը։ Այդպիսի դասավորության օրինակներ ցուցադրված են նկար 6-ում։ Նշենք, որ այստեղ նշված են անցքի տեղադրման բոլոր հնարավոր դեպքերը՝ пk/2, k Z պտույտի ճշտությամբ։
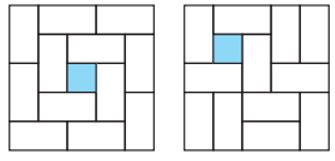
Նկար 6․ 5×5 չափսերով տախտակի փոքրագույն կոշտ շարվածքները
Այն կարելի է ապացուցել գունավորման մեթոդով։
Տախտակի բոլոր վանդակները 1 և 2 թվերով համարակալենք շախմատի տախտակի սկզբունքով, ինչպես ցույց է տրված նկար 7-ում (միջուկը վերցված է շրջանակի մեջ):
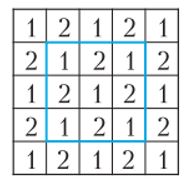
Նկար 7. Գունավորման մեթոդ
Արդյունքում կստացվի 13 վանդակ` նշված 1 թվով, և 12 վանդակ՝ 2 թվով։ Դոմինոյի յուրաքանչյուր խաղաքար ծածկում է ճիշտ մեկ վանդակ համարակալած 1-ով և մեկ վանդակ համարակալած 2-ով։ Այդ պատճառով էլ 1-ով և 2-ով ծածկված վանդակների քանակը պետք է լինի հավասար։ Այսպիսով, կոշտ շարվածքի դեպքում անցքը կարող է լինել նշված միայն 1 թվով։
Մինչ այժմ դիտարկվող տախտակների նվազագույն կոշտ շարվածքի դեպքում կա՛մ անցք չի ունեցել, կա՛մ ընդամենը մեկ անցք է պարունակել։ 6×6 չափսերով տախտակի դեպքում այս օրինաչափությունը խախտվում է։
Առաջադրանք 3. Ապացուցեք, որ 6×6 չափսերով տախտակը փոքրագույն կոշտ շարվածքի դեպքում պարունակում է ճիշտ 4 անցք։
Բերեք այդպիսի շարվածքի տարբեր օրինակներ։
Թարգմանիչ՝ Լիանա Հակոբյան
Խմբագիր՝ Մարինե Ամիրջանյան

