Աջակողմյան ձի

Հեղինակ՝ Դմիտրի Եֆիմով

Սկիզբը

Նախքան ընդհանուր դեպքին անցնելը՝ դիտարկենք շախմատի նոր խաղաքար, որին կանվանենք աջակողմյան ձի։
Շախմատի սովորական ձիուց այն տարբերվում է նրանով, որ քայլում է այսպես՝ տողով կամ սյունով երկու քայլ տեղաշարժ, իսկ հետո մեկ վանդակ դեպի աջ, տես նկար 8-ը։

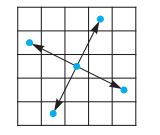
Նկար 8. Աջակողմյան ձիու թույլատրելի քայլերը

Տախտակի բոլոր այն վանդակները, որտեղ աջակողմյան ձին կարող է հայտնվել՝ սկսելով իր քայլը տրված ինչ-որ վանդակից, կանվանենք ձիու ճանապարհ, իսկ այդ ճանապարհի առանձին յուրաքանչյուր վանդակ՝ ձիու հետք։
Այստեղ և հետագայում մենք տախտակի վանդակների համար կօգտագործենք հետևյալ համարակալումը․
վանդակը, որը գտնվում է i-րդ սյան (սկսած  ձախից) և  j-րդ տողի (սկսած  ներքևից) հատման կետում,  կնշանակենք ( i, j)։ Օրինակ, նկար 9-ում, 8×8 չափսերով տախտակի վրա ցուցադրված են այն վանդակները, որտեղ կարող է հայտնվել աջակողմյան ձին՝ սկսելով իր քայլերը (1,1) վանդակից։

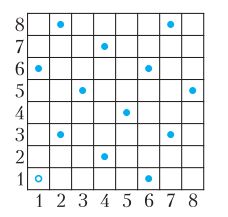
Նկար 9. Աջակողմյան  ձիու ճանապարհը տախտակի վրա

 Մաթեմատիկական  շատ խնդիրներ են առաջանում կապված աջակողմյան ձիու հետ։ Դիտարկենք դրանցից մի քանիսը։
Սահմանումից բխում է, եթե աջակողմյան ձին ( i,j ) վանդակից  կարող է հասնել ( k ,l) վանդակ, ապա նա կարող է կատարել նաև հակառակ անցումը՝ ( k ,l) վանդակից ( i,j ) վանդակ։ Դժվար չէ նկատելը  նաև, որ ձիու հետքերը պարբերաբար դասավորվում են տախտակի տողերով,  սյուներով և անկյունագծերի երկայնքով՝ 5 վանդակ ինտերվալով։ Այդ պատճառով էլ ճիշտ է հետևյալ պնդումը․

Պնդում 2.

Նշված չափսով տախտակի վրա աջակողմյան ձիու տարբեր ճանապահների քանակը  5 է։ Ընդ որում՝ յուրաքանչյուր ճանապարհ անցնում է ճիշտ մեկ անգամ յուրաքանչյուր հաջորդական 5 վանդակներով՝ տախտակի տողերով, սյունակներով և անկյունագծերով:

Հիմա դիտարկենք տրված ճանապարհի վրա ձիու հետքերի քանակի հարցը։
Պնդում 3.

Աջակողմյան ձիու հետքերի քանակը  վերևում բերված չափսի տախտակի ցանկացած ճանապարհի համար հավասար  է՝

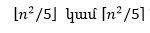
Այստեղ  այս նշանները համապատասխանաբար կլորացումն է ներքև կամ վերև մինչև մոտակա ամբողջ թիվը։

Ապացույց։ Դիցուք  տրված է վերևում նշված չափսով տախտակը։ Ենթադրենք աջակողմյան ձին սկսել է շարժումը ( 1, 1 ) վանդակից։
Պարբերականությունը հաշվի առնելով՝ բերենք ապացույցը․

Հաջորդ բոլոր տողերը հետքերի դասավորության առումով կհամընկնեն առաջին հինգ տողերից  մեկի հետ։ Այսպիսով, տախտակի վրա տրված դեպքի համար ձիու ընդհանուր հետքերի թիվը հավասար է հետևյալին՝

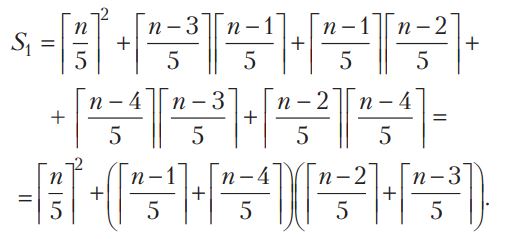
Տեղադրելով n-ի փոխարեն հաջորդաբար n=5k, 5k+1, …, 5k+4 արժեքները՝  կստանանք, որ S1-ը, կախված n-ի արժեքից, հավասար է․

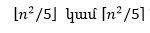
Նույն արդյունքը կստանանք, եթե ձին սկսի իր շարժումը (2,1) (3, 1), (4, 1) և (5,1) վանդակներից։ Ապացույցը թողնում ենք ընթերցողին՝ որպես վարժություն։ Պնդում 2-ի առկայությամբ այսքանը բավարար է ապացույցը ավարտելու համար։ Ակնհայտ է, որ այսպիսի արդյունքները ճիշտ են նաև ձախակողմյան ձիու համար։

Հիմնական արդյունքը

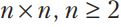
Այս բաժնում  կապացուցենք մեր հիմնական արդյունքը նշված չափսերով կամայական տախտակի համար, խաղաքարերի փոքրագույն կոշտ շարվածքի դեպքում անցքերի քանակի վերաբերյալ, ինչպես նաև կներկայացնենք փոքրագույն կոշտ շարվածք կառուցելու ընդհանուր մեթոդը։
Ակնհայտ է, որ nxn չափսերով տախտակի վրա դոմինոյի խաղաքարերի փոքրագույն քանակը ու կոշտ շարվածքի դեպքում անցքերի մեծագույն քանակը կապված են հետևյալ բանաձևով՝                      

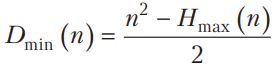
Թեորեմ։ Անցքերի մեծագույն քանակը կոշտ շարվածքի համար որոշվում է հետևյալ հավասարությամբ`

Ապացույց։

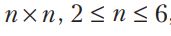
Նշված չափսերով տախտակի համար դոմինոների փոքրագույն  կոշտ շարվածքի դեպքը մենք արդեն դիտարկել ենք, և կարելի է անմիջապես ստուգել, որ  այս դեպքերում  թեորեմը ճիշտ է։
Հետագայում, հարմարության համար կդիտարկենք (n+2)x(n+2) չափսերով տախտակը։
Այդպիսի տախտակի միջուկի չափսերը կլինեն n x n ։ Միջուկում անցքերը դասավորենք աջակողմյան ձիու հետքի ինչ-որ  ճանապարհի համապատասխան։
Հետո դոմինոյի խաղաքարերը տեղադրենք  տախտակի վանդակներում անցքերի շուրջ այնպես, ինչպես ցույց է տրված նկար 10-ում։

Նկար 10․ Վանդակների տրոհումը, անցքերի շրջափակումը

 Որից հետո, անցքերի համար «վերապահված» վանդակներից բացի, չծածկված կմնան տախտակի եզրագծի միայն մի քանի վանդակներ, և հնարավոր է մի քանի վանդակներ էլ միջուկի անկյուններում։  Ընդ որում, ինչպես գիտենք, երկու հարևան անցքերի միջև տողերով և սյուներով  կլինի միջանկյալ  չորս  վանդակ։
Դիցուք՝ միջուկի եզրով  երկու հարևան անցքեր ունեն (к, n+1) և (k+5,n+1) կոորդինատները։
Այդ դեպքում տախտակի եզրին (k+2, n+2) և (k+3, n+2) կոորդինատներ ունեցող երկու վանդակներ կմնան չծածկված։
 Դրանք կարելի է ծածկել մեկ խաղաքարով, տես նկար 11-ը։

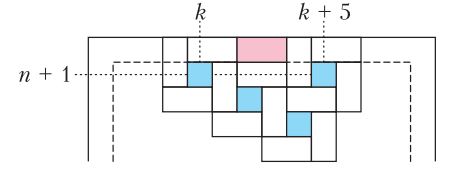
Նկար 11. Շարվածքը տախտակի եզրով

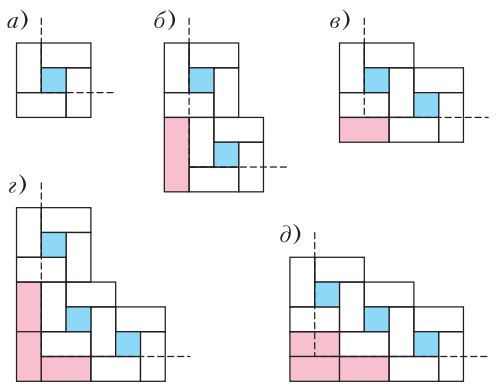
Նկար 12. Անցքերի հնարավոր փոխադարձ դասավորությունները  տախտակի եզրով

Այսպես ծածկելով տախտակը ամբողջ եզրագծով՝ մենք կթողենք չծածկված միայն տախտակի անկյունային վանդակները։
Դժվար չէ տեսնելը, որ տախտակի անյուններում հնարավոր է անցքերի դասավորության միայն հինգ տարբերակ։ Բոլորն էլ ներկայացված են նկար 12-ում (կետագծերով նշված գիծը ցույց է տալիս տախտակի միջուկի եզրը)։
Բոլոր դեպքերում, բացի բ) տարբերակից, տախտակի չծածկված վանդակները կարող են ամբողջովին ծածկվել խաղաքարերով։
Դիցուք n=5k, ապա դժվար չէ տեսնելը, որ եթե սկսենք տախտակի վրա դասավորել անցքերը՝ սկսելով (2, 2) վանդակից, ապա տախտակի անկյունները կլինեն համապատասխանաբար  a), в), г), д) տարբերակների նման, տես նկար 13-ը։ Քանի որ անկյան տեսակը  միարժեքորեն որոշվում է տրված անկյուններից ցանկացածով, ապա  կունենանք նմանատիպ իրավիճակ, եթե  անցքերը սկսենք դասավորել (4, 2 ) , (  5, 2)  և (6, 2) վանդակներից։

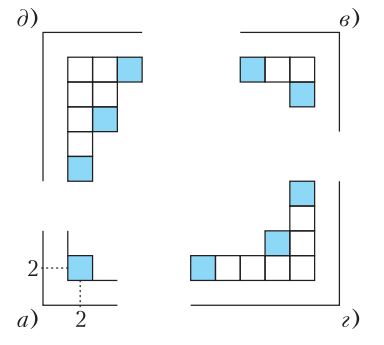
Նկար 13. Անցքերի դիրքը n=5k տախտակի անկյուններում

Այսպիսով, տվյալ դեպքում կարող ենք կառուցել կոշտ շարվածք։ Նույն ձևով կարելի է ցույց տալ, որ n = 5k + p, p = 1, 2, 3, 4 դեպքերում դիտարկվող տեսակի կոշտ շարվածքներ գոյություն ունեն։
Այս պնդման ապացույցը առաջադրանքի տեսքով նորից թողում ենք ընթերցողին։  Ընդ որում, պնդում (2)-ի համաձայն՝ անցքերի քանակը բոլոր այդ շարվածքներում փոքր չէ 

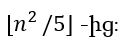
Այսպիսով, ցույց տվեցինք ու ապացուցինք, որ՝

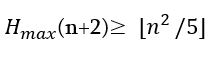
Այժմ ապացուցենք, որ՝

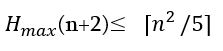
Դիցուք տրված է  10kx10k չափսերով տախտակ, նրա միջուկը համապատասխանաբար կլինի (10k-2)x(10k-2) չափսերով։ Այդ չափսերով միջուկը կարելի է ծածկել (10k-1)(10k-1) հատ 2×5 չափսի, 2k-1 հատ  5×3 չափսի ուղղանկյուններով և 3×3 չափսի քառակուսով։
Օրինակ՝ 8×8 չափսերով միջուկը կարելի է ծածկել այնպես, ինչպես ցույց է տրված նկար 14-ում։

Նկար 14. Միջուկի տրոհումը 8×8 չափսերով ուղղանկյունների և քառակուսիների

Հիշելով  անցքերի քանակի սահմանափակումները այսպիսի ուղղանկյան և քառակուսու կոշտ  շարվածքի  համար՝ ստանում ենք, որ 10k x10k չափսերով տախտակի համար ցանկացած կոշտ շարվածք  պարունակում է ոչ ավելի, քան ներքոհիշյալ չափով անցք․

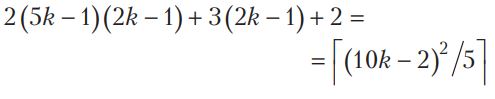
Ստուգումը թողում ենք ընթերցողին՝ որպես վարժություն։
Այսպիսով՝

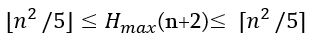
Հաշվի առնելով (1) պնդումը՝ կստանանք․

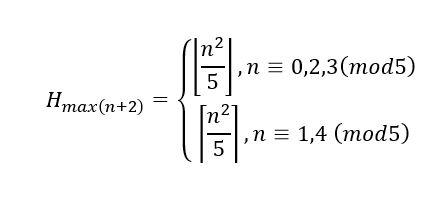
ինչը համարժեք է թեորեմի պնդմանը։
Վերջում վերադառնանք այն խնդրին, որը մեր հոդվածի սկզբում էր։
Տեղադրելով n=8 (1), (2) բանաձևերում՝ կստանանք․

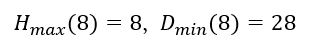
Այսպիսով, ստանդարտ շախմատի տախտակի համար փոքրագույն կոշտ շարվածքը  պահանջում է դոմինոյի ամբողջ  հավաքածուն, և առաջարկված լուծումը օպտիմալ է։

Եզրակացություն
Մենք վերլուծեցինք n x n չափսերով տախտակի վրա դոմինոյի նվազագույն կոշտ շարվածքի դեպքը։
 Այն կարելի է դիտարկել որպես հետաքրքրաշարժ գլուխկոտրուկ, բայց, հավանաբար, այստեղ ներկայացված առարկաներն ու հասկացությունները ի վերջո կիրառություն կգտնեն հետաքրքրաշարժ մաթեմատիկայի սահմաններից դուրս: Այս խնդիրը կարելի է ընդհանրացնել բնական ճանապարհով։ Դոմինոյի խաղաքարերի փոխարեն կարելի է վերցնել այլ տեսքի, այլ չափի  հարթ պատկերներ։ Քառակուսաձև տախտակի փոխարեն կարելի է օգտագործել այլ ձևի տախտակներ։
Վերջապես կարելի է անցում կատարել  այլ չափսերի և դիտարկել օրինակ «աղյուսների» կոշտ շարվածքը «արկղերում»։

Գրականություն

1. Ի․ Ակուլիչ, «Մաթեմատիկա 6-8» մրցույթ, «Քվանտ», 1991, № 10
2. Ն․ Պանյունին, Փաթեթավորումներ և ծածկույթներ, «Քվանտ», 1991, № 10
3. Ս․ Տաբաչնիկով, Դ․ Ֆուկս, Անհնարին տրոհումներ, «Քվանտ» 2011, № 2

Թարգմանիչ՝ Լիանա Հակոբյան
Խմբագիր՝ Մարինե Ամիրջանյան