Հավասարումներն են մտածում մեր փոխարեն

Квант, 1981, N 9

Ֆիզիկայի ցանկացած հաշվարկային խնդրի լուծումը բաղկացած է երկու մասից՝ ֆիզիկական և մաթեմատիկական։

Ֆիզիկոսներ ենք, քանի դեռ մտածում ենք խնդրի պայմանների մասին, վեր ենք լուծում, թե ֆիզիկական ինչ օրենքների համաձայն է տեղի ունենում տվյալ երևույթը, և կազմում ենք համապատասխան հավասարումների համակարգ։ Դրանից հետո ֆիզիկան ժամանակավորապես մղվում է երկրորդ պլան։ Հիմա մաթեմատիկոսներ ենք և բախվում ենք այլ խնդիրների՝ ինչպե՞ս առավել խելամիտ ճանապարհով լուծել ստացված հավասարումների համակարգը և գտնել պատասխանը։ Ընդ որում, պատասխանը պետք է գտնել ընդհանուր (տառային) տեսքով, այնպես որ հավասարության նշանի ձախ կողմում լինի  միայն որոնվող մեծությունը (տառային նշումով), իսկ աջ կողմում՝ միայն հայտնի մեծությունների համադրություն (նույնպես համապատասխան տառային նշանակումներով): Երբ պատասխանը արդեն ընդհանուր (տառային) տեսքով ստացվել է, կրկին դիմում ենք ֆիզիկային․ նախքան թվային տվյալներ տեղադրելը պետք է ստուգել որոնվող մեծության չափողականությունը և վերլուծել պատասխանը ճշմարտանմանության տեսանկյունից: Եթե չափողականությունը ճիշտ է, և պատասխանը՝ ճշմարտանման, կարելի է տեղադրել տվյալները և հաշվարկել։

Լուծման նկարագրված փուլերը գործնականում բնորոշ են գրեթե բոլոր խնդիրներին։ Սակայն երբեմն (հենց նման դեպքերի մասին է պատմում հոդվածը), հաշվարկներից հետո ստացվում է անսպասելի և անիմաստ արդյունք, ինչը վկայում է սխալ լուծման մասին։ Նման բան կարող է պատահել, օրինակ, երբ ո՛չ խնդրի պայմանը, ո՛չ ինտուիցիան, ո՛չ  առողջ միտքը հստակ ցույց չեն տալիս, թե որ ուղղությամբ է ընթանում գործընթացը կամ որն է վերջնական արդյունքը։

Նման խնդրի լուծմանը անցնելիս ստիպված ենք որևէ տարբերակ ենթադրել և այդ ենթադրության հիման վրա կազմել հավասարումների համակարգ։ Եթե պատասխանը անհեթեթ է, պետք չէ հուսահատվել։ Պարզապես բախտներս չբերեց․ մեր ենթադրությունն էր սխալ։Այնուամենայնիվ, որոշակի տեղեկություն ստացանք՝ տվյալ ուղղությամբ պետք չէ աշխատել։ Ինչ արած, մի այլ տարբերակ դիտարկենք և այդպես շարունակ։.Այդպիսով, խնդիրը վերածվում է փոքրիկ հետազոտության, իսկ հավասարումներն՝ ասես «մտքի ընկերների»։ Վերջապես, նրանք մեզ չեն հիասթափեցնի (իհարկե, եթե մենք էլ նրանց չհիասթափեցնենք՝ չսխալվենք հավասարումները կազմելիս և լուծելիս) և կբացահայտեն  գործընթացի իրական ուղղությունը կամ դրա վերջնական արդյունքը։

Դիտարկենք մի քանի խնդիր։

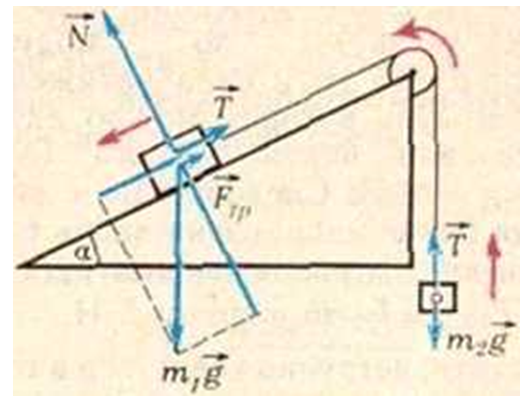
Խնդիր 1. Թեք հարթակի գագաթին ամրացված է ճախարակ, որի վրայով թել է անցնում  (Նկ. 1): Թելի ծայրերին ամրացված են երկու մարմին՝ m₁ = 3 կգ և m₂ = 2 կգ զանգվածներով։ Գտեք համակարգի արագացումը և առաջին մարմնի և հարթության միջև շփման ուժը, եթե շփման գործակիցը µ = 0.5 է, իսկ հարթության թեքության անկյունը հորիզոնի նկատմամբ՝ a = 30°:

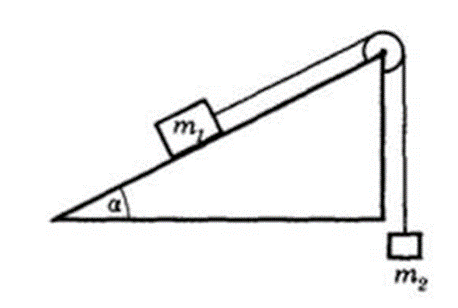
Ո՞ր ուղղությամբ է շարժվում համակարգը, և արդյոք այն ընդհանրապես շարժվո՞ւմ է։ Խնդրի ձևակերպումից պարզ չէ։ Դա իմանալը շատ կարևոր է։ Եթե համակարգը շարժվում է, ապա գործում է սահքի շփման ուժ, և  այդ ուժի մոդուլը հավասար է F_շփ = µN-ի (N-ը հայազդման ուժի մոդուլն է)։ Եթե համակարգը անշարժ  է, առաջին մարմնի վրա ազդում է դադարի շփման ուժը, որի մասին հայտնի է, որ այն չի գերազանցում սահքի շփման ուժին։

Գուցե ինտուիցիան օգնի՞։ Մի կողմից, առաջին մարմինը երկրորդից ծանր է, բայց մյուս կողմից էլ, երկրորդ մարմինը կախված է օդում, իսկ առաջինը գտնվում է թեք հարթության վրա, և կա շփում։ Ո՛չ, ինտուիցիան մեզ չի օգնի, վերլուծություն է պետք։ Փորձենք մեր մտորումները փոխանցել հավասարումներին։

Ենթադրենք, որ ճախարակը պտտվում է ժամացույցի սլաքի ուղղությամբ, այսինքն՝ երկրորդ մարմինը իջնում ​​է արագանալով, իսկ առաջինը նույն մոդուլային արագացմամբ բարձրանում է թեք հարթակով։ Պատկերենք յուրաքանչյուր մարմնի վրա ազդող ուժերը (տե՛ս նկարը),

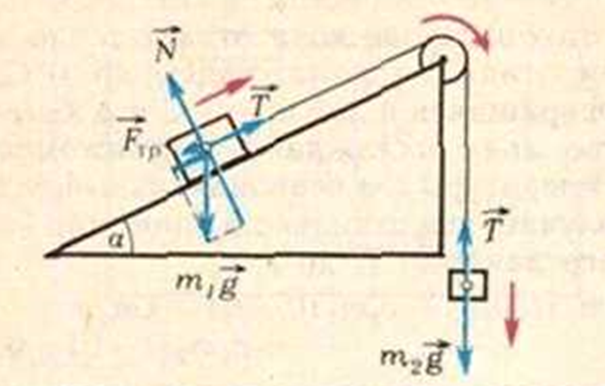
և կազմենք Նյուտոնի երկրորդ օրենքի հավասարումների համակարգը՝ համապատասխան ուղղություններով (առաջին մարմնի համար՝ թեք հարթության երկայնքով և դրան ուղղահայաց ուղղություններով, իսկ երկրորդ մարմնի համար՝ ուղղաձիգ ուղղությամբ)։

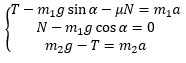
Հավասարումների համակարգը լուծելով՝

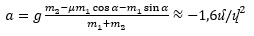
ստանում ենք, որ արագացման պրոյեկցիան ընտրված ուղղությամբ բացասական է։ Այսինքն՝ մեր ենթադրությունը սխալ է։ Այդ դեպքում ի՞նչ է կատարվում համակարգի հետ։ Շարժվում է հակառա՞կ ուղղությամբ։ Իսկ ի՞նչ արագացմամբ։

Այստեղ շատերը սխալվում են՝ կարծելով, թե համակարգը պարզապես շարժվում է հակառակ ուղղությամբ՝ նույն մոդուլային արագացմամբ ( 1,6 м/с²)։ Երբեմն, իսկապես, կարելի է այդպես համարել։ Օրինակ՝ եթե համակարգում շփման ուժ չլիներ, շարժման ուղղությունը փոխելիս բոլոր ուժերի պրոյեկցիաները կփոխեին իրենց նշանը, և արագացման մոդուլը կմնար նույնը՝ միայն հակառակ նշանով։

Սակայն այս դեպքում շփման ուժ գոյություն ունի, և երբ նոր ենթադրությամբ անցնենք հակառակ ուղղությամբ շարժմանը, շփման ուժի պրոեկցիան, ի տարբերություն մնացած ուժերի, չի փոխի իր նշանը․ այն կմնա բացասական (տե՛ս նկարը), այդ պաճառով էլ հավասարումների համակարգը ուրիշ կլինի՝

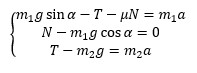
Այստեղից՝

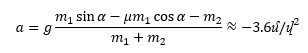
Եվ կրկին արագացման պրոեկցիան բացասական ստացվեց։ Այսպիսով, նոր ենթադրությունն էլ է սխալ։

Այսպիսով, մեր փոխարեն հավասարումները «մտածեցին» և հանգեցրին եզրահանգման, որ համակարգը չի արագանում, այսինքն՝ a=0։

Նշանակում է, որ շփման ուժը, կամ ավելի ճշգրիտ՝ դադարի շփման ուժը գտնելու համար չի կարելի օգտագործել Fշփ = µN բանաձևը, որը ճիշտ  է սահքի շփման ուժի համար։

Անհրաժեշտ  ուժը որոշելու համար պետք է դիտարկենք, թե էլ որ ուժերն են (կամ դրանց պրոեկցիաները) ազդում առաջին մարմնի վրա՝ թեք հարթության  ուղղությամբ։

Այդ ուժերից են՝ ծանրության ուժի պրոեկցիան, որը, ըստ բանաձևի, հավասար է և թելի լարվածության ուժը, որի մոդուլը կարելի է գտնել երկրորդ մարմնի անշարժ լինելու դեպքում՝Т = m₂g = 20 Ն։

Հետևաբար, դադարի շփման ուժն ուղղված է հարթության երկայնքով դեպի ներքև և մոդուլով հավասար է՝

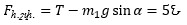
Ի դեպ, դժվար չէ համոզվել, որ այս դեպքում շփման ուժը

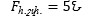
իրոք ավելի փոքր է։

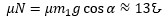
Խնդիր 2.
Կալորիաչափի մեջ, որը պարունակում է m₁=3 կգ սառույց՝ t₁=−10∘ C ջերմաստիճանով, լցվում է m₂=2 կգ ջուր՝ t₂=80∘C ջերմաստիճանով։ Ի՞նչ ջերմաստիճան կհաստատվի ջերմափոխանակության արդյունքում։ Կալորիաչափի ջերմունակությունը անտեսել։

Պարզ է, որ վերջնական t ջերմաստիճանը կգնվի -10-ից մինչև   + 80°C միջակայքում՝ — 10°C < t < 80°C։

Հետևաբար հնարավոր է, որ վերջնական ջերմաստիճանը.

• մեծ լինի 0°C-ից՝ սառույցի հալման ջերմաստիճանից
• փոքր լինի 0°C-ից
• լինի 0°C

Նախապես ասել հնարավոր չէ, թե որ տարբերակը կլինի։ Այդ իսկ պատճառով նպատակին կմոտենանք «շոշափելով»՝ փորձելով հնարավոր տարբերակները և հույսը դնելով հավասարումների «կամքի» վրա»։

Ենթադրենք, որ t>0°C, այսինքն՝ կալորիչափում միայն ջուր է։ Այս դեպքում սառույցը ջերմություն է ստանում երեք փուլով՝ մնալով սառույց, տաքանում է -10-ից մինչև 0°C՝ վերածվելով 0°C-ի ջրի և, լինելով արդեն ջուր, տաքանում է 0°C-ից մինչև t։ Այս ընթացքում ջուրը ջերմություն է տալիս միայն սառելիս՝ t₂ ջերմաստիճանից մինչև t։ Կազմենք համապատասխան ջերմային հավասարակշռության հավասարումը․

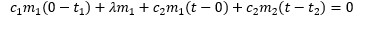
որտեղ՝

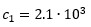
Ջ/(կգ*Կ) и c₂ = 4,2 • 10³ Ջ/(կգ*Կ)-ն սառույցի և ջրի տեսակարար ջերմունակություններն են, իսկ  = 3,4 • 10⁵ Ջ/կգ-ն՝ սառույցի հալման տեսակարար ջերմունակությունը։ Այստեղից գտնում ենք․

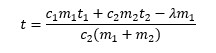
Տեղադրելով թվային արժեքները՝ ստանում ենք , որ  t<0°С։

Այսինքն՝ մեր ենթադրությունը սխալ էր։

Հիմա ենթադրենք, որ t<0°C: Այս դեպքում ջուրը ջերմություն է արձակում երեք փուլով՝ սառելով մինչև 0°C, վերածվելով սառույցի 0°C-ում և սառույցի տեսքով սառելով մինչև ցանկալի t ջերմաստիճանը, իսկ սկզբնական սառույցը ջերմություն է ստանում միայն մեկ փուլով՝ տաքանալով t₁-ից մինչև t:

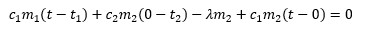
Լուծելով այս հավասարումը, կստանանք՝

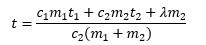
Թվային արժեքները տեղադրելով՝ համոզվում  ենք, որ  t>0° С. Հետևաբար, մեր երկրորդ ենթադրությունը նույնպես սխալ էր։

Մնում է միայն հետևյալ տարբերակը՝ t = 0° C: Սա էլ  կլինի  խնդրի պատասխանը։

Այստեղ ընթերցողի մոտ որոշակի զարմանք ու գուցե նույնիսկ դժգոհություն կարող է առաջանալ. ինչո՞ւ  է  հեղինակը դիտավորյալ ընտրում օրինակներ, որտեղ բոլոր նախնական ենթադրությունները սխալ են լինում, և բավական բարդ ու երկար լուծումներից հետո ստացվում են համեմատաբար պարզ արդյունքներ՝ a=0, t=0∘C: Ինչու՞ հենց սկզբից չէինք կարող ենթադրել  այդ պարզ տարբերակները։

Այդպիսի ճանապարհը, իհարկե, հնարավոր է, բայց այն որևէ թեթևացում չի խոստանում: Օրինակ՝ առաջին խնդրում, եթե ենթադրենք, որ համակարգը հանգստի վիճակում է, սակայն չունենանք հանգստի շփման ուժի հստակ բանաձևը, ստիպված կլինենք կազմել երեք հավասարումներից բաղկացած հավասարակշռության համակարգ՝ ուժերի բաղադրիչներով։ Սակայն այդ համակարգը լուծելուց և շփման ուժը գտնելուց հետո պարտադիր է ստուգել՝ արդյո՞ք այդ ուժն իսկապես փոքր է սահքի շփման ուժից։ Եթե ​​պարզվի, որ այդպես չէ, ապա ստիպված կլինեք վերը նկարագրված ամբողջ լուծումը սկսել սկզբից։

Երկրորդ խնդրի դեպքում, ենթադրելով t=0°C, մենք պետք է այն հաստատենք ջերմային հաշվեկշռի հավասարմով, բայց հայտնի չէ, թե ինչպես այն կազմել։ Մենք չգիտենք, թե ինչն է առաջինը զրոյի հասել՝ «ներքևից» եկած սառույցը, թե՞ «վերևից» եկած ջուրը, և որպես հետևանք՝ սառույցի մի մասը (և որ մասը) հալվե՞լ է, թե՞ ջրի մի մասը սառել է։ Իհարկե, կրկին կարող ենք ինչ-որ բան ենթադրել, բայց տարբերակների քանակը կլինի ոչ պակաս և նույնիսկ ավելին, քան վերևում տրված լուծման մեջ է։

Խնդիր 3.

Գտեք հոսանքները նկարում պատկերված շղթայի բոլոր ճյուղերում։ Այստեղ E₁ = E₂ = E = 1 В,r₁ =r₂ = r = 1 Ом И R₁ =R₂=Rз=R = 10 Ом.

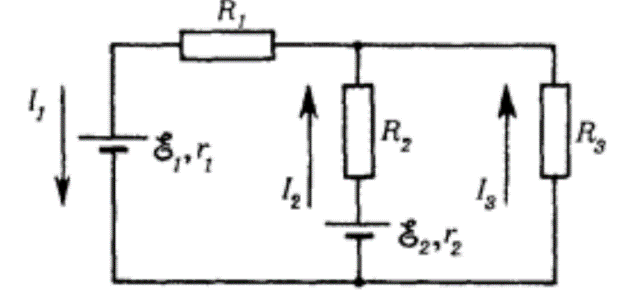
Ենթադրենք, որ I₁, I₂ և I₃ հոսանքները ուղղված են այնպես, ինչպես ցույց է տրված նկարում, չնայած դա հաստատ չգիտենք։ Եթե սխալվենք, համապատասխան հավասարումները կուղղեն մեզ։ Քանի որ էլեկտրական լիցքը չի կուտակվում ճյուղավորման կետերում (հանգույցներում), հանգույց մտնող լիցքը ժամանակի միավորում հավասար է հանգույցից նույն ժամանակահատվածում դուրս եկող լիցքին, այսինքն՝

I₁=I₂+I₃

Այս սխեմայում ընտրենք երկու պարզ փակ շղթաներ, օրինակ՝ ձախ և աջ, և ընտրենք դրա յուրաքանչյուր շղթայում շրջանցման ուղղությունները, օրինակ՝ ժամացույցի սլաքի հակառակ ուղղությամբ: Էներգիայի պահպանման օրենքի համաձայն՝ ԷլՇՈՒ-ների հանրահաշվական գումարը հավասար է լարման անկումների հանրահաշվական գումարին․

E-E=I₁R+I₁r+I₂r+I₂R

-E=-I₂R-I₂r+I₃R

Ստացված հավասարումները միավորենք համակարգի մեջ և, պարզության համար, տեղադրենք թվային տվյալները․

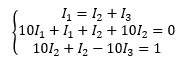
 Լուծելով այս համակարգը՝ ստանում ենք հոսանքների արժեքները․

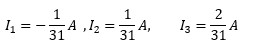
Այսինքն՝ առաջին և երրորդ հոսանքների նշանները բացասական են, ինչը վկայում է, որ մեր նախնական ենթադրած ուղղությունները սխալ էին։ Մենք թվային արժեքները ճիշտ գտանք, բայց այդ հոսանքների ուղղությունները հակառակ են ենթադրյալներին։

Խնդիր 4.

Մարմինը ուղղահայաց վեր է նետված v₀ = 25 մ/վ սկզբնական արագությամբ: Որքա՞ն ժամանակ անց այն կգտնվի h = 40 մ բարձրության վրա:

Գրենք ուղղաձիգ վեր նետված մարմնի կոորդինատի հայտնի բանաձևը (դրական համարում ենք դեպի վեր ուղղությունը):

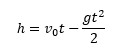
Լուծելով այս հավասարումը  t-ի համար՝ կստանանք՝

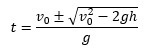
Սակայն, թվային տվյալները տեղադրելիս պարզվում է, որ արմատի տակ գտնվող արտահայտությունը բացասական է։ Ի՞նչ է սա նշանակում։

Պարզվում է, որ այս հավասարումը իր լեզվով մեզ ասում է, որ այս մարմինը ընդհանրապես նման բարձրության չի հասնում։ Իրականում, վերելքի առավելագույն բարձրությունը

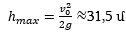
որը փոքր է h =40 մ-ից։

Այսպիսով, լինում են դեպքեր, երբ հավասարումները մեր փոխարեն անսպասելիորեն, չպլանավորված  են «մտածում»։

Անգլիացի բնագետ Թոմաս Հաքսլին մի անգամ մաթեմատիկան համեմատել է ջրաղացաքարերի հետ, որոնք աղում են միայն այն, ինչ լցվում է դրանց մեջ և ոչ ավելին։Բերված օրինակները ցույց են տալիս այդ  միտքը. եթե հավասարման մեջ սխալ գաղափար է դրվել, լուծումը «թեփ» կլինի, և մեզ կմղի բանական  «հատիկ» գտնելու։

Վարժություններ

1. m = 10 կգ զանգվածով համասեռ լծակը հենված է իր ձախ ծայրից l₁ = 25 սմ հեռավորության վրա գտնվող հենարանին: Լծակի երկարությունը l = 1 մ է և m₁ = 2 կգ զանգվածով բեռը կախված է լծակի ձախ ծայրից: Ի՞նչ ուժով պետք է ազդվի աջ ծայրի վրա՝ a = 30° անկյան տակ հորիզոնի նկատմամբ, որպեսզի լծակը  լինի հավասարակշռված։

2․ Կալորիչափի մեջ, որտեղ գտնվում է t₁ ​=0^∘C ջերմաստիճանի m₁=1 կգ սառույց, ներարկում են  t₂=100^∘C ջերմաստիճանի m₂=500 գ զանգվածով ջրի գոլորշի։ Ջերմափոխանակության ավարտից հետո ի՞նչ ջերմաստիճան կլինի։ Կալորիաչափի ջերմունակությունը կարելի է անտեսել։

3. Մարմինը ուղղաձիգ վեր է նետված v₀=15 մ/վ սկզբնական արագությունով: Ի՞նչ ճանապարհ կանցնի այն t=2 վ թռիչքի ընթացքում: Ազատ անկման արագացումը համարվում է g=10 մ/վ²:

Ռուսերենից թարգմանեց Իննա Իսրայելյանը։