Մաթեմատիկայի ուժը

Հոդվածը մաթեմատիկայում պարզ գաղափարների ուժի մասին է։ Ահա, թե ինչ եմ սիրում անել․  վերցնել այն, ինչը հասկանալը մնացածների համար բարդ  ու դժվար է, և գտնել պարզ մի գաղափար, որը թույլ կտա ցանկացած մեկին (նաև քեզ) պարզաբանել այդ բարդությունը։

Այս պարզ գաղափարները կարող են զարմանալիորեն հզոր լինել, բայց դրանք գտնելը ևս զարմանալիորեն դժվար է։

Շատ անգամ պարզ գաղափարներ գտնելու համար պահանջվում է մեկ դար կամ ավելին։ Իրականում հաճախ անհրաժեշտ էր լինում երկու հազարամյակ․ այս գաղափարը կարող էին բացահայտել հին հույները, բայց չբացահայտեցին։

Տարածված է սխալ պատկերացում, որ այն, ինչ արեցին Այնշտայնի նման մարդիկ, բարդ էր: Ո՛չ, իրականում աշխարհը ցնցում են պարզ գաղափարները։ Բայց այս գաղափարների մեջ կա նրբություն, որը խանգարում է մարդկանց մտածել դրանց մասին։ Պարզ գաղափարը պարունակում է մի հարց, որը ոչ մեկի մտքով չի անցնում տալ։

Դիտարկենք այս հարցը՝ Երկիրը կլո՞ր է, թե՞ հարթ։ Արդյո՞ք հին մարդիկ նստած մտածում էին. «Հիմա տեսնենք Երկիրը գո՞ւնդ է, թե՞ հարթություն»: Ո՛չ, ես կարծում եմ, որ ոչ ոք իրականում չէր կարող պատկերացնել, որ Երկիրը գնդաձև է, եթե ինչ-որ մեկը չնկատեր, որ աստղերը մայր են մտնում արևմուտքում և տասներկու ժամ անց ծագում արևելքում, ու չառաջարկել, որ ամեն ինչ կարող է շրջանաձև շարժվել, ինչը դժվար է համապատասխանացնել Երկրի՝ հարթ լինելու ընդունված պատկերացումին։

Մեկ այլ տարօրինակ գաղափար կապված է «վերև» հասկացության հետ։ Արդյո՞ք  բացարձակ է այս հասկացությունը։ Այդպիսին է եղել Արիստոտելի ֆիզիկայում։ Միայն Նյուտոնի ֆիզիկայում է գիտակցվել, որ «վերև» հասկացությունը հարաբերական է. այն, ինչ մեկի համար ուղղված է «վերև», մյուսի համար ուղղված է «ներքև» (օրինակ, եթե մեկը գտնվում է Քեմբրիջում, մյուսը Ավստրալիայում է): Էյնշտեյնը ստեղծեց հարաբերականության տեսությունը, երբ գիտակցեց նմանատիպ փաստ ժամանակի բնույթի  մասին ․ այն, ինչ մեկի համար բաժանված է ժամանակի մեջ, մյուսի համար կարող է բաժանվել միայն տարածության մեջ։

Եկեք խոսենք ավելի հասկանալի բաների մասին։ Ես կցանկանայի ձեզ ներկայացնել մի քանի պարզ գաղափարներ, որոնք կապված են քառակուսիների, եռանկյունների և հանգույցների հետ:

Քառակուսիներ

Սկսենք հին թեորեմի նոր ապացույցից։ Հարցը հետևյալն է․ «Արդյո՞ք քառակուսու անկյունագիծը համաչափ է իր կողմին»: Կամ ժամանակակից տերմինաբանության մեջ. «Հանդիսանում է արդյո՞ք երկուսի քառակուսի արմատը երկու ամբողջ թվերի հարաբերություն»։ Այս հարցը բերեց մեծ հայտնագործության՝ իռացիոնալ թվերի հայտնաբերմանը, որը վերագրվում է պյութագորասցիներին։

Նկ․ 1

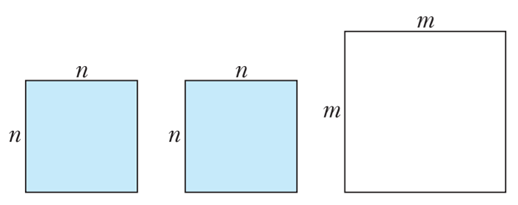
Հարցը դնենք ուրիշ կերպ (նկ․ 1)։ Կգտնվի արդյո՞ք երկու այնպիսի քառակուսի, որոնց կողմերը հավասար են ո ամբողջ թվին, իսկ նրանց մակերեսների գումարային արժեքը հավասար լինի մի քառակուսու մակերեսին, որի կողմը հավասար է մի ուրիշ m ամբողջ թվին։

Եթե m-ը և n-ը ամբողջ թվեր են, կարո՞ղ է երկու n x n չափսի կապույտ քառակուսիների մակերեսների գումարը հավասար լինել m x m չափսի սպիտակ քառակուսու մակերեսին։

Սա մոտավորապես ճշմարիտ է 12×12 չափերով քառակուսիների դեպքում։ Եթե 12-ը բազմապատկենք 12-ով, կստանանք 144, իսկ 144-ին գումարենք 144, կլինի 288, որը ճիշտ հավասար չէ  289-ին, այսինքն՝ 17×17։ Այսպիսով՝  17/12= 1,41666 շատ մոտ է

= 1,41421․․․, միայն տարբերությունը  կազմում է երկու հազարերորդականը։

Բայց մենք չենք հարցնում, թե հնարավո՞ր է գտնել այնպիսի m և n ամբողջ թվեր, որոնց համար մոտավորապես

։ Մենք ցանկանում ենք պարզել, կարող է դա լինել ճշգրիտ։

Ենթադրենք՝ հնարավոր է։ Այդ դեպքում պիտի գտնվի այդպիսի ամենափոքր m ամբողջ թիվ, որի համար դա հնարավոր է։ Գծագրենք հնարավոր ամենափոքր m -ի համար։ Տեղադրենք երկու կապույտ գույնի փոքր քառակուսիները մեծ քառակուսու վերին աջ և ստորին ձախ անկյուններում (ինչպես ցույց է տրված նկ․ 2 — ում)։

Նկ․ 2

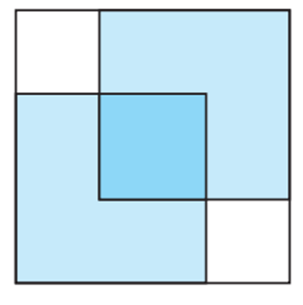
Մեծ քառակուսու մի մասը ծածկված է կրկնակի փոքր քառակուսիներով, իսկ մյուս մասը ընդհանրապես ծածկված չէ։ Նկ․ 2 -ում կրկնակի ծածկված հատվածը մուգ կապույտ գույնով է ներկված, իսկ չծածկված մասը՝ սպիտակ գույնով։ Քանի որ ի սկզբանե սպիտակ քառակուսու մակերեսը հավասար էր բաց կապույտ քառակուսիների մակերեսների գումարին, ապա կրկնակի ծածկված մասի մակերեսը ճիշտ հավասար պիտի լինի չծածկված մասի մակերեսին (նկ․ 3)։

                                                Նկ․ 3

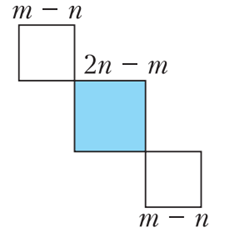
Որքա՞ն է այս երեք մասերի մակերսների գումարը։ Մուգ կապույտ մասը քառակուսի է, որի կողմը հավասար է (2n — m) ամբողջ թվին, իսկ երկու սպիտակ մասերը նույնպես քառակուսիներ  են՝ (m — n) կողմերով։ Այսպիսով, սկսած ենթադրյալ ամենափոքր m ամբողջ թվից, որի քառակուսին հավասար է ամբողջ թվի կրկնակի քառակուսուն, մենք գտանք այս հատկությամբ ավելի փոքր ամբողջ թիվ՝ (2n — m)։ Սա նշանակում է, որ ամենափոքր լուծում չի կարող լինել։ Բայց եթե լուծումներ կան, ապա դրանց մեջ պիտի լինի ամենափոքրը։ Այստեղից եզրականցնում ենք, որ լուծումներ գոյություն չունեն։ 

Սա ոչ ակնհայտ արդյունք է։ Ոչ բոլոր իրական թվերն են հանդիսանում ամբողջ թվերի հարաբերություն։ Ներկայացված նոր ապացույցը գտավ Սթենլի Թեննենբաում անունով իմ ընկերը, ով հետագայում թողեց մաթեմատիկան։

Եռանկյունիներ

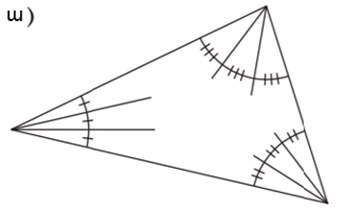
Վերցնենք ձեր ընտրությամբ ցանկացած եռանկյունի և եռահատենք նրա յուրաքանչյուր անկյունը։ Սա նշանակում է, որ մենք յուրաքանչյուր անկյուն կբաժանենք  հավասար աստիճանային չափ ունեցող անկյունների (նկ․ 4ա)։

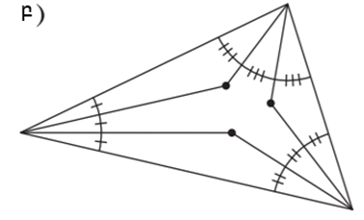
Նկ․ 4

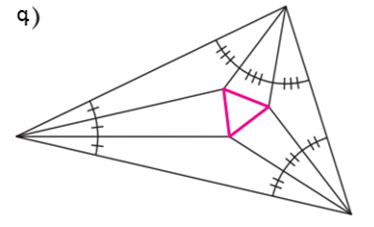
Շարունակենք տարված ճառագայթները, մինչև նրանք հատվեն երեք կետերում (նկ․ 4բ)։

Այնուհետև Ֆրենկ Մորլիի բավականին տպավորիչ թեորեմն ասում է, որ այս կետերով ձևավորված եռանկյունը հավասարակողմ է (նկ. 4գ): Եվ սա ճիշտ է ցանկացած եռանկյան համար։

Մորլիի թեորեմը համարվում է իսկապես դժվար ապացուցելի։ Շատ պարզ է ձևակերպվում, բայց շատ դժվար է ապացուցվում։ Մորլին այս արդյունքը ձևակերպեց մոտավորապես 1900 թվականին, իսկ առաջին ապացույցը հրապարակվեց մոտավորապես 15 տարի անց։ Այնուամենայնիվ, ես գտա մի պարզ ապացույց իմ ընկեր Փիթեր Դոյլի օգնությամբ։

Մորլիի թեորեմի մեր պարզ ապացույցը հետևյալն է: Առաջին հերթին նշեք ձեր սկզբնական եռանկյունու A, B, C անկյունները: Մի՛ մոռացեք, որ անկյունների գումարը պիտի 180 աստիճան լինի։ Ահա հետագա պլանը։ Ես պատրաստվում եմ սկսել ինչ-որ չափի հավասարակողմ եռանկյունուց, կառուցել նրա շուրջ 6 ուրիշ եռանկյունիներ և միացնել նրանց այնպես, որ ստանանք  A, B, C անկյուններով եռանկյուն, այնպիսին, որ հավասարակողմ եռանկյան կողմի չափի որոշակի ընտրությամբ իմ գծագիրը ճշգրիտ կվերարտադրի սկզբնական եռանկյունին։ Ավելին, իմ գծագիրը կապացուցի, որ երբ եռահատեք ձեր եռանկյան անկյունները, դուք կգտնեք իմ հավասարակողմ եռանկյունը մեջտեղում: Նկար 5-ում ներկայացված են վեց եռանկյունները, որոնք մենք կկառուցենք հավասարակողմ եռանկյան շուրջ:

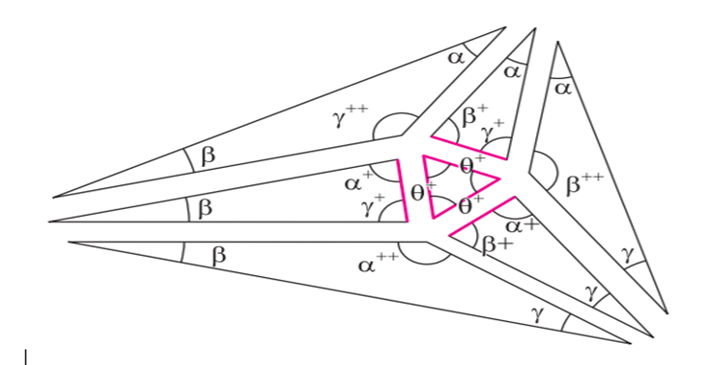
Նկ․ 5

Այս գծագիրը նման է նոր կառուցած եռանկյան բեկորների։ Եվ իսկապես, եթե միացնենք այդ մասերը ինչպես պետքն է,  կկառուցենք  ձեր եռանկյունին։ Սակայն պետք է հասկանալ, որ այս վեց նոր եռանկյունիները որոշվելու են իմ հավասարակողմ եռանկյան հիման վրա՝  օգտագործելով ձեր առաջարկած A, B և C արժեքները։ Նկար 4գ -ն մեր նպատակն է, ոչ թե ելակետը։

Վեց նոր եռանկյունիները կառուցելիս նախ որոշենք նրանց ձևը, ապա չափերը։ Ձևը որոշելու համար եկեք որոշենք անկյունները։ Ենթադրենք, α= A/ 3,      β = B/ 3 և γ= C/ 3։ Նաև կատարենք հետևյալ նշանակումները՝ եթե θ-ը կամայական անկյուն է, ապա  θ⁺ -ը նշանակում է  + 60°, իսկ θ⁺⁺-ը նշանակում է  + 120° : Այսպիսով, օրինակ՝ հավասարակողմ եռանկյան բոլոր երեք ներքին անկյունները հավասար են  60°, ապա կարող ենք նշանակել  0⁺:

Եկեք որոշենք անկյունները, ինչպես ցույց է տրված նկար 5-ում: (Դուք կարող եք ստուգել, ​​որ յուրաքանչյուր եռանկյան անկյունների գումարը 180° է:) Այժմ, որպեսզի հավասարակողմ եռանկյանը կից յուրաքանչյուր եռանկյան չափը որոշենք, դարձնենք կողմերից որևէ մեկի երկարությունը այնքան, որքան հավասարակողմ եռանկյան կողմերի երկարությունն է։ Գծագրի մեջ այդ կողմերը կարմիր են։

Այնուհետև որոշենք երեք բութանկյուն եռանկյունիների չափումները․ ես ցույց կտամ՝ ինչպես դա անել նրանցից ամենաաջ գտնվողի համար, և դուք կարող եք կիրառել նույն մեթոդը մյուս երկուսի համար։ Բութ անկյան գագաթի միջով տանենք երկու ուղիղ գիծ, որոնք հատում են ամենաերկար կողմը β⁺ անկյան տակ (որը մոտ է ուղղահայացությանը), և որոշենք եռանկյան չափը այնպես, որպեսզի գագաթից մինչև կողմ հատվածները ունենան նույն երկարությունը, ինչ հավասարակողմ եռանկյան կողմը (նկար 6)։

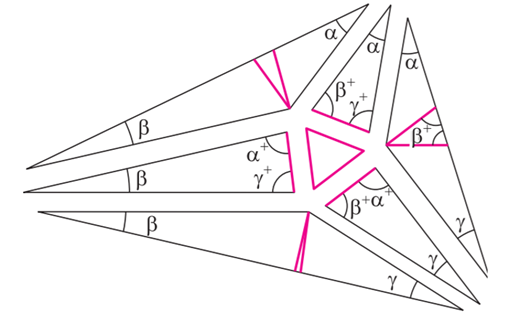
Նկ․ 6

Նման կերպ որոշելով բոլոր եռանկյունիների չափումները՝ ես հիմա պնդում եմ, որ երկու գունավորված եռանկյունիները (նկ․ 7) հավասար են՝ մեկը հանդիսանում է մյուսի սիմետրիկ պատկերը։

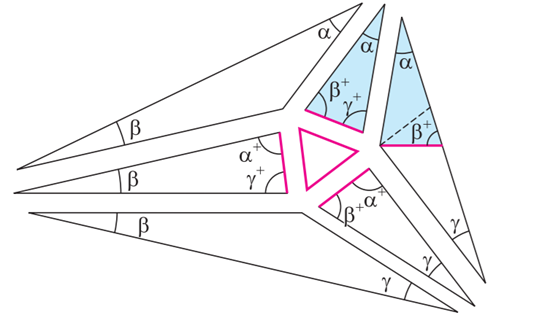
Նկ․ 7

Ինչպես տեսնում ենք,  իսկապես այդպես է, քանի որ նրանք ունեն երկու հավասար անկյուններ՝
α-ն ու β⁺ -ը, և հավասար կողմ (նկարում կարմիր է, հավասար է հավասարակողմ եռանկյան կողմին): Այդ դեպքում երկու եռանկյունիների հարակից կողմերի երկարությունները հավասար են։ Կիրառելով այդ դիտարկումները վեց անգամ՝ մենք կպարզենք, որ նկարի  բոլոր հարակից կողմերը իրար հավասար են, և դրանով իսկ կհասատատենք, որ վեց եռանկյունիները հարակից են իմ հավասարակողմ եռանկյանը, եթե միայն յուրաքանչյուր ներքին գագաթի անկյունների գումարը 360 աստիճան է: Ցանկացած ներքին գագաթի դեպքում, անկյունների գումարը հավասար է  (α⁺+ β⁺⁺ + γ ⁺ + 0⁺ ), որը 5 հատ + նշան է, որը կազմում է 300 աստիճան, իսկ α+ β+ γ , որը արդյունքում հենց տալիս է 360 աստիճան  (նկ․ 8):

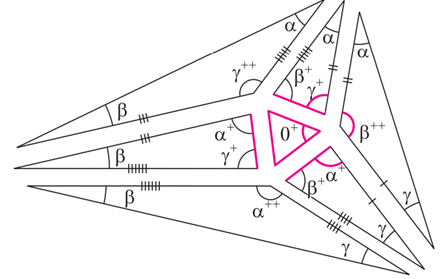
Նկ․ 8   

Արդյունքում՝ իրար միացնելով այս յոթ մասերը՝ ես ստացա ձեր անկյուներով եռանկյունը, որի համար ճիշտ է Մորլիի թեորեմը։ Հետևաբար, Մորլիի թեորեմը ճշմարիտ է ձեր եռանկյունու և ցանկացած եռանկյան համար, որը դուք կարող եք ընտրել:

Հեղինակ՝ Ջոն Կոնվեյ

Թարգմանության աղբյուրը՝ այստեղ ։

Շարունակությունը՝ այստեղ։

Թարգմանիչ՝ Մարիամ Համբարձումյան