Մաթեմատիկայի ուժը

Նախորդ մասը՝ այստեղ։

Հանգույցներ

Հիմա ցանկանում եմ մի քիչ պատմել հանգույցների տեսության և մի պարզ գաղափարի մասին, որն առաջացավ շատ տարիներ առաջ, երբ Լիվերպուլի ավագ դպրոցի աշակերտ էի։

Նախ և առաջ, ի՞նչ հետաքրքիր բան կա հանգույցներում։ Հանգույցները, կարծես, այնքան էլ մաթեմատիկական օբյեկտներ չեն։  Հանգույց ասելով հասկանանք պարանի փակ կտոր։ Առաջին հարցը, որն ակնհայտ չէ՝ գոյություն ունե՞ն պարզագույն հանգույցներից, այսինքն՝ շրջանաձևերից տարբերվող հանգույցներ։ Հնարավո՞ր է նույնիսկ շատ խճճված հանգույցը քանդել, այսինքն՝ ստանալ պարզագույն հանգույց։

Օրինակ՝ կարելի՞ է քանդել երեքնուկը (նկ․ 9)։

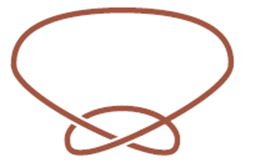
Նկ․ 9

Փաստը, որ ոչ ոք այն չի քանդել, չի նշանակում, որ չի կարելի անել, այլ նշանակում է, որ մարդիկ խելացի չեն մտածել։ Հիշենք, որ մոտ երկու հազար տարի ոչ մեկի մտքով որոշ պարզ գաղափարներ չէին անցել, իսկ հետո եկավ Այնշտայնը, ում մոտ այդ գաղափարները առաջացան։ Մինչ մենք պարանի կտորով խաղում ենք՝ մի ուրվանկարը մյուսով փոխելով, կարող է երեք հիմնական դեպք պատահել։ Դրանք կոչվում են Ռայդեմայստերի շարժումներ՝ գերմանացի երկրաչափ Կուրտ Ռայդեմայստերի անունով։ Այդ շարժումները նշանակենք R₁, R₂, R₃ (նկ․ 10)։

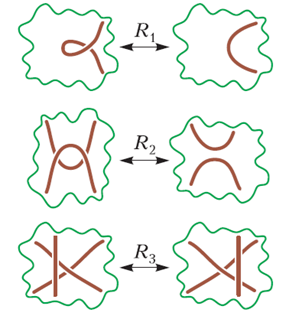
Նկ․ 10

R₁-ը մի հանգույցի ոլորելն է կամ ոլորքը քանդելը, չի փոխում մյուսները։    R₂ -ը հանգույցը խցկում է պարանի հարևան մասի տակ։ R₃— ը սահքի շարժում է , որը պարանի մի մասը անց է կացնում այն տեղով, որտեղ հանդիպում են երկու ուրիշ մասերը։

Հանգույցների բոլոր ձևափոխությունները կարելի է հանգեցնել այս երեք շարժումների հաջորդականությանը։

Իսկ կա՞ շարժումների հավաքածու, որը թույլ կտա սկսել նկար 11-ի ձախ հանգույցից  և վերջացնել աջ կողմի պարզագույն հանգույցով («չհանգույց»)։

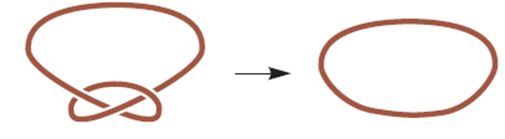
Նկ․ 11

Միգուցե կկարողանաք հորինել շարժումների հաջորդականություն, որը կբերի խճճված պատկերի, ինչպես նկար 12-ի  աջ կողմում է, բայց գուցե միլիոնավոր հատումներով։

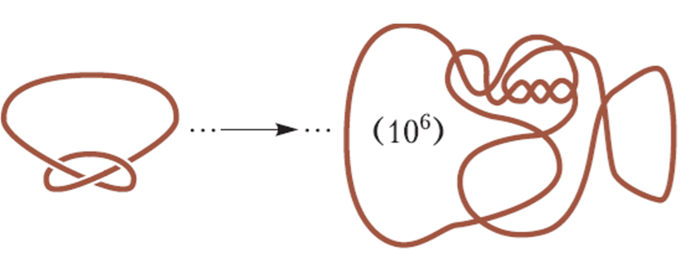
Նկ․ 12

Եվ բազմաթիվ շարժումներից հետո այն, ի վերջո, կհանգեցնի ոչ հանգույցի։

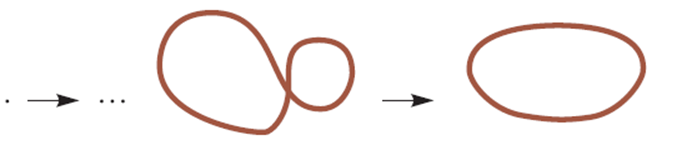
Նկ․ 13

Կարո՞ղ ենք վստահ լինել, որ նման հաջորդականություն գոյություն չունի։

Նախապես հայտնի չէ։ Ես կասկած չունեմ, որ ոչ ոք նույնիսկ չի փորձել ծածկել ուրվանկարների ամբողջ խելահեղ զանգվածը միլիոն հատումներով և պարզել, թե ինչ է տեղի ունենում յուրաքանչյուրի դեպքում։ Եվ խնդրի դժվարությունն այն է, որ եթե մենք ուզում ենք ապացուցել, որ գոյություն ունի ինչ-որ ոչ տրիվիալ հանգույց, ապա պետք է ցույց տանք, որ շարժումների ոչ մի հաջորդականություն այն չի լուծում:

Այժմ պատրաստվում եմ ներկայացնել այն, ինչ ես անվանում եմ հանգույցների համարակալում: Համարակալում ստեղծելու համար հարկավոր է թելի յուրաքանչյուր տեսանելի հատվածին համապատասխան մի փոքր թիվ նշանակել. և որտեղ մի թել թաքնված է մյուսի տակ, ստորին թելի հատվածներում երկու թվերը պետք է միացված լինեն այնպես, որ կախված լինի վերին թելի հատվածի թվից     (նկ․ 14):

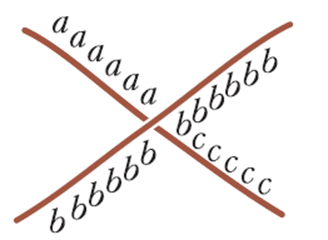
Նկար 14

Եվ իհարկե (նկ․ 14), եթե վերին թելի թիվը հավասար է b-ի, իսկ ներքևի թելի թվերը վերևից երկու կողմերում հավասար են a-ի և с-ի, ապա «a, b, c» թվերը պետք է կազմեն թվաբանական պրոգրեսիա։ Սա նշանակում է, որ աճը  a-ից b-ը  նույնն է, ինչ b-ից c-ն: Օրինակ, եթե a = 13 և b = 16, ապա c = 19 (նկ. 15):

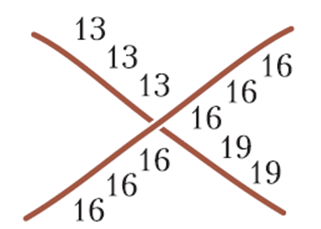
Նկար 15

Ինչի՞ համար են այս թվերը: Տեսնենք՝ արդյոք կարելի է նրանց համարակալել: Եկեք վերցնենք մեր հին ընկերոջը՝ «երեքնուկ» հանգույցը, և շրջանցենք այն՝ թվեր վերագրելով  նրա տարբեր հատվածներին և ստուգելով, թե արդյո՞ք թվաբանական պրոգրեսիայի պայմանը կարող է բավարարվել յուրաքանչյուր հատման տեղում։ Որտեղի՞ց սկսենք։

Նկատենք, որ թվաբանական պրոգրեսիայի պայմանը անփոփոխ է․ կարելի է բոլոր a, b, c թվերը տեղափոխել վերև կամ ներքև՝ ցանկացած միջակայքով, ու նրանք նույնպես կկազմեն թվաբանական պրոգրեսիա։ Այնպես, որ սկզբում դուք կարող եք նկար 16-ի որևէ հատվածը նշել 0 և 1 նշաններով, իսկ հանգույցի մնացած մասի վրա տեղադրել այն, ինչ հետևում է այս ընտրությունից: Պիտի նշենք յուրաքանչյուր խաչմերուկ՝ կիրառելով այս օրենքը։

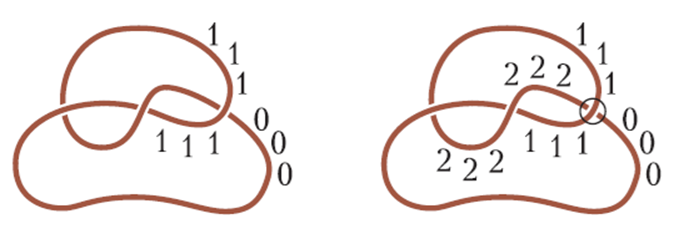
Նկար 16

Սկզբում ամեն ինչ լավ է ընթանում։ Բայց շուտով վերին հատվածում խնդիր է առաջանում (նկ. 17). 4-ը հավասար չէ 1-ի, բայց պետք է հավասար լինի, քանի որ և՛ 4-ը, և՛ 1-ը գտնվում են պարանի նույն հատվածում։

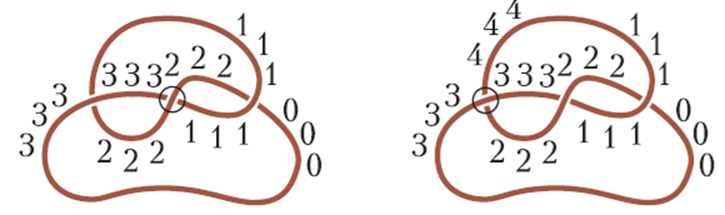
Նկար 17

Սակայն  մաթեմատիկական մեթոդների մեծ ուժը դրսևորվում է  նաև նրանում, որ  ես կարող եմ հասկացությունները սահմանել այնպես, ինչպես ուզում եմ, ուստի ես մտադիր եմ 4-ը սահմանել որպես մեկ  միավորին հավասար: (Մաթեմատիկոսներն այս հավասարությունն անվանում են «մոդուլ 3 համեմատելիություն»:) Ուռա՛։ Մեզ հաջողվեց։ Նմանատիպ հակասություն կա նաև ստորին հատվածում (նկ. 18). այն ունի երկու նշան՝ 3 և 0։ Բայց եթե 4-ը հավասար է 1-ի, ապա 3-ը հավասար է 0-ի։ Այսպիսով, ամեն ինչ կարգին է։

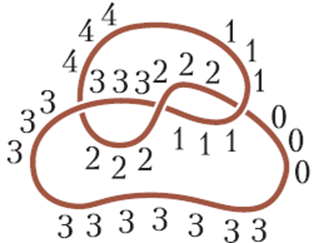
Նկար 18

Մենք ստացանք համարակալում։ Ո՞րն է նման համարակալումների իմաստը: Այն հրաշալի է: Տեսեք, թե ինչ է տեղի ունենում, երբ մենք վերցնում ենք համարակալված հանգույց և դրա վրա կիրառում ենք Ռայդեմայստերի երեք  շարժումները: Հնարավո՞ր է աջ կողմի համարակալումը ստանալ նկար 19 ա, բ և գ-ի ձախ կողմում գտնվող համարակալումից։

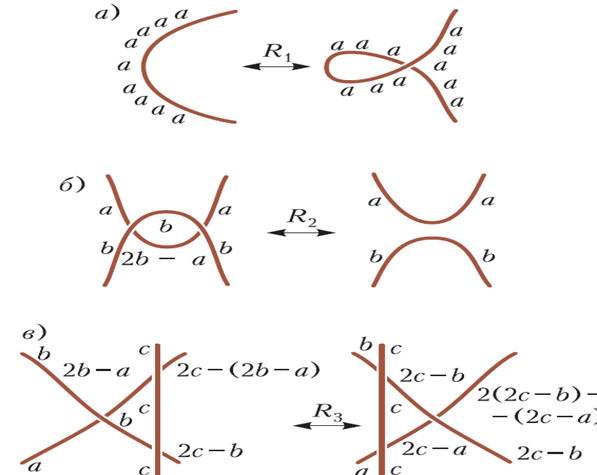
Նկար 19

Պատասխանը դրական է՝ ձախ պատկերի ցանկացած ճիշտ համարակալում կարելի է վերածել աջ պատկերի ճիշտ համարակալման, և հակառակը։ Սա բավականին հեշտ է ստուգել առաջին երկու շարժումների համար: Երրորդ շարժման համար պետք է համոզվենք, որ 2(2c — b) — (2c — a ) = 4c – 2b  — (2c — a) = 2c — (2b — a)։

Մենք տեսնում ենք, որ հնարավոր է կատարել երեք շարժումներից որևէ մեկը՝ առանց աղավաղելու մնացած համարակալումը։

Քանի որ ցանկացած ճիշտ համարակալումը ճշմարիտ է  ցանկացած ուղղությամբ շարժում կատարելիս, նկարի ձախ կողմում հնարավոր համարակալումների թիվը հավասար է աջ կողմում գտնվող համարակալումների թվին:

Վերադառնանք այն հարցին, թե արդյոք կարելի է երեքնուկը վերածել ոչ հանգույցի։ Ոչ հանգույցի համար կա ուղիղ երեք համարակալում (նկ. 20): Միևնույն ժամանակ, երեքնուկն  ունի առնվազն չորս համարակալում՝ ամենուր 0, ամենուր 1, ամենուր 2, և համարակալումը, որը ներկայացված է նկար 21-ում։

Նկար 20

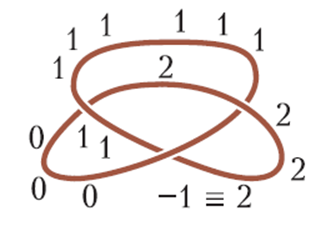
Նկար 21

Եվ հիմա մենք կարող ենք ապացուցել, որ երեքնուկը հնարավոր չէ քանդել․ այն ունի ուրիշ քանակի համարակալում, չհանգույցը՝ ուրիշ։ Եթե երեքնուկն ու չհանգույցը միացված լինեին Ռայդեմայստերի շարժումների հաջորդականությամբ, ապա նրանք կունենային  հավասար քանակով համարակալում։

Սա ապացուցում է, որ հանգույցները գոյություն ունեն։

Խճճվածքներ

Ես հաճախ ցույց եմ տալիս մի փոքրիկ հնարք, որը ներառում է հանգույցներ կապելը: Խճճվածքները չորս չամրացված ծայրերով փոքր հանգույցներ են և անսպասելի կապ ունեն թվաբանության հետ:

Խճճվածքներն ավելի լավ պատկերվում են չորս պարողների միջոցով։ Երկու պարողներ բռնում են մի պարանի ծայրերը, իսկ մյուս երկուսը՝ մյուս պարանի ծայրերը։ Կարելի է խճճվածքները   կառավարել՝ կատարելով երկու շարժում՝ ոլորել ու պտտել։

Պտտվելիս (նկ. 22) աջ կողմի երկու պարողները փոխվում են տեղերով, ընդ որում՝ ստորին պարողն անցնում է վերինի պարանի տակով։

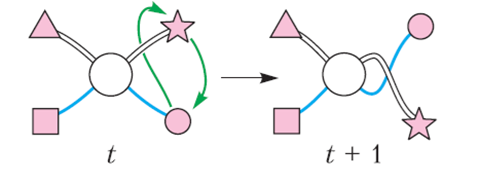
Նկար 22

Այնուհետև յուրաքանչյուր խճճվածքին կտանք որևէ թվային արժեք, և ոլորումը կփոխի այս արժեքը t-ից t +1: (Այս արժեքները կապված չեն համարակալման հետ, այժմ կարող եք մոռանալ համարակալման մասին):

Պտտվելիս (նկ. 23) բոլոր չորս պարողները  շարժվում են մեկ դիրքով՝ ժամացույցի սլաքի ուղղությամբ։ Խճուճի  արժեքը փոխվում է t -ից մինչև -1/t:

Նկար 23

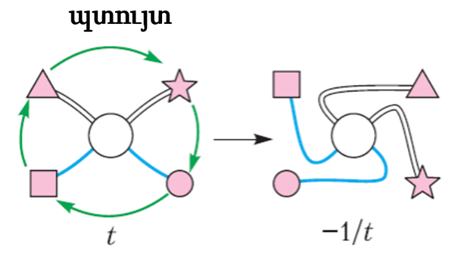
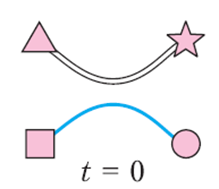
Նկար 24

Սկսենք նրանից, որ նկար 24 -ի խճճվածքին տանք t=0 արժեքը։ Դիտարկենք շարժումների կամայական հաջորդականությունը (նկ. 25): Ձեր խնդիրն է, հարգելի՛ ընթերցող, պարողներին վերադարձնել զրոյի: Բայց ձեզ թույլատրվում է անել միայն այն երկու շարժումները, որոնց մասին ես խոսեցի։ Ցանկանում եք պտտվե՞լ, թե՞ շրջվել:

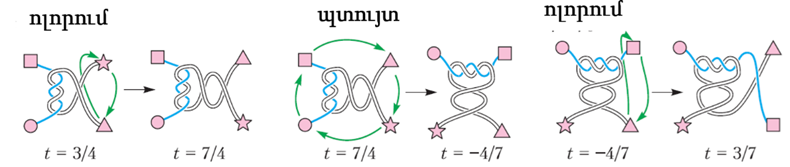
Դուք կգտնեք, որ եթե ձեր թվաբանական գիտելիքների շնորհիվ արժեքը բերեք զրոյի, ապա խճճվածքն իրոք կբացվի։ Հրաշալի է։ Քեմբրիջում ունկնդիրները ընտրեցին հետևյալ հաջորդականությունը․

Ոլորելն ու պտտելն այստեղ նշանակված են համապատասխանաբար u→ և r → -ով։

Սա շատ պարզ գաղափարի օրինակ է։ Մենք արդեն գիտեինք թվաբանությունից որոշ  բան, բայց միայն թվերի հետ կապված. և մենք չհասկացանք, որ սա կարող է կիրառվել նաև հանգույցների վրա: Այսպիսով, հանգույցների տեսության այս մասն իրականում մաքուր թվաբանություն է:

Գտնելով այս անսպասելի կապը` եկեք ավարտենք մի փոքր զվարճանալով։ Սկսենք  t = 0-ից և կատարենք պտույտ (նկ. 26):

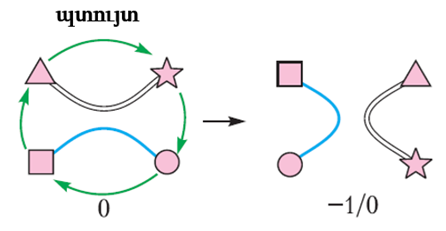
Նկար 26

Ի՞նչ ենք ստանալու։ Հը՞մ։  Մենք ստացանք -1/0 ․ սա ինչ-որ անվերջությո՞ւն է, թե՞ մինուս անսահմանություն: Տեսնենք, թե ինչ կլինի, եթե անսահմանությանը ավելացնենք մեկ : Ինչ-որ բան փոխվո՞ւմ է: Եկեք մի թեքություն անենք (նկ. 27):

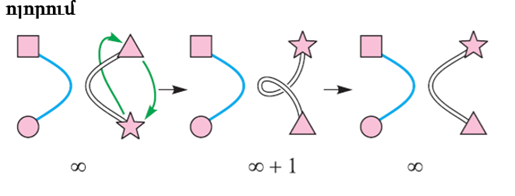
Նկար 27

Հիանալի է։ Մեկը ավելացնում ենք անսահմանությանը, և նորից ստանում ենք անսահմանություն։

Այստեղ մի հզոր գաղափար կա, որը մենք՝ մաթեմատիկոսներս, օգտագործում ենք. դու վերցնում ես այն, ինչ սովորել ես մի տեղ և կիրառում այն ​​մեկ այլ տեղ, որտեղ մաթեմատիկան տեսանելի չէ: Իսկ նա այնտեղ է:

Հեղինակ՝ Ջոն Կոնվեյ

Թարգմանության աղբյուրը՝ այստեղ ։

Թարգմանիչ՝ Մարիամ Համբարձումյան