Թվեր: Թվաբանությունից մինչև բարձրագույն մաթեմատիկա

 
Նախորդ հատվածը

Գլուխ 5. Բաժանում ենք տասնյակների

Խուսափում ենք բաժանման գործողությունից

Շարունակում ենք կոտորակներն ուսումնասիրել: Արդեն պարզեցինք, թե ինչպես կոտորակները բազմապատկենք և բաժանենք ամբողջ թվով: Իսկ ինչպե՞ս կոտորակը կոտորակով բազմապատկենք կամ կոտորակը բաժանենք կոտորակի:

Ենթադրենք, պետք է  1/3 կոտորակը 2 մասի բաժանել: Բոլոր երեք երրորդ մասերը միասին մեկ ամբողջ են կազմում: Եթե այդ մասերից յուրաքանչյուրը կիսենք,  6  մաս կստանանք, որոնք միասին նույնպես 1 են կազմում: Քանի որ այդ փոքր մասերից յուրաքանչյուրը մեկ վեցերորդ մասն է կազմում, կարող ենք պնդել, որ մեկ երրորդի մեկ երկրորդ մասը հավասար է մեկ վեցերորդի: Այդպես դատելով, կարող ենք ցույց տալ, որ մեկ չորրորդի մեկ երկրորդը հավասար է մեկ ութերորդի, իսկ մեկ չորրորդի մեկ երրորդը, համապատասխանաբար, մեկ տասներկուերորդի:

Կոտորակների հետ գործողությունները հարմար է գրառել հետևյալ տեսքով`

Oգտագործում ենք «x» նշանը, քանի որ ճիշտ պատասխանը ստանում ենք հայտարարների բազմապատկումից: Իսկ համարիչնե՞րը: Առաջին հայացքից թվում է, թե համարիչը չի փոխվում, բայց չէ՞ որ 1х1=1:

Որպեսզի այս հարցին պատասխանենք, պետք է պարզենք, թե մեկից տարբեր համարիչ ունեցող  կոտորակների դեպքում ինչպես վարվենք: Դիցուք, պետք է 10-ը բաժանենք հինգ հավասար մասերի: Յուրաքանչյուր մասը կլինի 10-ի մեկ հինգերորդ մասը: Քանի որ 10:5=2, հետևաբար, տասի մեկ հինգերորդ մասը 2-ն է: «Տասի մեկ հինգերորդ» արտահայտությունը գրառվում է 1/5×10։

Այժմ փորձենք այս արտահայտությունը  ներկայացնել կոտարակի տեսքով: Նախ` 1/5-ը կարող ենք ձևափոխել 2/10-ի, եթե կոտորակի համարիչն ու հայտարարը 2-ով բազմապատկենք: Այնուհետ 10-ը կարելի է պատկերել 10/1, համարիչն ու hայտարարը 3-ով բազմապատկել և ստանալ 30/3: 

Այժմ կարող ենք ասել, որ 1/5х10-ը նույն է, ինչ 2/10х30/3: Եթե բազմապատկենք համարիչը համարիչով և հայտարարը հայտարարով, կստանանք 2×30/10×3, այսինքն` 60/30 կամ 2, իսկ դա հենց այն պատասխանն է, որ ակնկալում էինք ստանալ:

Դիտարկենք ուրիշ օրինակ:

Դիցուք, 1/3×1/2  բազմապատկման ժամանակ, փոխարինել ենք 4/12 և 6/12 կոտորակներով՝ համարիչն ու հայտարարը համապատասխանաբար 4-ով և 6-ով բազմապատկելով:

Այժմ ունենք 4/12×6/12  հավասար է 24/144, եթե բազմապատկման ժամանակ «համարիչ х համարիչ», «հայտարար х հայտարար» սխեմայով շարժվենք: Հիմա պատասխանի՝  24/144-ի հայտարարն ու համարիչը բաժանենք 24-ի և կստանանք 1/6, այսինքն` այն պատասխանը, որը ճիշտ ենք համարում 1/3×1/2 բազմապատկման համար:

Նույն կերպ էլ կատարվում է բաժանման գործողությունը: Բաժանելիի համարիչը բաժանում են բաժանարարի համարիչին, իսկ բաժանելիի հայտարարը՝բաժանարարի հայտարարին: 10/21:5/7=(10:5):(21:7) կամ 2/3, բայց այստեղ կարող են բարդություններ ծագել: Ի՞նչ անենք առաջին կամ երկու դեպքում էլ, եթե ամբողջի բաժանելն անհնար է: Այդ դեպքում և´ համարիչը, և´ հայտարարը կարող են կոտորակների տեսքով ներկայանալ, այսինքն կստանանք կոտորակ՝ կոտորակի մեջ:

Բարեբախտաբար, այդպիսի բաժանումից կարելի է խուսափել:  Վերադառնանք մեր նախորդ խնդրին, երբ 10-ը բաժանեցինք 5 հավասար մասերի: Երկու դեպքում էլ ստացանք 2, այսինքն` 10 : 5  և 10х1/2: 5 թիվը կարելի է ներկայացնել 5/1 կոտորակի տեսքով, իսկ այդ կոտորակը կարելի է դիտարկել որպես շուռ տված 1/5:

Այդպիսի կոտորակները, այսինքն` երկու կոտորակները, որոնց առաջինի համարիչը հավասար է երկրորդի հայտարարին, և հակառակը, առաջինի հայտարարը՝ երկրորդի համարիչին, կոչվում են հակադարձ կոտորակներ: Ակնհայտ է, որ 5/1-ը 1/5 կոտորակի շրջվածն է, այսինքն` 5/1 1/5-ը հակադարձ կոտորակներ են, ճիշտ նույն կերպ հակադարձ են համարվում նաև 2/3 և 3/2  55/26 և 26/55 կոտորակները: Այնուհետև, եթե պնդում ենք, որ 10:5 բաժանման ժամանակ ստանում ենք նույն արդյունքը ինչ որ 10х1/2 բազմապատկման դեպքում, նշանակում է, իր հերթին, տրված թվի վրա բաժանումը համարժեք է տրված թվի հակադարձով բազմապատկելուն:

(Ուշադրություն դարձրեք, որ միայն բաժանարարը կարելի է փոխարինել հակադարձ թվով, բաժանելիին սա չի վերաբերում): Արդեն  համոզվել ենք, որ 10/21:5/7=2/3 ։ 

Ենթադրենք, որ բաժանման փոխարեն բազմապատկում ենք հակադարձ կոտորակով 100/21:7/5=70/105: Այժմ այս կոտորակի համարիչն ու հայտարարը բաժանենք 35-ի:
Ստանում ենք 2/3, այսինքն` այն արդյունքը, որը սպասում էինք:

Այժմ կարող ենք բաժանել 5/7-ը 2/3-ի` չվախենալով կոտորակի ներսում կոտորակ ստանալուց, քանի որ բաժանման փոխարեն կատարում ենք հակադարձ կոտորակով բազմապատկում՝ 5/7:2/3=5/7×3/2 և կստանանք 15/14 պատասխանը:

Կոտորակների բազմապատկման ժամանակ պետք է հիշել, որ կոտորակների հերթականությունը նշանակություն չունի: 
Առաջին դեպքում կստանանք  պատասխանը, իսկ երկրորդում՝ և վերջապես, երկու դեպքում էլ կստանանք 70/105 կամ 2/3 (35-ի բաժանելուց հետո): Պետք է նշել, որ երկրորդ տարբերակն ավելի հարմար է: Առաջին դեպքում 10/21 և 7/5 կոտորակները հնարավոր չէ կրճատել, իսկ երկրորդ դեպքում 10/5 և 7/21  կոտորակները կրճատելը հեշտ է:10/5-ը 2/1 է, իսկ 7/21-ը` 1/3, այսպիսով 10/5×7/21 արտահայտությունը վերափոխվեց 2/1×1/3-ի:

Փոքր թվերի հետ աշխատելն ավելի հարմար է, դրա համար էլ, սովորաբար, կոտորակի համարիչն ու հայտարարը բաժանում են միևնույն թվին՝ առանց որևէ տեղափոխություն անելու:

Օրինակ, 7/10×17/49 դեպքում կարելի է մի կոտորակի համարիչն ու մյուս կոտորակի հայտարարը բաժանել նույն թվին` 7-ի: Այդ դեպքում արտահայտությունը  կունենա հետևյալ տեսքը՝ 1/10×17/7:

Այդպիսի օրինակը շատ հեշտ է հաշվել, պատասխանը՝ 17/70, բնականաբար, ինչ եղանակով էլ որ լուծենք, չի փոխվի: Բայց երկրորդ տարբերակը, կոտորակների կրճատմամբ, ավելի հեշտ է: Բազմապատկման ժամանակ կոտորակների «կրճատում» հնարքն այնքան հարմար է, որ  շատ սովորողներ փորձում են այն կիրառել նաև գումարման դեպքում: Սակայն այդ դեպքում հնարքը չի գործում:

7/10+17/49 կոտորակների գումարը բնավ էլ 1/10+17/7 չէ: Առաջին արտահայտության արժեքը հավասար է 513/490, իսկ երկրորդինը` 1239/490:

Դժվարությունն այն է, որ գումարման ժամանակ անհրաժեշտ է կոտորակները միևնույն հայտարարի բերել: Տվյալ դեպքում դա հնարավոր է անել առաջին կոտորակի հայտարարն ու համարիչը բազմապատկելով 49-ով, իսկ երկրորդ կոտորակինը՝  10-ով: Կստանանք 349/490+170/490: Երբ կոտորակները բերեք միևնույն հայտարարի, կրճատումն իր իմաստը կկորցնի, քանի որ կրճատումը կբերի նրան, որ հայտարարները նորից կտարբերվեն, այսինքն գումարումն անհնար կդառնա:

Այնպես որ, խորհուրդ եմ տալիս կոտորակների գումարման դեպքում կրճատման մասին մոռանալ:

Կոտորակները դասավորում ենք  կանոնավոր շարքով

Պետք է ասել, որ կոտորակներով աշխատելը ոչ միշտ է հարմար:

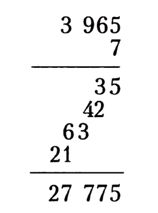Ինչպես էլ գրենք կոտորակը՝  կամ  կամ այն խախտում է թվերի գրառման դիրքային համակարգի կանոնավորությունն ու տրամաբանականությունը: Ասենք, թիվը կարելի է գրել` օգտագործելով դիրքային արժեքները: Դա երեք հազարյակ գումարած մեկ հարյուրյակ գումարած չորս տասնյակ գումարած երեք միավոր և գումարած երեք քառորդն է: Քանի դեռ չէինք հասել այդ չարաբաստիկ կոտորակին, ամեն ինչ տրամաբանական էր: Շարժվելով ձախից աջ` յուրաքանչյուր հաջորդ  դիրքը հավասար է նախորդի մեկ տասներորդին:  

Այլ կերպ ասած, 1000х1/10=100; 100х1/10=10; 10х1/10=1:

Ամեն ինչ հիանալի է, բայց ինչո՞ւ պետք է կանգ առնել միավորի վրա: Ինչո՞ւ այդ շարքը չշարունակենք դեպի  աջ՝ մեկից փոքր տիրույթը: Այն կունենա հետևյալ տեսքը. 1х1/10=,1/10×1/10=1/100, 1/100×1/10=1/1000 և այլն: Այսպիսով, եթե դիրքային շարքը շարունակենք միավորից փոքր թվային տիրույթ, կստանանք տասնորդական, հարյուրերոդական, հազարերորդական և այլն: 

Այժմ դիտարկենք 1/2 կոտորակը: Եթե հայտարարն ու համարիչը բազմապատկենք միևնույն թվով, տվյալ դեպքում 5-ով, կոտորակի մեծությունը դրանից չի փոխվի: Արդյունքում կստանանք՝ 1/2⁼5/10: Նշանակում է, որ թիվը կարելի է ներկայացնել տեսքով, կամ 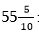 կամ 55,5, կամ հիսունհինգ ամբողջ հինգ տասներորդ: Նորից դիրքային թիվ ստացանք, բայց այժմ ամբողջից ստորակետով առանձնացված կոտորակային մաս ունենք: 

55,5 թիվը դիրքային է, և այն կարելի է կարդալ ինչպես հինգ տասնյակ գումարած հինգ միավոր գումարած հինգ տասներորդ:

Մի կոտորակ ևս դիտարկենք՝ 3/4: Եթե համարիչն ու հայտարարը բազմապատկենք միևնույն թվով, տվյալ դեպքում արդեն 25-ով, այս դեպքում ևս կոտորակի արժեքը չի փոխվի:  Արդյունքում կստանանք 3/4=75/100 կամ 70/100+5/100 կամ 7/10+5/100: Նշանակում է, որ 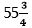թիվը, կարելի է ներկայացնել  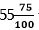տեսքով, կամ 55,75, կամ հիսունհինգ ամբողջ և յոթանասունհինգ հարյուրերորդ: Նորից դիրքային թիվ ստացանք և  ամբողջից ստորակետով առանձնացված, կոտորակային մաս ունենք: 55,75 թիվը դիրքային է, և այն կարելի է կարդալ որպես հինգ տասնյակ գումարած հինգ միավոր գումարած յոթանասուն հարյուրերոդ գումարած հինգ հարյուրերորդ: Որոշակի քանակով տասնորդական, կամ հարյուրերոդական, կամ հազարերոդական և այլն, այսինքն` դիրքային թվի տեսքով ներկայացված կոտորակներն անվանում են տասնորդական: Ամբողջ մասը կոտորակային մասից առանձնացնող ստորակետն անվանում են տասնորդական ստորակետ: Միավորից փոքր տասնորդական կոտորակը կարելի է գրել 7 տեսքով: Սակայն գործողությունների կատարման ընթացքում ստորակետի նշանը կորցնելու իրական վտանգ կա, որն էլ կոտորակը կվերածի ամբողջ թվի: Դրա համար էլ գրառման հետևյալ ձևն են ընտրել, երբ բացակայող ամբողջը փոխարինում են զրոյով և կոտորակը   ստանում է 0,7 տեսք (այսինքն` զրո միավոր գումարած յոթ տասներորդ, սակայն կարելի է ասել ուղղակի յոթ տասներորդ):

Բացի դրանից, 7/10 կարելի է գրել ինչպես 0,70, կամ 0,700, կամ 0,7000, կամ 0,700000000000: Տասնորդական կոտորակների վերջին նշանակալի թվանշանից հետո հարյուրերորդ, հազարերորդ, տասհազարերորդ և այլն նիշեր ավելացնելով, նրա արժեքը չի փոխում:

Տասնորդական կոտորակի հիմնական առավելությունն այն է, որ կարելի է գումարում ու հանում կատարել`չմտածելով կոտորակային մասի մասին և կոտորակային թվի հետ վարվել` ինչպես ամբողջի հետ: Կարելի է նաև համրիչից օգտվել: Դրա համար միավորների շարքը պետք է տեղադրել համրիչի մեջտեղում, վերևում տասնյակների, հարյուրյակների, հազարյակների և այլն շարքերն են, իսկ ներքևում` տասնորդականների, հարյուրերորդականների, հազարերորդականների և այլն: 

Այդպիսի համրիչների վրա կարելի է գումարել և հանել և՛ հարյուրյակներ, և՛ հարյուրերոդականներ, և՛ հազարյակներ, և՛ հազարերորդականներ և այլն:

Նույն կանոնները ճիշտ են նաև թղթի վրա հաշվարկներ կատարելիս: Ենթադրենք, պետք է գումարել 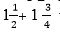արտահայտությունը՝ պահպանելով սովորական կոտորակների տեսքով: Սկզբում պետք է կոտորակները 3/2+7/4 տեսքով ներկայացնել, հետո ընդհանուր հայտարարի բերել 6/4+7/4, որն էլ հավասար է 13/4, կամ 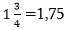: Իսկ հիմա տասնորդական կոտորակներով գումարում կատարենք:  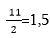 , իսկ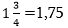 

Գումարումը սյունակով կատարենք.

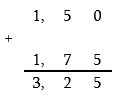
Ուշադրություն դարձրեք, որ 1,5 թիվը գրել ենք 1,50 տեսքով, որովհետև երկրորդ թիվը հարյուրերորդականի կարգում թվանշան ունի: Եթե այդպես չանենք, ապա սխալ գրառելու պատճառով սխալվելու վտանգ կա.

Տասնորդական կոտորակներով ստացանք 3,25 պատասխանը, կամ 3 գումարած 2/10  գումարած 5/100: Եթե գումարում կատարենք, կստանանք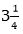, այսինքն` այն պատասխանը, որը ճիշտ ենք ընդունում:

Գործնականում տասնորդական կոտորակներից սովորական կոտորակներին անցնելու անհրաժեշտություն չկա: Մեկ անգամ տասնորդական կոտորակների հետ գործողությունները յուրացնելով` կկարողանանք նրանց օգնությամբ բոլոր հաշվարկներն արագ և համեմատաբար հեշտ կատարել:

Ամերիկյան առողջ բանականություն և ամերիկյան անհեթեթություն

Ամերիկյան դրամային համակարգը տասնորդական համակարգի հարմարավետության և արդյունավետության օրինակ է: Այն իր բնույթով տասական է: Դիտարկենք այն՝ սկսելով ամենամանր, վաղուց գործածությունից դուրս եկած, դրամներից:

10 միլը հավասար է 1 ցենտի, 10 ցենտը հավասար է 1 դայմի, 10 դայմը հավասար է 1 դոլարի, 10 դոլարը հավասար է 1 իգլի։ (Իրականում ոչ միլը, ոչ իգլը գործնականում չեն օգտագործվում, սակայն մեզ համար կարևորը սկզբունքն է): Իգլ (կամ արծիվ) անվանում էին 10 դոլարի համարժեք ոսկե դրամը, որը հատել են Միացյալ Նահանգներում: Դրամն անվանումը ստացել է երկրի խորհրրդանիշ արծվից, որը պատկերված է հակառակ կողմում: Մեծ Բրիտանիայում ոսկե դրամը սովերեն էին անվանում, քանի որ նրա վրա պատկերված էր միապետի, սուվերենի նկարը: Հիմա ոսկե դրամները շրջանառությունից դուրս են եկել, և իգլ և սովերեն անունները նույնպես մոռացվում են: Իսկ առաջներում շրջանառվում էին ոչ միայն իգլները, այլև կրկնակի իգլները (20 դոլար ոսկով), կես իգլներն (5 դոլար ոսկով) ու քառորդ իգլները (2,5 դոլար ոսկով):

Տասական համակարգը տարածվում է խոշոր նաև գումարների վրա: Այսպես, С նոութ միավորը 100 դոլարն է, իսկ գրանդը` 1000 դոլարը:

Այսպիսի համակարգի շնորհիվ ցանկացած դրամական գումար միշտ կարելի է գրառել տասնորդական կոտորակների տեսքով: Եթե ձեր գրպանում 13,26 դոլար է, նշանակում է դուք ունեք 1 տասդոլարանոց, 3 հատ մեկդոլարանոց թղթադրամ, 2 տասնորդական դոլար, այսինքն` 2 դայմ և 6 հարյուրերորդական դոլար, այսինքն` 6 ցենտ:

Բայց հնարավոր է, ձեզ մոտ ուրիշ թղթադրամներ և մանրադրամներ լինեն:

Օրինակ, 1 հինգդոլարանց թղթադրամ, 1 երկուդոլարանոց թղթադրամ, 1 մեկդոլարանոց թղթադրամ, 5 կեսդոլարանոց, 9 քառորդ դոլար մանրադրամ, 4 դայմ, 2 նիկել և 1 պեննի: Սակայն այս բոլոր տարօրինակ մանրադրամների անվանական գները միշտ գրառվում են տասնորդական կոտորակների տեսքով: Կեսդոլարը երբեք չի գրվում $1/2 տեսքով, այլ այսպես՝ $0,5: Քառորդ դոլարը միշտ գրվում է $0,25 տեսքով, դայմը՝ $0,10 , նիկելը՝ $0,05 և վերջապես պեննին՝ $0,01: (Անվանական գները կարելի է գրառել ոչ թե դոլարով, այլ ցենտով, բայց միևնույն է, այս դեպքում էլ է տասական համակարգը պահպանվում)։

Մենք դրամական գործարքներում այնպես ենք հարմարվել տասական համակարգի հարմարավետությանը, որ արդեն այդ մասին չենք էլ մտածում: Սակայն այդպիսի համակարգը ոչ միշտ է գոյություն ունեցել: Հին բրիտանական դրամական համակարգը հիմնված էր այլ սկզբունքների վրա: Ամենամանր մետաղադրամը ֆարտինգն էր, 4 ֆարտինգը 1 պեննի էր, 12 պենսը` 1 շիլլինգ, իսկ 20 շիլլինգը՝1 ֆունտ. Անգլիացիների համար հեշտ չէր դրամական հաշվարկներով զբաղվելը: Ինչպե՞ս գումարեն 4 ֆունտ, 8 շիլլինգ, 2 պենս ու 15 ֆունտ, 19 շիլլինգ ու 11 պենսը: (Պատասխանը 20 ֆունտ, 8 շիլլինգ, 1 պեննի է, բայց չեմ պատրաստվում բացատրել, թե ինչպես հաշվեցի այդ գումարը): Ժամանակին բրիտանացի դպրոցականները ստիպված էին շատ ժամանակ ծախսել որպեսզի դրամական միավորների հետ գործողություններ կատարել սովորեին: Միևնույն ժամանակ ամերիկացի դպրոցականները առաջին մետաղադրամներով հեշտությամբ թվաբանություն սովորել սկսեցին:

Չնայած Ամերիկայում էլ բավական անհեթեթ չափման միավորներ կան, ճիշտ է, ոչ դրամական, այլ երկարության, զանգվածի և ծավալի: Միացյալ նահանգներից և էլի մի քանի պետություններից բացի, աշխարհի շատ երկրներում արդեն վաղուց են անցել 1791 թվականին Ֆրանսիայում ընդունված չափման և զանգվածի մետրային համակարգի:

Մետրային համակարգը տասական է: Օրինակի համար դիտարկենք երկարության միավորները: Մետրային համակարգում երկարության հիմնական միավորը մետրն է (որը հավասար է 39,37 դյույմի): Համակարգի անվանումը հենց այդ միավորից է ստացել իր անվանումը: («Մետր» բառը փոխանցվել է լատիներենից (metrum), որտեղ այն «չափել» է նշանակում): Տարբեր երկարության միավորների նախածանցները, որոնց մասին ստորև կպատմեմ, նույնպես լատիներենից և հուներենից են փոխանցվել:

Հունական նախածանցներն օգտագործում են մետրից մեծ միավորները նշանակելու համար (դեկա-տասը, հեկտո-հարյուր և կիլո-հազար), իսկ լատիներենը՝ փոքր միավորների համար (դեցի, սանտի և միլի, համապատասխանաբար տասը, հարյուր և հազար):

Տասը մետրը կազմում է դեկամետր, տասը դեկամետրը՝ մեկ հեկտոմետր, իսկ տասը հեկտոմետրը՝ մեկ կիլոմետր: Կարելի է փոքրացնելու ուղղությմաբ գնալ: Մետրի մեկ տասներորդ մասը դեցիմետրն է, դեցիմետրի մեկ տասներորդը մեկ սանտիմետրն է, իսկ սանտիմետրի մեկ տասներորդը՝ մեկ միլիմետրը:

Նշանակում է, որ եթե ինչ-որ հեռավորություն հավասար է 2 կիլոմետր, 5 հեկտոմետր, 1 դեկամետր, 7 մետր, 8 դեցիմետր, 2 սանտիմետր և 9 միլիմետր, ապա հեռավորությունը հավասար է 2517,829 մետրի: Այսպիսի չափումներով հեշտ է ցանկացած հաշվում կատարելը: Ասենք, եթե ունեք երկու պատկեր, մեկը` 2 մետր, 8 դեցիմետր և 9 սանտիմետր երկարությամբ, իսկ մյուսը` 5 մետր, 5 դեցիմետր և 5 սանտիմետր երկարությամբ, ապա երկու պատկերների ընդհանուր երկարությունը կազմում է 2,89+5,55 կամ 8,44 մետր, որն էլ նույնն է թե` 8 մետր, 4 դեցիմետր և 4 սանտիմետրը:

Իսկ հիմա եկեք համեմատենք այս համակարգը երկարության չափման անգլիական և ամերիկյան համակարգի հետ: Այս համակարգի հիմնական միավորը դյույմն է: 12 դյույմը 1 ֆութ է: 3 ֆութը 1յարդ է: 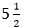յարդը՝ մեկ ռոդ է, 40 ռոդը՝ 1 ֆերլոնգ, իսկ 8 ֆերլոնգը՝ 1 մղոն: Բնականաբար, սա շատ դժվար է, և´ ռոդները, և´ ֆիլոնգները մեր օրերում գործնականում չեն կիրառում: Ընդունված է, որ 1760 յարդը (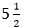х40х8) 1 մղոն է: Այժմ փորձենք հաշվել, թե ինչի է հավասար 1 մղոն 1632 յարդին գումարած 2 մղոն և 854 յարդ: Պատասխանը 4 մղոն և 762 յարդ է: Հետաքրքիր է, կգուշակե՞ք, թե ինչպես եմ այդ գումարը ստացել և կկարողանա՞ք կրկնել իմ հաշվարկները:

Այժմ անցնենք ավելի մանր միավորների: Փորձենք գումարել 3 յարդ 2 ֆութ 8 դյույմը և 5 յարդ 2 ֆութ 7 դյույմը: Պատասխանը 9 յարդ 2 ֆուտ և 3 դյույմ է: Ինչպե՞ս հաշվեցի:

Ամերիկացի դպրոցականներն այդ բազմազան չափման միավորներից գլուխ հանելու համար ստիպված են զգալի ժամանակ ծախսել:

Սակայն բացի երկարության միավորից, կան նաև ծավալի, զանգվածի, մակերեսի միավորները, և նրանցից յուրաքանչյուրը ներառում է բազմաթիվ բարդ և անիմաստ տարրեր: Բնականաբար, դպրոցականները երբեք էլ այդ բոլոր միավորները և նրանց միջև հարաբերությունները չգիտեն:

Ռուսաստանում երեխաների համար ավելի հեշտ է: Մեզ մոտ մետրային համակարգն է ընդունված, որը այդքան գլխացավանք չի պատճառում:
Ինչո՞ւ Միացյալ Նահանգներում և Մեծ Բրիտանիայում հարմարավետ չափման մետրային համակարգին չեն անցնում: Առաջին հերթին, մեր օրերում դա էական ներդրումներ է պահանջում, քանի որ բոլոր հաստոցները, գործիքներն ու նախագծման համակարգը պետք է նոր չափման համակարգի տեղափոխեն: Բայց հիմնական խոչընդոտը ավանդույթին նվիրվածությունն է: Մարդիկ դժկամությամբ են հրաժարվում սովորույթներից, և որպեսզի նրանք նոր համակարգին հակվեն, կառավարության հարկադրական գործողություններ կպահանջվեն: Իսկ բրիտանացիներն ու ամերիացիները պարտադրանքի սովոր չեն: Սա նույնպես ավանդույթ է:

Միևնույն ժամանակ և՛ բրիտանացի, և՛ ամերիկացի գիտնականները վաղուց են անցել մետրային համակարգի: Ընդ որում, Ամերիկայում այն երբեմն օգտագործում են ամենաանսպասելի ձևով: Օրինակ, երբ տնտեսագետներն ու բանկային աշխատողները պետք է մեծ գումարների հետ հաշվարկներ կատարեն, կատակով ասում են «կիլոբաքս» («բաքս» բառը դոլար է նշանակում, խոսակցական լեզու է եկել պոկեր խաղացողների ժարգոնից): Միլիոն բաքսը նմանակերպ անվանում են «մեգաբաքս»:
(«Մեգա» հուներեն նշանակում է «մեծ», իսկ մետրային համակարգում՝ միլիոն):

Տասնորդական ստորակետի դիրքի որոշումը

Կարծում եմ, կհամաձայնեք, որ տասնորդական համակարգը դրախտ է երկրի վրա, հատկապես, եթե այն համեմատենք սովորական կոտորակների համակարգի հետ: Սակայն, ինչպես երկրի վրա ցանկացած դրախտ իր հակառակ կողմն ունի, այնպես էլ տասնորդական կոտորակների համակարգն ունի իր թերությունները:

Օրինակ, անհրաժեշտ է շատ ուշադիր հետևել տասնորդական ստորակետի դիրքին: Դիտարկենք 0,2х0,2 բազմապատկման օրինակը: Կարող եք փորձել այս օրինակը գումարման նմանությամբ լուծել 2+2=4, նաև՝ 2×2=4, ապա 0,2+0,2= 0,4։ Հնարավո՞ր է, 0,2х0,2=0,4 :
Ոչ, հնարավոր չէ, հիմա դա կապացուցեմ: Վերադառնանք սովորական կոտորակներին, որոնց հետ այնքան լավ վարվել սովորեցինք 0,2=2/10:

Այժմ կոտորակները հին եղանակով բազմապատկենք. 2/10×2/10=4/100 (համարիչը՝ համարիչով, հայտարարը՝ հայտարարով): Իսկ 4/100-ը տասնորդական կոտորակով 0,04-ն է:

Հետևաբար, 0,2х0,2 ամենևին հավասար չէ 0,4-ի: 0,2х0,2=0,04 :

Կարող ենք տասնորդական կոտորակների բազմապատկման ևս մի քանի օրինակ լուծել, փոխարինելով սովորական կոտորակների համարժեքով: Օրինակ` 0,82х0,21=0,1772, իսկ 0,82х2,1=1,772: (Կարելի է ստուգել հետևյալ ձևով. 82/100×21/100=1722/10000, իսկ 82/100×21/10=1722/1000):

Հիմա կարող ենք ընդհանուր կանոնը ձևակերպել. տասնորդական կոտորակների բազմապատկման ժամանակ արտադրյալում տասնորդական ստորակետից աջ գտնվող թվանշանների քանակը հավասար է արտադրիչների տասնորդական ստորակետից աջ գտնվող թվանշանների ընդհանուր քանակին: Այսպես, 0,2х0,2 արտադրյալում, արտադրիչների մեջ ստորակետից աջ գտնվող թվանշանների ընդհանուր քանակը հավասար է 2-ի, նշանակում է, որ 0,2х0,2=0,04 (տասնորդական ստորակետից աջ գտնվող զրոն նույնպես նշանակալի թվանշան է):

Բնական է, եթե արտադրիչներից մեկը ամբողջ թիվ է, ապա այն չի ազդում տասնորդական ստորակետի դիրքի վրա: Տասնորդական ստորակետի դիրքը կլինի այնպիսին, ինչպիսին, տասնորդական արտադրիչինն է:

Այսինքն, 0,2х2=0,4; 1,5х5=7,5, իսկ 1,1х154=169,4:

Այս արդյունքները համապատասխանում են բազմապատկման կանոնին, և ցանկացած դեպքում պատասխանի մեջ տասնորդական ստորակետից աջ գտնվող թվանշանների քանակը հավասար է արտադրիչների տասնորդական ստորակետից դեպի աջ գտնվող թվանշանների ընդհանուր քանակին:

Բաժանման դեպքում տասնորդական ստորակետի դիրքը կարելի է համանման մեթոդիկայով որոշել՝ գործելով հակառակ կարգով: Բայց, սովորաբար, բաժանման ժամանակ փորձում են ընթացքը հեշտացնել և համարիչն ու հայտարարը (եթե բաժանումը կատարում են սովորական կոտորակների օգնությամբ) բերում են ամբողջ՝ ստորակետից հետո նշանակալի թիվ չպարունակող, թվի տեսքի:

Ենթադրենք, 1,82-ը պետք է բաժանել 0,2-ի: Այս արտահայտությունը կարելի է գրառել այսպես 1,82/0,2:

Չփոխելով կոտորակի արժեքը` համարիչն ու հայտարարը բազմապատկում է 10-ով: Այդ դեպքում 1.82×10 (տասնորդական ստորակետի դիրքորոշման կանոնին համապատասխան) հավասար է 18,20, կամ 18,2, քանի որ նշանակալի թվից աջ գտնվող զրոն թվի արժեքը չի փոխում, և հետևաբար, այն կարելի է չգրել:

Ճիշտ այդպես էլ 0,2х0=2,0 կամ ուղղակի 2 (քանի որ 2 գումարած զրո տասնորդական հավասար է 2):

Հետևաբար, կոտորակը կարելի է գրառել ինչպես 18,2/2, և այժմ հայտարարը ամբողջ թիվ է, հետևաբար, բաժանման ընթացքում տասնորդական ստորակետի դիրքը չի փոխվում, այնպես, ինչպես բաժանման ժամանակ:

Քանի որ համարիչում ստորակետից հետո մեկ նշանակալի թվանշան է, ապա արդյունքում, ստորակետից աջ, պետք է մեկ նշանակալի թվանշան լինի, այսինքն` 18,2/2=9,1:

Տասնորդական կոտորակների բաժանումը յուրացնելով` կարող ենք սովորական կոտորակները վերափոխել տասնորդականի:

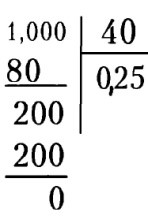Ենթադրենք, ուզում ենք 1/40–ի տասնորդական համարժեքը գտնել: Կարող ենք այս կոտորակը ներկայացնել 1,0000/40 տեսքով և հետո բաժանումը կատարել: Քանի որ ամբողջ թվի ենք բաժանում, ապա տասնորդական ստորակետի դիրքը չի փոխվում: Կատարենք բաժանումը (տես նկարը)։

Այսպիսով, ցույց տվեցինք, որ 1/40-ի տասնորդական համարժեքը հավասար է 0,025-ի: Կարելի է ստուգել` 0,025-ը վերափոխելով սովորական կոտորակի:

 0,025=2/100+5/1000, կամ 20/1000+5/1000 կամ 25/1000, կամ եթե բաժանում կատարենք, ապա՝ 1/40, ինչպես ենթադրում էինք:

Տեղափոխում ենք տասնորդական ստորակետը

Վերադառնանք 10-ով բազմապատկելու օրինակներին: Նախորդ հատվածում 10-ով բազմապատկեցինք 1,82-ը և ստացանք 18,2: Ուշադրություն դարձրեք, որ 10-ով բազմապատկելը իրականում համընկնում է տասնորդական ստորակետը մեկ կարգ աջ տեղափոխելուն: Ճիշտ այդպես էլ 100-ով բազմապատկելը հանգում է տասնորդական ստորակետը երկու կարգ աջ տեղափոխելուն, իսկ 1000-ով բազմապատկելը՝ համապատասխանաբար, երեք միավոր: Դրանում կարող եք ինքներդ հեշտությամբ համոզվել:

10-ի վրա բաժանումը հագեցվում է բազմապատկման հակառակ գործողությանը, տվյալ դեպքում տասնորդական զտորակետը մեկ կարգ դեպի ձախ տեղափոխելուն, 100-ի վրա բաժանումը՝ երկու միավոր դեպի ձախ, իսկ 1000-ի վրա բաժանումը՝ համապատասխանաբար, երեք միավոր դեպի ձախ: Քանի որ 1,82:10, հակադարձ կոտորակների կանոնի համաձայն, հավասար է 1,82х0,1, որն էլ իր հերթին հավասար է 0,182: Այսպիսի պատասխան կստանայինք, եթե տասնորդական ստորակետի տեղափոխման կանոնի համաձայն ստորակետը մեկ կարգ ձախ տեղաշարժենք: Քանի որ 10-ով բազմապատկելը կամ 10 –ի վրա բաժանելը կատարում են ուղղակի տասնորդական ստորակետը տեղափոխելով աջ կամ ձախ, հարմար է տոկոսներին անցնել: Վաղուց սովորություն է դարձել, որ մարդիկ կամ կազմակերպությունները, որոնք պարտքով դրամ են տալիս, բացի իրենց տրամադրած գումարից, պարտք տրամադրելու համար, որոշակի ավել գումար են ետ ստանում: Այդ գումարը ստացել է «տոկոս» անունը:

Այդ գումարը փոխհատուցում է այն բանին, որ պարտատերը ինչ որ ժամանակ մնում է առանց իր գումարի, բացի այդ այն գումարը ետ չստանալու ռիսկի փոխհատուցում է: Օրինակ, մասնավոր անձը կամ կազմակերպությունը կարող է յուրաքանչյուր 100 դոլար պարտքի համար տարեկան 6 դոլար տոկոս ուզել:

Քանի որ շատ հաճախ այդ «տոկոսները» հաշվարկվում են յուրաքանչյուր 100 դոլարի հաշվարկով («տոկոս» բառը մեզ է հասել լատիներենից, որտեղ «per cent» նշանակում է «հարյուրի»):

Սովորաբար եկամուտների, հավելագների և միջնորդավճարների, ինչպես նաև շատ ուրիշ ցուցանիշների հաշվարկների ժամանակ օգտագործում են տոկոսը:

Փաստորեն մեկ տոկոսը յուրաքանչյուր 100-ի դիմաց 1 դոլարն է, այսինքն` 1/100:

Որպեսզի ցանկացած թվի մեկ տոկոսը գտնենք, պետք է տասնորդական ստորակետը երկու կարգ դեպի ձախ տեղափոխենք: Այսպես, 1350 դոլարի 1 տոկոսը հավասար է 13,50 դոլարի:

1350–ի 6 տոկոսը կազմող գումարը, պետք է լինի 6х1/100х1350=6х13,50, կամ 81,00 :

Տասը տոկոս միջնորդավճարը կազմում է թվի 10/100 մասը, այսինքն՝ 1/10:

Այս դեպքում տասնորդական ստորակետը մեկ կարգ ձախ է տեղափոխվում: Իսկ 10 տոկոս միջնորդավճարը կազմում է 135 դոլար:

Երբեմն տոկոսները հաշվելիս որոշ խնդիրներ են առաջանում: Օրինակ, 675,37 դոլար գումարի 1 տոկոս միջնորդավճարը կազմում է 6,7537 դոլար: Գործնական նպատակներով տասնորդական ստորակետից հետո երկու նիշից ավելի պետք չէ, և մնացած թվանշանները կլորացվում են: Կլորացնելուց հետո միջնորդավճարը կլինի 6,75 դոլար: Այս բոլոր առնչությունները լավ են աշխատում դրամական տասական համակարգում: Հին բրիտանական դրամական համակարգում տոկոսային հաշվարկներն այնքան էլ հարմար չեն: Այնքան էլ հեշտ չէ 135 ֆունտ 10 շիլինգի10 տոկոսը գտնել: Իմ հաշվարկով 13 ֆունտ 11 շիլինգ կանի, դուք էլ փորձեք հաշվել:

Անվերջ տասնորդական կոտորակներ

Տասական համակարգում, բացի տասնորդական նշանի դիրքորոշումից, շատ ավելի լուրջ խնդիրներ են առաջանում: Բանն այն է, որ մի շարք կոտորակներ հնարավոր չէ ներկայացնել սովորական տասնորդական համարժեքի տեսքով:

Դիտարկենք, օրինակ 1/3-ը: Փորձենք այն տասնորդական կոտորակի տեսքով ներկայացնել: Համապատասխան տասնորդական կոտորակը գտնելու, պետք է 1/3-ը  գրենք 1,0000000/3 տեսքով, բաժանումը հետևյալ եղանակով կատարենք.

Բաժանումը շարունակելու իմաստը չկա, արդեն համոզվեցիք, որ այն կարելի է անվերջ շարունակել: 1/3-ի տասնորդական համարժեքը 0,3333333333… և այլն է:

Որպես հաջորդ օրինակ դիտարկենք 1/7 կոտորակը:

Ներկայացնենք այն 1,0000000/7 տեսքով և բաժանումը կատարենք: (Այս գործողությունը լիովին վստահում եմ ընթերցողին:) Ստանում ենք հետևյալ տասնորդական համարժեքը` 1/7=0,142857142857142857142857… և այլն: Ձեր ուշադրությունն եմ հրավիրում, որ 1/7–ի տասնորդական համարժեքը անվերջ պարբերական տասնորդական կոտորակ է: Տասնորդական համարժեքը անվերջ կոտորակ է ինչպես 1/3-ի, այնպես էլ 1/7-ի դեպքում, սակայն 1/3-ի դեպքում ունենք 3 թվանշանի անվերջ կրկնություն, իսկ 1/7- դեպքում՝ 142857 թվանշանների հաջորդականության կրկնություն: Սրանք պարբերական տասնորդական կոտորակների օրինակներ են:

Ըստ էության, բոլոր տասնորդական կոտորակները կարելի է դիտարկել որպես անվերջ պարբերական, քանի որ ցանկացած տասնորդական կոտորակի վերջում կարելի է անվերջ քանակով զրոներ ավելացնել, դրանից թվի արժեքը չի փոխվում:

Օրինակ` ½-ի տասնորդական համարժեքը 0,5 է: Այդ թիվը կարելի է ներկայացնել 0,5000000000000 տեսքով՝ անվերջ կրկնվող զրոներով: Երբեմն պարբերական տասնորդական կոտորակում անվերջ կրկնվող թվանշանները, վերևում դրված կետով են նշանակում: Այսպես, 1/3-ը կարելի է ներկայացնել 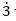տեսքով, իսկ ½-ը՝ :

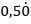Եթե պարբերական կրկնվողը թվերի խումբ է, դրանք վերցնում են փակագծերի մեջ և կետը դնում թվանշաններից մեկի վրա: Այսպես,  :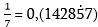

Իսկապես, ցանկացած կոտորակ կարելի է ներկայացնել համարժեք անվերջ պարբերական կոտորակի տեսքով (նունիսկ եթե այդ անվերջ կրկնվող թվանշանը 0-ն է), և, հակառակը, ցանկացած անվերջ պարբերական կոտորակ կարող ենք ներկայացնել ոչ տասնորդական վերջավոր կոտորակի, այսինքն` ամբողջ թվերի հարաբերության տեսքով: Ձեզ մոտ, իհարկե, հարց առաջացավ, թե ինչպես թվաբանական գործողություններ կատարենք պարբերական տասնորդական կոտորակներով: Կարելի է, օրինակ, օգտագործել ոչ տասնորդական համարժեքը, ասենք 0,333333..-ի փոխարեն օգտագործել 1/3: Սակայն, ինչքան էլ տարօրինակ է, գիտական և ինժեներական բարդ խնդիրներում, անվերջ պարբերական տասնորդական կոտորակները դժվարություններ չեն առաջացնում: Բայց կան գործողություններ կատարելիս դժվար, և լուրջ խնդիրներ լուծելիս անհարժեշտ թվեր, որոնց մասին կպատմեմ հաջորդ գլուխներում: 

Շարունակությունը

Թարգմանություն ռուսերենից
Թարգմանիչ՝ Մանուշակ Աբրահամյան