Ս․ Դվորյանինով, Ա․ Նասիպով
Թարգմանիչ՝ Լիանա Հակոբյան
Հայտնի է, որ առաջին հայացքից բոլորովին տարբեր թվացող խնդիրները ըստ էության նույնն են։ Օրինակ`
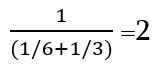
Այս կոտորակի արժեքը կարող է լինել որպես երկու տրակտորիստների համատեղ աշխատանքի խնդրի պատասխանը, որոնցից մեկը դաշտը հերկում է 6 ժամում, իսկ մյուսը՝ 3 ժամում։
Նմանատիպ խնդրում պետք է գտնել AB ճանապարհով իրար ընդառաջ շարժվող երկու գնացքների հանդիպման ժամանակը։
Ըստ պայմանի մի գնացքը ամբողջ ճանապարհը անցնում է 6 ժամում, իսկ մյուսը՝ 3 ժամում։ Այս խնդրում ևս կա համատեղ աշխատանք։
Այն կատարել, նշանակում է անցնել AB ճանապարհը։
Կարելի է ասել՝ հետք թողնել ճանապարհին։
Մեր հոդվածի կենտրոնում երկու նմանատիպ խնդիրներ են, որոնց նմանությունը միշտ չէ, որ ակնհայտ է։
Առաջադրանք 1․ A նավամատույցից գետի հոսանքի ուղղությամբ շարժվեց շոգենավը։ Նրա դիմաց՝ A նավամատույցից 50կմ հեռավորության վրա էր գտնվում լաստը։ Շոգենավը և լաստը B նավամատույց հասան միաժամանակ։ Հաջորդ օրը A նավամատույցից գետի հոսանքի ուղղությամբ շարժվեց նավակը, որի արագությունը երեք անգամ մեծ էր շոգենավի արագությունից։ Նրա առջև՝ A-ից 75 կմ հեռավորության վրա էր գտնվում մեկ ուրիշ լաստ:
Այս դեպքում ևս նավակը և լաստը հասան B նավամատույց միաժամանակ։
Գտե՛ք A և B նավամատույցների միջև հեռավորությունը։
Նկար 1-ում նշված են շոգենավի և նավակի սեփական արագությունները՝ համապատասխանաբար v и 3v, իսկ գետի արագությունը՝ vр։
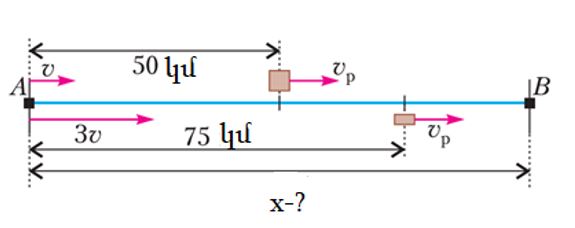
Հավասարեցնելով առաջին դեպքում լաստի և շոգենավի անցած ժամանակները, իսկ երկրորդ դեպքում՝ լաստի և նավակի ժամանակները՝ կստանանք երկու հավասարումների համակարգ.
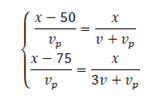
Այստեղից էլ կատարելով պարզ ձևափոխություններ՝ կստանանք․
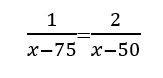
x=100։
Նշանակում է A և B նավամատույցների միջև հեռավորությունը 100կմ է։
Կազմելով հավասարումները՝ կարելի է ասել, որ շոգենավի, նավակի և երկու լաստերի շարժումը դիտարկեցինք գետի ափից։ Լուծենք այս խնդիրը այլ ճանապարհով։
Այժմ պատկերացնենք, որ մենք այդ նավերի նավապետերն ենք։
Շոգենավի նավապետը տեսնում է կամ գիտի, որ իր դիմաց՝ 50 կմ հեռավորության վրա է գտնվում լաստը և, որ շոգենավը մոտենում է լաստին v արագությամբ։
Ենթադրենք շոգենավը հասնում է լաստին t ժամանակում։
v արագությամբ 75կմ ճանապարհը հաղթահարելու համար պարզ է, որ նրանից կպահանջվի 1,5 անգամ շատ ժամանակ, այսինքն՝ 1, 5t ։
Բայց նավակը մոտենում է լաստին 3v արագությամբ, հետևաբար նավակը կհասնի լաստին 0,5 t ժամանակում։
Այժմ հասկանանք, թե ինչ է նշանակում այս ամենը երկու լաստերի համար։
Նշանակում է, որ առաջին լաստի հեռավորությունը B նավամատույցից երկու անգամ ավելի երկար է երկրորդ լաստի՝ B նավամատույցի հեռավորությունից, այսինքն՝ x-50=2(x-75)
Նորից ստանում ենք՝ x=100:
Երկրորդ լուծումը (թվաբանական) շատ ավելի տպավորիչ է երևում։
Սակայն այս լուծումը պահանջում է որոշակի մտավոր ջանք և փորձ՝ ուղիղ և հակադարձ համեմատական մեծությունների միջև եղած կախվածությունը կիրառելու։
Առաջին լուծումը շարժման խնդիրների վերաբերյալ ստանդարտ մոտեցումն է, երբ մեկը գնում է մյուսի ետևից և հասնում է նրան, կամ գնում են իրար ընդառաջ։
Այս (հանրահաշվական) լուծումը որևէ ստեղծագործական միտք չի պահանջում, այստեղ հավասարումներն են մեր փոխարեն մտածում։
Ի դեպ, շեղ գրված բառերը որպես հոդվածի վերնագիր երկու անգամ հրապարակված են եղել «Քվանտ» ամսագրում (կարող եք տեսնել №9, հրապարակված 1981թ․-ին, № 12, հրապարակված 1987թ․-ին)։
Այս բառերը վերցված են Յա․ Ի․ Պերելմանի «Հետաքրքրաշարժ հանրահաշիվ» գրքից։ Ահա խնդրի օրինակ, որտեղ կարելի է կիրառել այդ դատողությունը։
m զանգվածով, 0°C ջերմաստիճանով սառույցի կտորը դրեցին 350 С ջերմաստիճանով և 2m զանգվածով ջրի մեջ։
Որոշեք ստացված խառնուրդի ջերմաստիճանը՝ ենթադրելով, որ ջերմափոխանակումը գնում է միայն ջրի և սառույցի միջև։
Հայտնի է, որ սառույցի հալման տեսակարար ջերմությունը 340կՋ/կգ է, իսկ ջրի տեսակարար ջերմունակությունը 4,2կՋ/(կգ·°C):
Ենթադրելով, որ ամբողջ սառույցը հալվել է՝ կստանանք 340m+4,2 x 3m t=4,2 m(35-t)
հավասարումը։
Այստեղից հետևում է, որ t<0.
Այս անհավասարությունը նշանակում է, որ ամբողջ սառույցը չի հալվել։
Ինչ-որ մի մաս այդպես էլ կմնա 0°C ջերմաստիճանով, իսկ ամբողջ ջուրը սառել է մինչև 0°C ջերմաստիճան։
Խառնուրդի ջերմաստիճանը կլինի 0°C աստիճան:
Իսկ հիմա հիշենք այսպիսի խնդիր ֆիզիկայից։
Խնդիր 2. Մարդը վազում է շարժասանդուղքով։ Առաջին անգամ նա հաշվեց 50 աստիճան, երկրորդ անգամ՝ արագությունը մեծացնելով երեք անգամ՝ նա հաշվեց 75 աստիճան։ Քանի՞ աստիճան կհաշվի մարդը, անշարժ շարժասանդուղքի դեպքում։
Այս խնդրի պայմանից ելնելով՝ նկատենք հետևյալը․
Մարդը վազում է ոչ թե շարժասանդուղքով, այլ շարժասանդուղքի «ժապավենով» ։
Շարժասանդուղքը մեծ և բարդ բարձրացնող-տեղափոխող մեքենա է։
Շարժասանդուղքի առաջին արտոնագրումը 1859 թվականին է եղել, իսկ առաջին գործող շարժասանդուղքը հայտնվել է 1894 թվականին Նյու Յորքում՝ որպես տուրիստական ատրակցիոն։ Մետրոյում այն առաջին անգամ կիրառվել է 1911 թվականին՝ Լոնդոնում։
Մեր երկրում առաջին շարժասանդուղքները գործածվեցին 1935 թվականին՝ Մոսկվայի մետրոյում։ Այդ պատճառով էլ այն առաջադրանքները, որտեղ մարդը վազում է շարժասանդուղքի վրայով, չէին կարող հայտնվել դպրոցական խնդիրների ժողովածուներում 1930 թվականներին և նույնիսկ 1940 թվականներին։
Այժմյան դպրոցականների մոտ հարցեր է առաջացնում այն հին խնդիրը, որտեղ ասվում է, որ վեց հնձվորներ շոգին ութ ժամում խմել են մի տակառ կվաս, քանի՞ հնձվոր կարող են նույն տակառը խմել երեք ժամում։
«Հնձվոր» բառը այսօր աշակերտներին նույնքան անծանոթ է, որքան «շարժասանդուղք» բառը նախորդ դարում նրանց պապիկներին ու տատիկներին։
Ուշադիր ընթերցողները հավանաբար արդեն նկատել են, որ առաջին հայացքից տարբեր թվացող այս երկու խնդիրները՝ 1-ը և 2-ը, իրականում մաթեմատիկորեն նույն խնդիրներն են։
Բացարձակ նմանությունը երևում է ստորև տրված աղյուսակից․
| Գետ | Շարժասանդուղքի «ժապավեն» |
| Գետի ափերը | Անշարժ շարժասանդուղքի պատերը |
| Նավամատույց A | Շարժասանդուղքի սկիզբը |
| Նավամատույց B | Շարժասանդուղքի վերջը |
| Շոգենավ կամ նավակ գետի վրա | Մարդը շարժասանդուղքի «ժապավենի» վրա |
| Լաստ գետի վրա | Կետ «ժապավենի» վրա, որը մարդու հետ միաժամանակ է հասնում ժապավենի վերջին |
| Գետի երկարությունը չափված կմ | Շարժասանդուղքի «ժապավենի» երևացող երկարությունը չափված աստիճաններով |
Պարզ է, որ լուծելով առաջին խնդիրը շոգենավի, նավակի, լաստի վերաբերյալ, մենք լուծել ենք նաև երկրորդ խնդիրը։ Այսպիսով` պատասխանը կլինի 100 աստիճան։
Առաջին խնդրում արված նկար 1- ը կարելի է ամբողջությամբ վերագրվել շարժասանդուղքի վերաբերյալ 2-րդ խնդրին։
Ընդ որում, մենք ենթադրում ենք, որ մարդը վազում է շարժասանդուղքի շարժման ուղղությամբ, սովորաբար հենց այդպես են վարվում շտապող ուղևորները։
Բայց խնդրի պայմանների մեջ ուղղակիորեն դա չի ասվում, դրա համար եկեք նայենք այն դեպքը, երբ մարդը վազում է շարժասանդուղքի շարժմանը հակառակ։
Ենթադրենք՝ շարժասանդուղքը շարժվում է վերևից ներքև, իսկ մարդը փորձում է բարձրանալ ներքևից վերև։
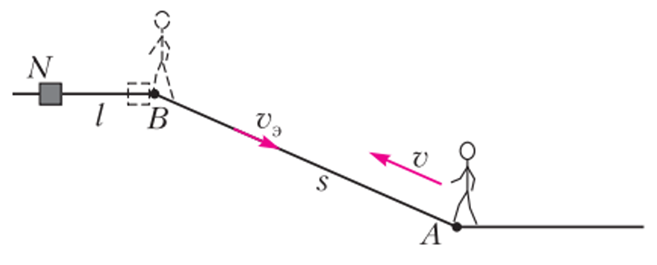
Նրա համար շարժասանդուղքը հանդես է գալիս որպես մարզասարք՝ վազքուղի։
Թող N-ը լինի շարժասանդուղքի սկզբում անտեսանելի այն աստիճանը, որը գտնվում է շարժասանդուքի սկզբի տեսանելի աստիճանից l հեռավորության վրա
Այդ աստիճանը և մարդը հանդիպում են շարժասանդուղքի վերևի կետում, դրա համար էլ կարող ենք կազմել հետևյալ հավասարումների համակարգը՝
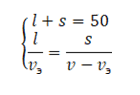
Մարդու 3v արագության դեպքում ստանում ենք այլ հավասարումների համակարգ՝
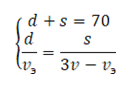
Այստեղ d-ն ուրիշ աստիճան է, որից մարդը իջնում է շարժասանդուղքից։ Համակարգերի առաջին հավասարումներից երևում է, որ l<d, երկրորդ հավասարումներից՝ հակառակը՝ l>d։
Հետևաբար, երկու համակարգերը անհամատեղելի են, և մարդը շարժասանդուղքի շարժմանը հակառակ վազելիս չի կարող պահպանել խնդրի պայմանները։
Նկատենք, որ այս եզրակացությանը կարելի է գալ շատ հեշտությամբ։
Շարժվելով շարժասանդուղքի շարժմանը հակառակ՝ ներքևից վերև, մարդը պետք է հաշվի առնի երևացող աստիճանները, նաև լրացուցիչ այն աստիճանները, որոնք կավելանան իր շարժման ժամանակ։
Մարդը մեծացնելով իր սեփական արագությունը, հասնում է վերև ավելի արագ, հետևաբար լրացուցիչ ավելացած աստիճանները կլինեն համեմատաբար ավելի քիչ։
Սկսելով այս աշխատանքը՝ մենք նպատակ ունեինք ընթերցողին համոզել, որ շարժասանդուղքի վրայով վազող մարդու մասին խնդիրը կարելի է և օգտակար է մեկնաբանել որպես նավի, շոգենավի, լաստի վերաբերյալ խնդիր։
Այս երկու խնդիրները հանդիսանում են «երկվորյակ» խնդիրներ, կարծես մեկը մյուսի արտացոլումը լինի։ Եթե խնդրում խոսվում է գետի և շոգենավի մասին, կարող ենք նկատի ունենալ մարդուն շարժասանդուղքի ժապավենին։
Կարելի է և հակառակը՝ գետի վերաբերյալ խնդիրները (և ընդհանրապես շարժումը) դիտարկել որպես շարժասանդուղքի հետ կապված խնդիրներ։
Օրինակի համար դիտարկենք այս խնդիրը։
Երկու ավտոմեքենա միաժամանակ դուրս եկան 420 կիլոմետր երկարությամբ երթուղի։ Առաջինը շարժվում էր 24 կմ/ժ -ով ավելի արագ, քան երկրորդը, և հասավ երթուղու վերջնակետ 2 ժամ շուտ, քան երկրորդը։ Գտե՛ք առաջին ավտոմեքենայի արագությունը։
Այս խնդիրը դիտարկելով որպես շարժասանդուղքի վերաբերյալ խնդիր՝ կլինի այսպես․
Շարժասանդուղքի երևացող աստիճանների քանակը 420 է։
Մարդը կանգնեց առաջին աստիճանի վրա և շարժվեց դեպի ներքև։
Միավոր ժամանակում նա 24 աստիճան ավելի է անցնում, քան շարժասանդուղքը։
Առաջին աստիճանը շարժասանդուղքով 2 միավոր ավելի երկար ժամանակում անցավ, քան մարդը։ Ի՞նչ արագությամբ է շարժվում շարժասանդուղքը։
Երկու խնդիրների համար մաթեմատիկական մոդելը լրիվ նույնն է։
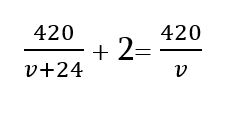
որտեղ v-ն շարժասանդուղքի արագությունն է։
Լուծելով հավասարումը՝ ստանում ենք v=60:
Այս դեպքում շարժասանդուղքի ժապավենի արագությունը միավոր ժամանակում կլինի 60 աստիճան, երկրորդ մեքենայի արագությունը՝ 60 կմ/ժ, առաջինի արագությունը՝ 84 կմ/ժ:
Շարժասանդուղքի վերաբերյալ խնդիրների լուծման դժվարությունը հնարավոր է, պայմանավորված է նրանով, որ աստիճանը միաժամանակ և՛ շարժասանդուղքի երկարության միավոր է, և՛ շարժասանդուղքի ֆիքսված կետ։ Հույս ունենք, որ մեր բացատրությունից հետո այլևս դժվարություններ չեն առաջանա։
Խմբագիր՝ Մարինե Ամիրջանյան