Թարգմանություն, մաս II
80-80-20 աստիճանային չափերով եռանկյան 60,70 աստիճաններով դեպքը
Դիցուք ունենք ABC հավասարասրուն եռանկյուն (AB = AC), որի ∠BAC = 20°։ D կետը AC կողմի վրա վերցված է այնպես, որ ∠CBD=60° է, Е կետը վերցված է AB կողմի վրա այնպես, որ ∠BCE = 70°։ Գտեք CED անկյան աստիճանային չափը (տե՛ս նկարը)։
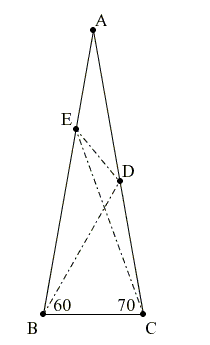
Լուծումները
Լուծում #1.
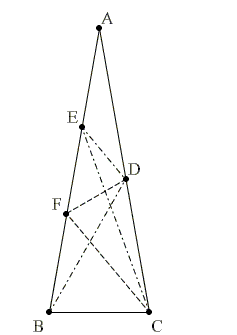
F կետը AB կողմի վրա նշենք այնպես, որ ∠BCF = 50°:
Խնդրի սկզբնական օրինակից (տե՛ս մաս I թարգմանությունը) մենք գիտենք, որ այդ դեպքում BDF անկյան աստիճանային չափը կլինի՝ ∠BDF = 30°։
Եռանկյուն BDF-ում ∠DBF = 20° և ∠BFD = 130°։
Եռանկյուն CFE-ում ∠ECF = 20°, ∠CEF = 30°, հետևաբար այդ երկու եռանկյունները նման են`
(1) DF/EF=BF/CF:
Քանի որ ∠BFC = 50°, ապա եռանկյուն BCF-ը կլինի հավասարասրուն է, BF = BC, ապա ∠DFE = 50°:
1․հավասարությունից հետևում է, որ եռանկյուն BCF և եռանկյուն DFE նման են, հետևաբար եռանկյուն DFE նույնպես կլինի հավասարասրուն, DF = DE։
Այստեղից էլ ∠DEF = 50° և ∠CED = ∠DEF — ∠CEF = 50° — 30° = 20°։
Պատասխան՝ 20°։
Լուծում#2.
Խնդրի այս լուծումը առաջարկել է Ռադու Իոնեսկուին։
F կետը AB կողմի վրա նշենք այնպես, որ ∠BCF = 50°:
Խնդրի սկզբնական օրինակից (տե՛ս մաս I թարգմանությունը) մենք գիտենք, որ այդ դեպքում CFD անկյան աստիճանային չափը կլինի՝ ∠CFD = 80°։
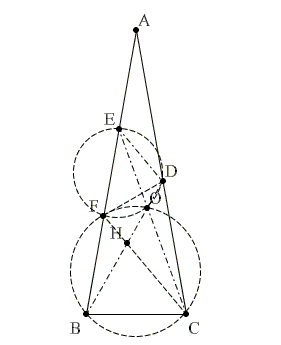
Դիցուք О կետը BD և CE հատվածների հատման կետն է, իսկ H ը՝ BD և CF հատվածների։ Այստեղից էլ ∠FBO = ∠FCO = 20°, քառանկյուն BCOF -ը ներգծված է շրջանագծին, մասնավորապես ∠OFC = ∠ OBC=60°։
Այստեղ էլ խնդրի սկզբնական օրինակից (տե՛ս մաս I թարգմանությունը) երևում է, որ ∠CFD = 80°, ինչը նշանակում է, որ ∠OFD = 20° է։
Եռանկյուն DFH-ում ∠HFD = (∠CFD) = 80°. ∠FHD = 70°։
Հետևաբար ∠FDH = 30°, այսինքն՝ FDO անկյունը նույնն է, ∠FDO = 30°։
Բայց մյուս կողմից էլ ∠FEO = ∠BEC = 30°։
Այսպիսով, քառանկյուն FODE-ն ներգծված է շրջանագծին և ∠CED = ∠OED = ∠OFD = 20°։
Պատասխան՝ 20°։
40-50 աստիճաններով դեպքը
Հեղինակային իրավունքը Ալեքսանդր Բոգոմոլնի, 1996-2018
Դիցուք ունենք ABC հավասարասրուն եռանկյուն (AB = AC), որի ∠BAC = 20°։ D կետը AC կողմի վրա վերցված է այնպես, որ ∠CBD=40° է, Е կետը վերցված է AB կողմի վրա այնպես, որ ∠BCE = 50°։ Գտե՛ք CED անկյան աստիճանային չափը (տե՛ս նկարը)։
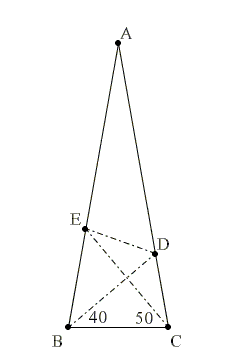
Սա սկզբնական խնդրի մեկ փոփոխված տարբերակն է, որը գործնականում շատ պարզ է լուծվում։
Քանի որ ∠BEC = 180° — 80° — 50° = 50°, ΔBCE-ն հավասարասրուն է։ Բացի այդ, ∠DBE = 80° — 40° = 40°, ինչը նշանակում է, որ BD-ն հավասարասրուն եռանկյան գագաթի անկյան կիսորդն է։ Այն նաև եռանկյան հիմքին տարված միջնագիծ է, ինչպես նաև՝ բարձրություն։
Այսպիսով, BD-ն ուղղահայաց է CE-ին և այն բաժանում է երկու մասի։
Կիրառելով այս պայմանը եռանկյուն CDE-ի համար՝ մենք կստանանք, որ DB-ն բարձրություն է, ինչպես նաև D գագաթից տարված միջնագիծ, ինչից հետևում է, որ եռանկյուն CDE-ն հավասարասրուն է, CD= DE, հետևաբար ստացանք ավելի կարևոր պայման՝ ∠CED = ∠DCE = 80° — 50° = 30°։
Պատասխան՝ 30°։

