Որոշ եռանկյուններ, իրենց հատկությունների շնորհիվ, դարձել են հետազոտությունների, զարմանքի, այլ խնդիրների առարկա։
Դրանցից մի քանիսը՝ հավասարակողմը, հավասարասրուն ուղղանկյունը, ոսկեն, եգիպտականը և 30-60-90 աստիճանային չափեր ունեցողը, լավ հայտնի են։
Կա մի եռանկյուն, որը, հավանաբար, ավելի շատ է արժանի ուշադրության․ մուտք է գործել մաթեմատիկական աշխարհ մոտ 100 տարի առաջ։
Բերքլիի Մաթեմատիկական խմբակներից Թոմ Ռայքը հիշատակում է այս խնդրի հայտնվելու մասին մաթեմատիկական ամսագրի 11-րդ համարում, (1922 թ.), էջ 173։ (Նրա օնլայն հոդվածում ներկայացված են նաև լրացուցիչ հղումներ)։
Այս եռանկյունը 80-80-20 աստիճանային չափերով եռանկյուն է (կամ երբեմն՝ 20-80-80 չափերով), այսինքն՝ հավասարասրուն եռանկյուն է, որի գագաթի անկյունը 20° է, իսկ հիմքին առնթեր անկյունները՝ 80°:
Սկզբնական խնդրից ծնվել են մի քանի տարբերակներ, և դրանցից յուրաքանչյուրը լուծվել է տարբեր եղանակներով։
Ես կավելացնեմ լուծումները նաև այն խնդիրները, որոնք առնչվում են սկզբնական խնդրի հետ։ Ցանկացած օգնություն ողջունելի է։
Այս էջը ծառայելու է որպես այս նախաձեռնության գլխավոր հարթակ։
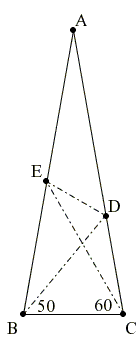
Դիցուք ունենք ABC հավասարասրուն եռանկյուն (AB = AC), որի ∠BAC = 20°։ D կետը AC կողմի վրա վերցված է այնպես, որ ∠CBD=50° , Е կետը վերցված է AB կողմի վրա այնպես, որ ∠BCE = 60°։ Գտեք ∠CED -ի աստիճանային չափը։
Լուծում # 1
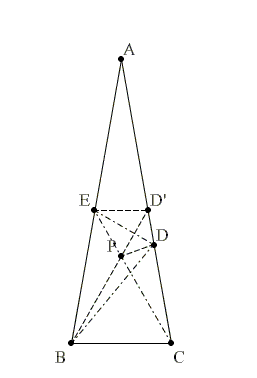
AC կողմի վրա D’ կետը վերցնենք այնպես, որ ED’ ||BC։
Դիցուք BD’ հատվածը հատում է CE հատվածը P կետում, տե՛ս նկարը։ Եռանկյուն BCP-ն հավասարակողմ է, CP = BC։ Եռանկյուն BCD-ն հավասարասրուն է, BC = CD։ Եռանկյուն CDP հավասարասրուն է՝
∠CPD = 80°, ∠DPD’ = 40°
Այսպիսով, ∠DD’P = 40°, եռանկյուն DPD’ հավասարասրուն է և DP = DD’. Այսինքն՝ ΔEPD’ հավասարակողմ է, EP = ED’։
Այստեղից էլ կունենանք ΔDED’ = ΔDEP, DE-ն ∠D’EP կիսորդն է, կստանանք՝ ∠CED = ∠PED = 30°։
Պատասխան՝ 30°։
Լուծում 2
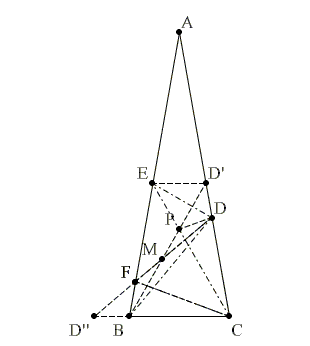
Կից խնդրի ապացույցի հեղինակն ՝ Մարիանո Պերես դե լա Կրուսը (related problem)։
Տանենք CF-ը, F կետը ընկած է AB -ի վրա, ∠BCF = 20°։ Եռանկյուն BFC -ը հավասարասրուն եռանկյուն է, BC = CF։
Եռանկյուն BCD-ն նույնպես հավասարասրուն է, որովհետև ∠BDC = 180° — 80° — 50° = 50° = ∠CBD, այստեղից էլ BC = CD և CD = CF։ Հետևաբար ΔCDF հավասարասրուն եռանկյուն է, որի գագաթի անկյունը ∠DCF = 60° է, այսինքն՝ ΔCDF նաև հավասարակողմ է։
Դիցուք ∠CBD’ = 60° , որտեղ D’ ընկած է AC-ի վրա։
P կետը BD’ և CE հատվածների հատման կետն է։
Եռանկյունի CPB հավասարակողմ է և, C-ի շուրջը պտտվելով, արտապատկերվում է ΔCDF-ի վրա։
Այտեղից էլ M կետը DF և BP հատվածների հատման կետն է, իսկ CM-ը ∠ACB-ի կիսորդն է։
Այժմ դիտարկենք արտապատկերումը CM ուղիղի նկատմամբ։ D-ն արտապատկերվում է B-ի վրա, իսկ P-ն՝ F-ի վրա։ Թող D′-ն արտապատկերվի D′′-ի վրա, և D′′- ը կընկնի BC-ի շարունակության վրա։
Կունենանք՝
∠CFD՛՛(= ∠CPD’) = 120°, ∠FCD” = 20°.
Այստեղից էլ
∠CD”F = 40°. ∠FBD” = 100°, ∠BFD” = 40° և Δ BFD” հավասարասրուն է՝
BF = BD”, հետևաբար՝ DP = DD’.
Քանի որ եռանկյունի EPD’-ն հավասարակողմ է, իսկ քառանկյուն EPDD’-ի անկյունագծերը ուղղահայաց են միմյանց, հետևում է, որ ED-ն ∠PED’-ի կամ ∠PDD’-ի կիսորդն է։ Մասնավորապես, ∠PED = 30°։
Այլ կերպ՝ ∠CED = 30°։
Պատասխան՝ 30°։
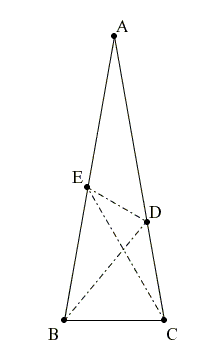
∠CED-ն նշանակենք x-ով, ∠CDE-ն կլինի ՝ ∠CDE= 160° — x։
Գրենք սինուսների թեորեմը CDE եռանկյան համար։
CE : CD = sin (160° — x) : sin x
CE : BC = sin 80° : sin 40° = 2cos 40°
Գրենք նաև BCE եռանկյան համար՝
CE : BC = sin 80° : sin 40° = 2cos 40°
Հիշենք, որ sin 2α = 2sin α · cos α
Եռանկյուն BCD-ն հավասարասրուն է, որի սրունքներն են՝ CD = BC, ինչն էլ մեզ թույլ է տալիս գրել եռանկյունաչափական հավասարումը՝
sin (160° — x) : sin x = sin 80° : sin 40°
Օգտագործելով հետևալ հավասարումը, կստանանք՝ sin (180° — α) = sin(α),
sin (20° + x) = 2cos 40° · sin x = 2cos (60° — 20°) · sin x.
Օգտագործելով սինուսի գումարման բանաձևը և կոսինուսի գումարման բանաձևը`
sin 20° · cos x + cos 20° · sin x = cos 20° · sin x + √3sin 20° · sin x,
պարզեցնելով կստանանք՝
sin 20° · cos x = √3sin 20° · sin x,
կամ ctg x = √3.
որտեղից էլ x = 30°.
Պատասխան՝ 30°։
Լուծում # 4
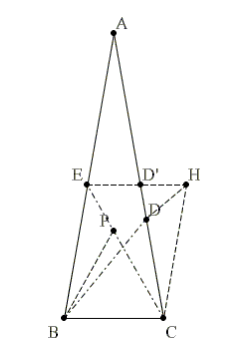
E կետով տանենք BC կողմին զուգահեռ ուղիղ և C կետով տանենք АB-ին զուգահեռ ուղիղ։
Հատման կետը նշանակենք H-ով, նկատենք, որ BCHE քառանկյունը զուգահեռագիծ է։
EC հատվածի վրա P կետը վերցնենք այնպես, որ եռանկյուն BPC լինի հավասարակողմ եռանկյուն։
Հետևաբար BP = BC = CD և BE = CH. ∠EBP = 20° և ∠HCD = 20°, այդ պատճառով էլ եռանկյունների հավասարության հայտանիշի համաձայն,
ΔEBP = ΔHCD. հետևաբար ∠CHD = ∠BEC = 40°.
Քանի որ ∠CHE = 80°, HD-ն CHE անկյան կիսորդն է։
Մյուս կողմից, CD-ն ∠ECH անկյան կիսորդն է։
Այսպիսով, D կետը հանդիսանում է ECH եռանկյանը ներգծված շրջանագծի կենտրոնը, որը կիսորդների հատման կետն է։
Ուստի, DE-ն ∠CEH անկյան կիսորդն է, և ∠CED = 30°։
Պատասխան՝ 30°։
Լուծում # 5
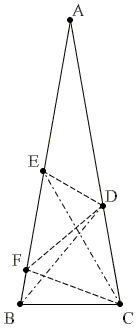
AB կողմի վրա F կետը վերցնենք այնպես, որ ∠BCF = 20°։
Այնուհետև կստանանք ∠BFC = 80° = ∠ABC, այսպիսով եռանկյուն BCF-ը հավասարասրուն է, և CF = BC։
Ունենք CD = BC և ∠DCF = 60°, ΔCDF -ը հավասարակողմ եռանկյուն է, և մասնավորապես DF = CF.։
ΔCEF հավասարասրուն է, քանի որ ∠CEF = ∠ECF = 40°, հետևաբար DF = EF։
Ստացանք, որ F կետը հավասարահեռ է C, D, և E կետերից, ուրմեն այն հանդիսասնում է ΔCDE-ի արտագծած շրջանագծի կենտրոն։
∠CED-ն կլինի F կենտրոնով շրջանագծի ներգծյալ անկյուն, որը հենված է նույն աղեղի վրա, ինչ որ կենտրոնային անկյուն CFD-ն։ Մենք գիտենք, որ այն 60° է, հետևաբար ∠CED = 30°։
Պատասխան՝ 30°։
Լուծում # 6
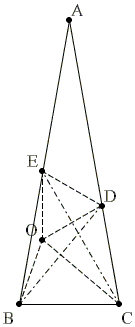
Դիցուք Օ-ն ΔBDE-ին արտագծած շրջանագծի կենտրոնն է։
Ներգծյալ անկյուն ∠DBE = 30° է և հենված է նույն աղեղի վրա, ինչպես կենտրոնային անկյուն <DOE ։
Ուրեմն ∠DOE = 60° և եռանկյուն DOE-ն հավասարակողմ է։ Մասնավորապես ∠DEO = 60° և EO = DE։
Եռանկյուններ BDO-ն և BCD-ն հավասարասրուն են, ինչից էլ բխում է, որ CO-ն ∠BCD-ի կիսորդն է։ Հետևաբար ∠DCO = 40°, այսինքն՝ ∠DCE = 20°, CE-ն ∠DCO-ի կիսորդն է։
Այժմ դիտարկենք CDE և COE եռանկյունները, EO = ED, CE ընդհանուր կողմ է, և ∠DCE = ∠OCE։
Մենք կարող ենք պնդել, որ եռանկյուն CDE և եռանկյուն COE հավասար են, բայց այդպիսի հայտանիշ գոյություն չունի եռանկյունների հավասարության հայտանիշների մեջ՝ երկու կողմերով և դրանցից մեկի դիմացի անկյունով։
Սովորաբար (կողմ, կողմ, անկյուն) պայմանը բավարար չէ եռանկյուն կառուցելու համար, քանի որ E կետում կարող են գոյություն ունենալ երկու հնարավոր անկյուններ՝ հաշվի առնելով տրված կողմերն ու անկյունը C-ում, մեկը փոքր է 90°-ից, իսկ մյուսը՝ մեծ։
Սակայն այս դեպքում նախորդ պարբերություններից մենք գիտենք, որ երկու եռանկյուններում էլ E կետում գտնվող անկյունները փոքր են 60°-ից։
Այս հանգամանքը թույլ է տալիս հաստատել, որ △CDE=△COE։
Այս եզրակացությունից հետևում է, որ CE-ն կիսում է նաև ∠DEO-ն, ուստի ∠CED = 30°։
Պատասխան՝ 30°։
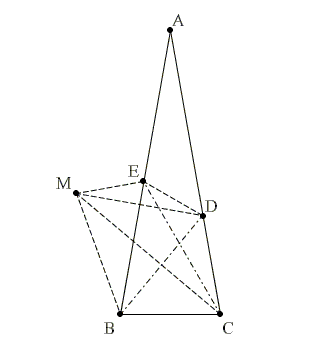
Դիցուք M կետը <BCD-ի կիսորդի վրա վերցված այնպիսի կետ է, որ ∠ABM = 30° է։
Քանի որ եռանկյուն BCD-ն հավասարասրուն է (BC = CD), ապա CM-ը BD հատվածի միջնուղղահայացը կլինի, այսինքն՝ BM = DM։ M կետի ընտրությունից հետևում է, որ ∠DBM = 60°, ուստի եռանկյուն BDM-ը հավասարակողմ է։ Քանի որ BE-ն ∠DBM-ի կիսորդն է, այն նաև DM հատվածի միջնուղղահայացն է։
Դիտարկենք եռանկյունի CDM-ը, E-ն DM միջնուղղահայացի և C անկյան կիսրոդի հատման կետն է։
Հետևաբար, E կետը պատկանում է եռանկյուն CDM-ի արտագծած շրջանագծին։
Այդ շրջանագծի երկու ներգծյալ անկյուններ իրար հավասար են՝ <CEDև <CMD-ն, բայց ∠CMD-ն հավասար է ∠BMD անկյան կեսին, ուստի ∠CED = 30°։
Պատասխան՝ 30°։
Լուծում # 8
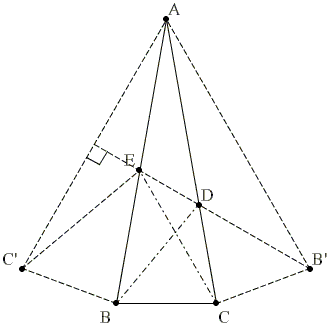
Այս լուծումը բխում է 7-ից, որի հեղինակը Ալեքսանդր Կորնիենկոն է (այն ժամանակ` դպրոցական)։
AC ուղղի նկատամամբ B կետի համաչափը նշանակենք B’, իսկ C կետի համաչափը AB ուղղի նկատամամբ՝ C’:
Այժմ ∠AB’D = ∠ABD = 30°
Բացի այդ ∠B′AC′ = 60°, և AB′ = AC′, հետևաբար B′D-ն AC′ հատվածի միջնուղղահայացն է։
∠CED = 180° — 40° — 40° — 70° = 30°
(Այս լուծումը խնամքով ներառված է 18-անկյուն բազմանկյան պատկերի մեջ)։
Պատասխան՝ 30°։
Լուծում # 9
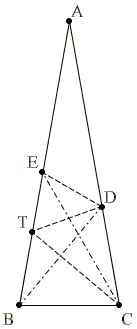
Այս լուծումը բխում է 8-ից, որի հեղինակը Սերգեյ Սապրիկինն է (այն ժամանակ՝ դպրոցական)։
T կետով նշանակենք անկյուն ACB-ի կիսորդի և AB կողմի հատման կետը։
Հետևաբար, ∠BTC = 60°, և BC = CD, հետևաբար ΔBCT = ΔDCT.
Դիտարկենք եռանկյուն CDT, E-ն անկյուն C-ի կիսորդի և անկյուն T-ի արտաքին անկյան կիսորդի հատման կետն է։
E-ն եռանկյուն CDT-ի առգծված շրջանագծի կենտրոնն է, hետևաբար, DE հատվածը եռանկյան D անկյան արտաքին անկյան կիսորդն է։ Բացի այդ, ∠BDT = ∠DBT = 30°։
Այնուհետև, ∠CDT = 80°, ուստի ∠EDT = (180° — 80°) / 2 = 50°։
Եվ վերջապես՝
∠CED=180°−20°−50°−30°−50°=30°։
Պատասխան՝ 30°
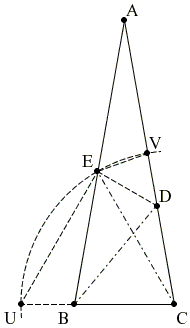
Խնդիրը լուծեց Լուկ Ռեպլին։
Տանենք EC շառավղով շրջանագիծ, որը BC կողմը կհատի U կետում, իսկ AC կողմը՝ V կետում։
Եռանկյուն CEU-ն հավասարասրուն եռանկյուն է, CE=CU, քանի որ <BCE=60°, ապա նաև հավասարակողմ է, և EU = CE և ∠CEU = 60°.
Հետևաբար ∠BEU = 20°։
Մյուս կողմից՝ AE = CE, այսինքն՝ եռանկյուն ACE հավասարասրուն է, ուրեմն հիմքի անկյունները հավասար են՝ <A= <C= 20°:
Դիտարկե՛նք BEU և VAE եռանկյունները:
- AE = EU, քանի որ երկուսն էլ հավասար են CE-ին
- AV = BE, որովհետև AV = AC — CV = AB — AE = BE
- ∠EAV = ∠BEU, քանի որ երկուսն էլ հավասար են 20°։
Եռանկյունների հավասարության հայտանիշի համաձայն՝ այդ երկու եռանկյունները հավասար են՝ EV = BU։
Մյուս կողմից, քանի որ ΔBCD հավասարասրուն է, BC=CD, հետևաբար BU = CU — BC = CV — CD = DV.
Այդտեղից էլ VD = EV, եռանկյուն DEV հավասարասրուն է։
Այժմ՝ ∠DVE = 180° — ∠AVE = 180° — ∠EBU = ∠ABC = 80°։
Այսպիսով, ∠DEV = (180° — 80°)/2 = 50°, հաշվելով CED անկյան աստիճանային չափը՝ կստանանք՝ ∠CED = 30°։
Պատասխան՝ 30°։
Լուծում #11
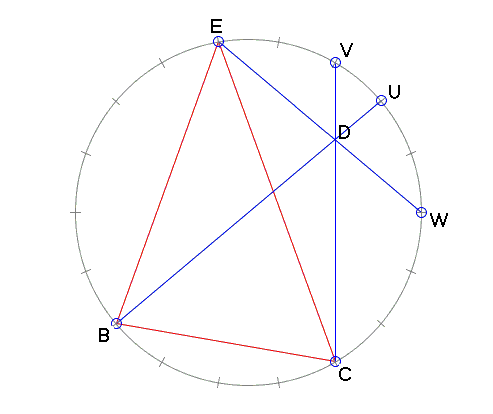
Խնդրի լուծման հիմքում ընկած է Չևիի թեորեմը (եռանկյունչափության համար, տես այստեղ` Պրասոլով, էջ 34-35):
Պատկերացրե՛ք՝ շրջանածի վրա նշված են կանոնավոր 18-անկյան գագաթները։
Մի քանի լարեր՝ BU, CV, EW, հատվում են մի կետում, նշանակենք այն D-ով։ Օգտվելով Պրասոլովում առաջարկած Չևիի թեորեմից` տեսնում ենք հետևյալ նույնությունը, որն էլ պատրաստվում ենք ապացուցել։
sin(20°)·sin(50°)·sin(70°) = sin(30°)·sin(30°)·sin(80°),
Կան եռանկյունաչափական մի քանի կարևոր բանաձևեր, հիշենք դրանք՝
sinα sinβ = ½(cos(α — β) — cos(α + β)), and
sinα cosβ = ½(sin(α + β) — sin(α — β)), and
Երկուսն էլ գումարման և հանման բանաձևերի պարզ հետևանքներն են`
Այսպիսով՝
sin(30°)·sin(30°) = ½(1 — cos(60°)) = 1/4 և
sin(20°)·sin(50°) = ½(cos(30°) — cos(70°)), Չևիի թեորեմի համաձայն
2 sin(70°)·(cos(30°) — cos(70°)) = sin(80°).
Վերը նշված բանաձևը նորից կիրառելով՝ կստանանք՝
| 2 sin(70°)·(cos(30°) — cos(70°)) | = sin(100°) + sin(40°) — sin(140°)) | |
| = sin(80°) + sin(40°) — sin(40°)) | ||
| = sin(80°), |
Այստեղ մեզ անհրաժեշտ եղավ հետևյալ կապը՝ sin(180° — γ) = sin(γ)։
Նկատենք, որ եթե շարունակենք BE և CV կողմերը մինչև դրանց հատվելը A կետում, ապա ստացված նկարը սիրուն կհամընկնի սկզբնական խնդրի նկարի հետ։ Սա թույլ է տալիս ասել, որ ∠CED ներգծյալ անկյուն է, որը հենված է 60° աղեղի վրա, այսինքն՝ ∠CED=30° է։
Պատասխան՝ 30°։
Հղում
- V. V. Prasolov, Essays On Numbers And Figures, AMS, 2000
Վ. Վ. Պրասոլով, «Թվերի և պատկերների մասին էսսեներ», (AMS), 2000 թ. - Լուծում #12.ժ
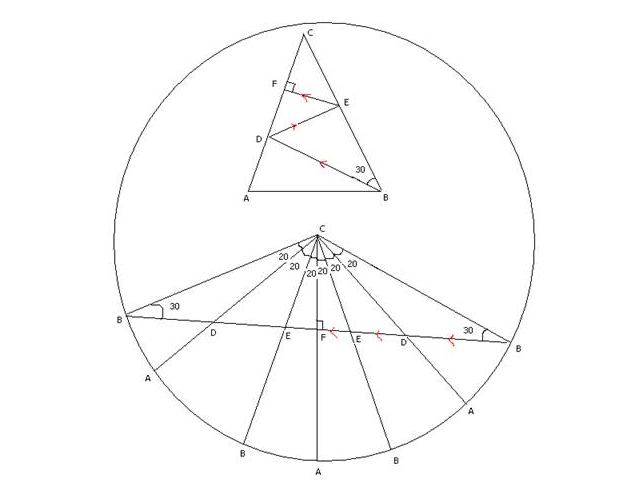
Ես այս լուծումը վերցրել եմ StackExchange․com էջից։
StackExchange էջում գրառումը հրապարակված է Արաբհատա անունով։
Դուք կնատեք, որ Արաբհատան գագաթների համար օգտագործում է տառեր, որոնք տարբերվում են մեր էջում օգտագործած տառերից։ Հուսով եմ՝ զգալի շփոթություն չի առաջացնի։
Մենք տեսնում ենք, որ 80-80-20 եռանկյունը ոչ այլ ինչ է, եթե ոչ 18 կողմ ունեցող կանոնավոր բազմանկյան մի մասը, որի 6 եռանկյունները ցուցադրված են վերևի շրջանագծի ներքևի մասում:
Այժմ դիտարկենք 80-80-20 եռանկյունը (ABC-ն նկարի վերևի մասում է) և լույսի ճառագայթ գցենք հիմքի գագաթներից մեկից (նկարում B գագաթից ) հիմքի նկատմամբ 50 աստիճան անկյան տակ (կամ 30 աստիճան կողմերից մեկից)։ (Տե՛ս շրջանագծի վերևում պատկերված եռանկյունը և կարմիր կետերը)։
Կարող ենք ցույց տալ, որ ճառագայթը կանդրադառնա երկու անգամ (առաջինը՝ D կետում, երկրորդը՝ E կետում) և երրորդ անգամ կընկնի 90 աստիճան անկյան տակ (F կետում), այսինքն՝ 5 անդրադարձումից հետո լույսի ճառագայթը կվերադառնա գագաթ։
Այս անդրադարձման գործընթացը կարելի է պատկերացնել այլ կերպ․ յուրաքանչյուր անգամ անդրադարձնել ոչ թե ճառագայթը, այլ եռանկյունը (տե՛ս նկարի ներքևի մասում պատկերված 6 եռանկյուններում կարմիր սլաքները)։
Այժմ անդրադարձման երրորդ կետը՝ F-ը (այսինքն՝ 90 աստիճան անկյան տակ ընկնող կետը), հենց այն կողմի միջնակետն է, որի վրա ճառագայթն ընկնում է։ Դա կարելի է տեսնել՝ դիտելով նկարի ներքևի մասը։
Դիտարկենք ամենաաջ B կետը և համապատասխան CBF եռանկյունը։ Սա 90-60-30 աստիճանով եռանկյուն է։ Այսպիսով, CF-ը CB-ի կեսն է, որն էլ CA-ի կեսն է։
(Վերադառնանք վերևում գտնվող եռանկյանը), այսինքն՝ F-ը AC-ի միջնակետն է։ Այսպիսով, ACE եռանկյունը հավասարասրուն է, հետևաբար CAE անկյան աստիճանային չափը 200 է։
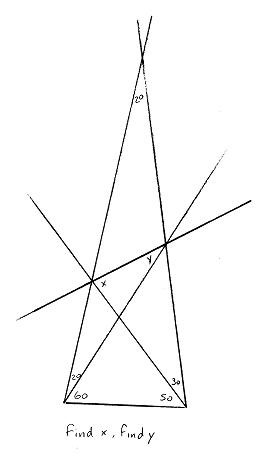
Այսպիսով, մենք տեսնում ենք, որ BDE անկյունը պետք է լինի խնդրի x անկյունը, որը կլինի
180°-(50°+50°) = 80° (քանի որ DE-ն BD-ն է՝ անդրադարձած AC-ի վրա)։
Այդ y անկյունը 30 աստիճան է, հետևաբար․․․
Ցուցում։ x-ի և y-ի մասին ավելի շատ պատկերացում կազմելու համար, տե՛ս ներքևի նկարը՝
Անգլերենից թարգմանեց Լիանա Հակոբյանը։
Նյութի հղումը՝ այստեղ․․․
Խմբագիր՝ Արևիկ Ներսիսյան

