Շրջանագծի շառավղի և կողմի կազմած անկյունը «Կվանտ» ամսագիր, 2025, թիվ 3
Հեղինակներ՝ Յու. Բլինկով, Դ. Շվեցով
Թարգմանությունը՝ Աննա Պետրոսյանի
Հիմնական փաստը
Արդյո՞ք հնարավոր է լուծել բարդ օլիմպիական խնդիր՝ ունենալով միայն այն գիտելիքները, որոնք ընդգրկված են 8-րդ դասարանի առաջին կիսամյակի ծրագրում։ Եվ առանց հատուկ «օլիմպիական» փաստերի ու հնարքների իմացության։
Պարզվում է՝ շատ դեպքերում բավական է լավ տիրապետել սովորական դպրոցական նյութին։ Եկեք դիտարկենք մի պարզ խնդիր։
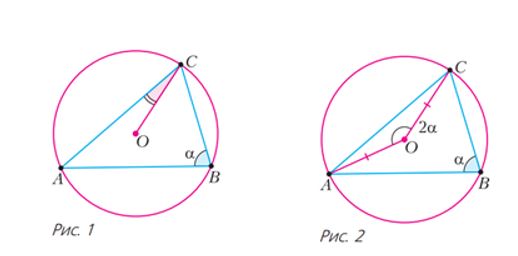
O կետը սուրանկյուն եռանկյուն ABC-ին արտագծած շրջնագծի կենտրոնն է։ Գտեք ∠ACO-ն, եթե ∠ABC=α (տես նկ. 1)։
«Իսկ ի՞նչ հետաքրքիր բան կարող է լինել այստեղ», — կասի ընթերցողը։
Իրոք, ներգծված անկյունը հավասար է նույն աղեղին հենված կենտրոնական անկյան կեսին (տես նկ. 2), այսինքն՝ եթե ∠ABC=α < 900 ապա ∠AOC=2α, ուստի ∠ACO=900 − α ։
Պա՞րզ է։ Իհարկե։ Բայց հենց սա է մեր հոդվածի հիմնական փաստը, որի շնորհիվ մենք կկարողանանք լուծել մի քանի բարդ խնդիրներ։ Հետագայում մենք այն կկոչենք շառավղի և կողմի կազմած անկյուն։
Հիմնական փաստ։ O կետը սուրանկյուն եռանկյուն ABC-ին արտագծած շրջագծի կենտրոնն է։
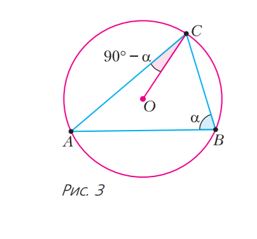
Այդ դեպքում ∠ACO=90∘−∠ABC (տես նկ. 3)։
Առաջադրանք 2
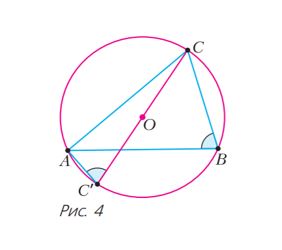
1․ Վերականգնեք հիմնական փաստի մեկ այլ ապացույցը՝ ըստ նկ. 4-ի։
2. Ինչպե՞ս կփոխվի հիմնական փաստը, եթե ∠ABC -ն լինի բութ անկյուն։
Ինչպե՞ս կարելի է օգտագործել այս փաստը։ Բանն այն է, որ այն ցույց է տալիս եռանկյանն արտագծած շրջագծի կենտրոնի դիրքը։ Դպրոցական ծրագրում սովորաբար ապացուցվում է, որ եռանկյանն արտագծած շրջանագծի կենտրոնը հավասարահեռ է եռանկյան գագաթներից, այսինքն՝ գտնվում է եռանկյան կողմերին տարված ուղղահայացների հատման կետում։
Բայց եթե, օրինակ, եռանկյուն ABC-ի B անկյունը հաստատուն է, ապա շրջանագծի կենտրոնը նույնպես գտնվում է այնպիսի ուղու վրա, որը AC կողմի հետ կազմում է հաստատուն անկյուն։
Դիտարկենք հետևյալ խնդիրը
Խնդիր 1։ AL-ը հավասարասրուն եռանկյուն ABC (որտեղ AB=BC) անկյան կիսորդն է, որը հատում է եռանկյանն արտագծած շրջագիծը W կետում։ I կետը այդ եռանկյանն արտագծած շրջանագծի կենտրոնն է։ Ապացուցեք, որ եռանկյուն IBW-ին արտագծած շրջագծի կենտրոնը գտնվում է BC կողմի վրա (տես նկ. 5)։
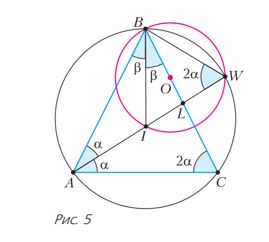
Լուծում։ Նկատենք, որ BI ուղիղը B անկյան կիսորդն է։ Նշենք՝ ∠BAC = ∠BCA = 2α, ∠ABC = 2β։ Այդ դեպքում՝ ∠IWB = ∠AWB = ∠ACB = 2α, օգտագործելով նույն աղեղին հենված ներգծված անկյունների հավասարության փաստը։
1․ Եթե O կետը սուրանկյուն եռանկյուն IBW-ին արտագծած շրջանագծի կենտրոնն է։ Այդ դեպքում՝ ∠IBO=90∘−2α, ըստ հիմնական փաստի։ Մյուս կողմից՝ ∠IBL=∠IBC=β
Մնում է նկատել, որ 2α+β=90∘, այսինքն՝ O կետը գտնվում է BC ճառագայթի վրա և եռանկյուն IBW ներսում։
Խնդիրը լուծված է։
2005 թվականից սկսած ամեն ամառ՝ հուլիսի վերջին, անցկացվում է Ի․ Ֆ․ Շառիգինի անվան երկրաչափության օլիմպիադայի եզրափակիչ փուլը։ Ընդհանրապես, այս օլիմպիադայի խնդիրները բարդ են նույնիսկ փորձառու դպրոցականների համար։ Հաջորդ խնդիրը (կետերի երկրաչափական դիրքի տերմիններով) առաջարկվել է իններորդ դասարանցիներին 2010 թվականի եզրափակիչ փուլում։
Խնդիր 2։ ABC -ն սուրանկյուն եռանկյուն է։ Ցանկացած ուղիղ, որն անցնում է B գագաթով, հատում է AC կողմը K կետում, իսկ եռանկյուն ABC-ին արտագծած շրջանագիծը՝ M կետում։ Ապացուցեք, որ բոլոր այդպիսի AMK եռանկյուններին արտագծած շրջագծերի կենտրոնները գտնվում են միևնույն ուղիղի վրա (տես նկ. 6)։
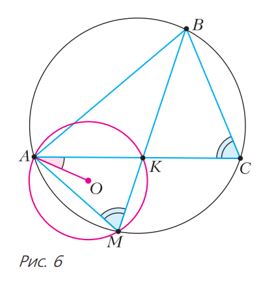
Լուծում։ Նկատենք, որ ∠AMK=∠AMB=∠ACB, այսինքն՝ այն հաստատուն է և սուր։ O կետը եռանկյուն AMK-ին արտագծած շրջանագծի կենտրոնն է։ Այդ դեպքում՝ ∠OAK= 90∘ − ∠ACB, ըստ հիմնական փաստի, այսինքն՝ նույնպես հաստատուն է։ Բացի այդ, O և M կետերը գտնվում են AC ուղղի նկատմամբ նույն կիսահարթության մեջ։ Հետևաբար, O կետը գտնվում է հաստատուն ճառագայթի վրա, որի սկիզբը A կետն է։ Ինչն էլ պետք էր ապացուցել։
Առաջադրանք 3
Գտե՛ք այդպիսի կենտրոնների երկրաչափական դիրքը։
Նախորդ խնդիրների պայմաններում հիշատակվում էր շրջագծի կենտրոնը։
Զգալիորեն բարդ է դառնում, երբ պայմանում դրա մասին ոչինչ նշված չէ։
Խնդիր 3։ Ունենք ABCD ուռուցիկ քառանկյուն, որի մեջ ∠ABD=∠CDB=60∘, ∠BCA=∠CAD=30։ Գտե՛ք BD-ի երկարությունը, եթե AB=2 (նկ. 7):
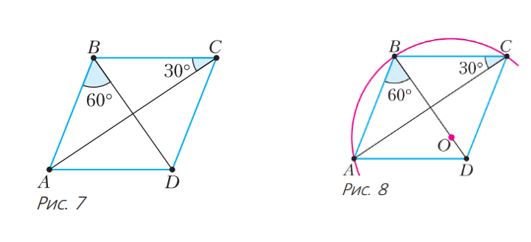
Լուծման ուղի։ Նկատենք, որ ABCD քառանկյունը զուգահեռագիծ է։ Սակայն նրա անկյունները կամ որևէ եռանկյան անկյուններ ուղղակի հաշվել հնարավոր չէ։ Բայց կան անկյուններ, որոնք լրացնում են միմյանց մինչև 900, ընդ որում՝ դրանցից մեկը եռանկյան անկյուն է, իսկ մյուսը դրված է այն ճառագայթից, որը պարունակում է զուգահեռագծի հակադիր կողմը։ Այս դիտարկումից ելնելով՝ փորձենք դիտարկել եռանկյանն արտագծած շրջագիծը։
Լուծում։ O կետը եռանկյուն ABC-ին արտագծած շրջանագծի կենտրոնն է (տես նկ. 8)։
Այդ դեպքում ∠ABO = 90° − ∠ACB = 60° = ∠ABD = 60°, այսինքն՝ O կետը գտնվում է BD ճառագայթի վրա։ Մյուս կողմից, O կետը գտնվում է AC անկյունագծի միջնուղղահայացի վրա (ինչո՞ւ): Հնարավոր են երկու տարբերակ՝
O կետը համընկնում է զուգահեռագծի ABCD անկյունագծերի հատման կետին, այսինքն՝ զուգահեռագիծը ուղղանկյուն է, և BD = 2AB = 4։
Միջնուղղահայացը համընկնում է BD ուղիղի հետ, այսինքն՝ ABCD-ն շեղանկյուն է, և BD = AB = 2, որպես հավասարակողմ եռանկյան կողմ։
Խնդիրը լուծված է։
Նկատենք, որ այս խնդրում մենք շրջանագծի կենտրոնը գտանք այսպես. վերցրինք եռանկյան գագաթից դուրս եկող ճառագայթ, որը կազմում է տրված անկյուն, և գտանք դրա հատումը կողմին տարված միջնուղղահայացի հետ։ Այս հնարքը մենք կօգտագործենք ևս մեկ անգամ։
Բարձրություններին
Դե ինչ, հիմնական փաստը պարզեցինք, դիտեցինք առաջին օրինակները։ Իսկ հետո՞։ Ո՞ր անկյունն է ևս լրացնում եռանկյան անկյունը մինչև 90°։ Իհարկե, այն անկյունը, որը գոյանում է եռանկյան կողմի և մյուս կողմին տարված բարձրության միջև։ Այսքանից ելնելով՝ կարելի է ձևակերպել հետևյալը։
CC՛ -ն սուրանկյուն եռանկյուն ABC-ի բարձրությունն է (տես նկ. 9)։ O կետը եռանկյանն արտագծած շրջագծի կենտրոնը։ Այդ դեպքում ∠ACO=∠BCC՛, այսինքն՝ CO և CC՛ ուղիղները համաչափ են ABC եռանկյան C գագաթի անկյան կիսորդի նկատմամբ։
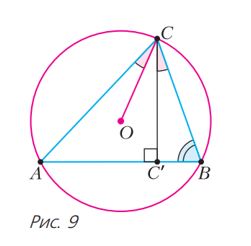
Ապացույց։ Նկատենք որ, ∠ABC=α, ապա ∠BCC′=90∘−α=∠ACO ։
Հետևանք 1-ը ճիշտ է նաև բութանկյուն եռանկյան դեպքում։ Ինչպե՞ս կփոխվի ապացույցը։
Եկե՛ք դիտարկենք այս հետևանքի կիրառումը։ Յոթերորդ դասարանի աշակերտների համար հասանելի է նման խնդիրը։
Առաջադրանք 4։ Ունենք ABC ուղղանկյուն եռանկյան, որի մեջ CM-ը միջնագիծ է, CH բարձրությունը ուղղահայաց է AB կողմին։ Ապացուցեք, որ ACM=
BCH։
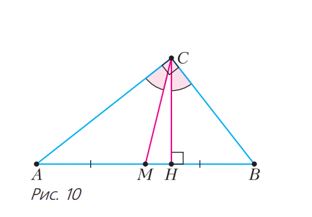
Հակադարձ խնդիրը, ինչպես հաճախ պատահում է, զգալիորեն ավելի բարդ է լինում։
Խնդիր 4։ ABC -ն ոչ հավասարասրուն եռանկյուն է (տես նկ. 11), որի մեջ տարված են՝
CM միջնագիծը և CH բարձրությունը, որտեղ H կետը գտնվում է AB հատվածի վրա։
Ապացուցել, որ եթե ∠ACM=∠BCH, ապա ∠ACB=900։
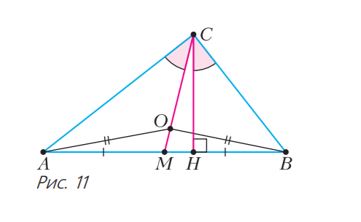
Լուծում։
Ապացուցենք, որ M կետը եռանկյանն արտագծած շրջանագծի կենտրոնն է, ինչից էլ կբխի խնդրի պահանջը։ O կետը եռանկյուն ABC-ին արտագծած շրջանագծի կենտրոնը։ Այդ դեպքում ∠ACO=∠BCH, այսինքն՝ O կետը գտնվում է CM ճառագայթի վրա։ Մյուս կողմից, O կետը գտնվում է AB կողմի միջնուղղահայացի վրա։
Քանի որ եռանկյունը հավասարասրուն չէ, ուստի այդ երկու ուղիները չեն կարող համընկնել, և շրջանագծի կենտրոնը՝ O-ն, պետք է գտնվի դրանց հատման կետում, այսինքն՝ M կետում։
Հետևաբար, խնդիրը լուծված է։
Հաջորդ խնդրում, որը առաջարկվել էր իններորդ դասարանցիներին Ա.Պ. Սավինի անվան մաթեմատիկական մենամարտերի մրցույթում, բարձրության և շառավղի համաչափության գաղափարը թաքցված էր մի փոքր ավելի խոր։
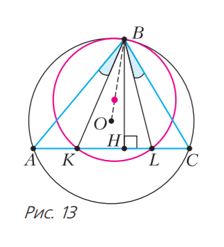
Խնդիր 5։ Տրված է սուրանկյոսւն եռանկյուն ABC։ կողմի վրա ընտրված է կամայական K կետ և այնպիսի L կետ, որ <ABK = <CBL (տես նկ․ 12)։ Ապացուցել, որ ABC և KBL եռանկյուններին արտագծած շրջանագծերի կենտրոնները գտնվում են միևնույն ուղու վրա։
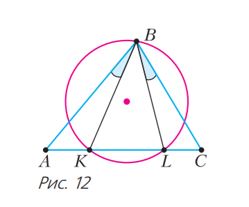
Լուծում։ Նկատենք, որ KBL և ABC եռանկյուններն ունեն AC կողմին տարված ընդհանուր բարձրություն՝ BH (տես նկ. 13)։
Բացի այդ, ∠ABK=∠CBL հավասարությունից հետևում է, որ այս եռանկյունները ունեն նաև ընդհանուր կիսորդ՝ տարված B գագաթից։
Այդ դեպքում՝ ըստ հետևանք 1-ի, ֆիքսված BO ճառագայթի վրա է գտնվում ոչ միայն եռանկյուն ABC-ին արտագծած շրջագծի կենտրոնը, այլ նաև եռանկյուն KBL-ին արտագծած շրջագծի կենտրոնը։
Հետևաբար, խնդիրը լուծված է։