Հեղինակ՝ Հուգո Շտայնհաուս
Այժմ ոչ այնքան հայտնի Ուայլդն ասել է, որ յուրաքանչյուրն իր մասնագիտությունը համարում է այն, ինչից ամենաքիչն է հասկանում։
Այս պարադոքսի իմաստը, հավանաբար, հանգում է հետևյալ պնդմանը․ ինչպես ձուկը, ամենայն հավանականությամբ, իրեն հաշիվ չի տալիս, թե ինչ է ջուրը և ինչ հատկություններ ունի (նույն ձևով իրավաբանը հազվադեպ է մտածում օրենքի էության մասին, իսկ կենսաբանին էլ չի անհանգստացնում կյանքի սահմանումը), այդպես էլ մաթեմատիկոսը հաճախ չի մտածում և խոսում այն մասին, թե ինչ է մաթեմատիկան:
Այսպիսի հարցեր միայն առաջանում են ոչ մաթեմատիկոսների հետ շփվելիս․ ինչպես ձուկը, հավանաբար, ջրից դուրս է միայն նկատում ջրի մակերևույթը, նրա սահմանները, յուրահատուկ հատկությունները։ Օրինակ՝ շատ դժվար է սահմանել, թե ինչ է քիմիան։ Ասել, որ այն ուսումնասիրում է նյութական մարմինների բաղադրությունը, պարզ է, որ բավարար չի լինի, քանի որ մինչ այդ անհրաժեշտ է սահմանել, թե ինչ ենք հասկանում «նյութ» ասելով (ընդ որում, հենց քիմիան և ֆիզիկան են մեզ հնարավորություն տալիս «նյութ» հասկացողությունը վերամշակելու)։
Չնայած, որ քիմիան արդեն բավականին զարգացած էր նախորդ հարյուրամյակում, նրա հիմունքների իմացությունը շատ հազվադեպ էր պրոֆեսիոնալ քիմիկոսների հետաքրքրության առարկա դառնում։ Այդպիսի հետազոտությունների խթան հանդիսացավ ժամանակակից ֆիզիկան։
Նույն ձևով մեր հարյուրամյակը խթան հանդիսացավ մաթեմատիկայի սկզբունքների ուսումնասիրության համար։ Այն եկել է տրամաբանությամբ հետաքրքրվող մաթեմատիկոսներից և մաթեմատիկական կրթություն ունեցող տրամաբաններից։ Նրանք էլ զբաղվեցին մաթեմատիկայի հիմունքներով և սահմանումով։ «Տրամաբան» բառն այստեղ ամենևին էլ չի նշանակում տրամաբանող մարդ, այլ նշանակում է մասնագետ, որ զբաղվում է մտածողության մեխանիզմներով, սահմանումներով, եզրահանգումներով և փաստարկներով։ Խոսքը զուտ ֆորմալ մեխանիզմի մասին է, որ թույլ է տալիս ինչ-որ դատողությունից բխեցնել մյուսները (անկախ դրանց էությունից)։
Բավականին վաղուց է հաստատվել, որ մաթեմատիկան տրամաբանորեն կապված դատողությունների հենց այդպիսի համակարգ է, և արդեն Լայբնիցը, 18-րդ դարի սկզբին սա հաշվի էր առել։
Ավելի դժվար է հանրամատչելի դասախոսությունում ներկայացնել, թե ինչ է մաթեմատիկան, ինչն է ընկած դրա առաջընթացի հիմքում:
Ազատ մաթեմատիկական դատողությունները ոչ միայն թույլ չեն տալիս պատշաճ պատկերացում կազմելու այս գիտության կարևորության և անսահմանության մասին, այլ նաև թույլ չեն տալիս պատշաճ գնահատելու սերունդների հսկայական ջանքերը՝ մաթեմատիկական խնդիրներ առաջադրելու և դրանց լուծման ճանապարհին հանդիպող դժվարությունները հաղթահարելու համար։
Մաթեմատիկան հանրամատչելի ներկայացնողի դերը լրացուցիչ բարդանում է նրանով, որ այս գիտությանը այնքան հազվադեպ է ուշադրություն հատկացվում սովորական դասախոսություններում, որ նույնիսկ մաթեմատիկայի մասին հանրամատչելի զրույցի տեխնիկան պատշաճ սահմանված չէ։
Մաթեմատիկան նման է աշտարակի, որի հիմքերը դրվել են շատ դարեր առաջ, և որի վերին հարկը դեռևս կառուցվում է։
Շինարարության ընդհանուր ընթացքը գնահատելու համար պետք է բազմաթիվ աստիճաններ ունեցող շատ թեք սանդուղքով բարձրանալ ամենավերևի հարկը: Ներկայացնողի դերն այն է, որ ունկնդրին վերելակով բարձրացնի ամենավերևը, որտեղից նա չի տեսնի ո՛չ միջանկյալ հարկերը, ո՛չ էլ դարերի ընթացքում զարդարված սենյակները, բայց կհամոզվի, որ կառույցը շատ բարձր է և շարունակում է բարձրանալ։
Մեկ նախադասությամբ սահմանելու փոխարեն, թե ինչ է մաթեմատիկան, մենք կփորձենք այն «ցույց տալ», ընդ որում ոչ միայն այն պատճառով, որ դժվար է ընդհանուր սահմանում տալը, այլ նաև այն պատճառով, ինչպես մեզ է թվում, երբեմն որպես մաթեմատիկա ընդունում են մի բան, ինչը մաթեմատիկա չէ։
Գոյութուն ունի որոշակի երգիծական տեսակետ մաթեմատիկայի հանդեպ, ավելի ճիշտ՝ նույնիսկ այդպիսի երկու տեսակետ։ Դրանց մասին կարելի է հաճախ լսել վագոնում կամ սրահում կամ կարդալ գրքերում և ամսագրերում։ Շատ զվարճասերներ անմիջական զրույցների ժամանակ կարող են ծիծաղելի բաներ պատմել մաթեմատիկայի մասին։ Օրինակ՝ ընդունված է համարել, որ մաթեմատիկոսները մարդիկ են, ում համար հաճույք է տասանիշ թիվը տասներկուանիշ թվով բանավոր բազմապատկելը, լոգարիթմների աղյուսակից էջեր հիշելը կամ պարզապես ոչ սովորական թվեր հավաքագրելը։
Բազմազանության համար կարելի է պատմել ճիշտ հակառակ պատմություններ այն մասին, որ մաթեմատիկոսները վատ են հաշվարկներ անում (օրինակ՝ մի խնդուկ այն մասին, թե ինչպես առաջին հանդիպած խանութպանը կարող է անհարմար դրության մեջ գցել մաթեմատիկոսին՝ բանավոր հաշվելով բարդ տոկոսներ, մինչ մաթեմատիկոսը կթերթի լոգարիթմական աղյուսակները, որպեսզի հաշվարկներում չսխալվի)։
Բնականաբար, իրական կյանքը բոլորովին չի համապատասխանում այս պատմություններին։
Մաթեմատիկոսները սովորաբար լավ «հաշվիչներ» կամ հաշվապահներ չեն, բայց նրանք ավելի վատ չեն հաշվում, քան միջնակարգ կրթություն ստացած մարդկանցից ցանկացածը։ Նրանք, որպես կանոն, չունեն հակումներ և մեծ փորձ հաշվողական աշխատանքներում։
Հաշվողական աշխատանքը (զուտ թվաբանական գործողությունները) ընդհանուր առմամբ շատ փոքր դեր է խաղում մաթեմատիկայում՝ անկախ նրանից, թե ինչ են մտածում այդ մասին ոչ կրթված մարդիկ: Ընդհակառակը, կիրառական մաթեմատիկայում (օրինակ՝ աստղագիտության վերաբերյալ խնդիրներում) հաշվողական աշխատանքները շատ են, և հենց աստղագետներն են օրինակը այն մարդկանց, որոնք մաթեմատիկայից ունեն ընդհանուր գիտելիքներ և կարող են շատ ավելի լավ հաշվարկներ կատարել, քան ամենաորակյալ հաշվապահները։ Աստղագիտությունը կարիք ունի մեծ թվով հաշվարկների ոչ միայն այն պատճառով, որ երկնային մարմինները գտնվում են մեծ հեռավորությունների վրա, այլ նաև, որ նրանց շարժումը Երկիր մոլորակի նկատմամբ շատ բարդ է։ Երկրի ամենամոտ արբանյակի՝ Լուսնի հետագծի որոշելը շատ ավելի հաշվարկ է պահանջում, քան ամենահեռավոր աստղերի հետագծերինը:
Սակայն երբեմն իրոք լինում են այնպիսի մարդիկ, որոնք կարողանում են շատ ավելի արագ կատարել բազմանիշ թվերով թվաբանական գործողությունները, քան հաշվիչ մեքենաները։ Այդպիսի բացառիկ մարդկանց մասին հաճախ են գրում հոգեբանական ամսագրերում, և ձեզանից շատերը հավանաբար լսել են Ինոդի, Դիոմանդի, Ռյուքլեի ազգանունները։ Այս մարդիկ սովորական իմաստով մաթեմատիկոսներ չեն, չնայած կարող էին և լինել (ինչպես վկայում է մաթեմատիկական գիտությունների դոկտոր Ռյուքլեի օրինակը)։
Ամենից հաճախ նրանք չունեն մաթեմատիկական կրթություն և հազվադեպ են օժտված լինում մաթեմատիկական ընդունակություններով։ Նրանցից մեկի հետ ինձ հաջողվեց երկար զրուցել, ես ապշած էի նրա՝ մաթեմատիկական կարողությունների բացարձակ բացակայությունից․ նա չէր հասկանում այնպիսի բաներ, որոնք հասանելի են միջնակարգ դպրոցի ավագ դասարանների սովորական կարողություններով օժտված գրեթե բոլոր աշակերտներին:
Հաշվի առնելով, որ մաթեմատիկոսները չեն զբաղվում հաշվարկներով, թեպետ անհրաժեշտությունից ելնելով պետք է զբաղվեն (երբեմն այն հնարամտության աղբյուր է)՝ տգետների շարքում առաջացավ երրորդ կեսլուրջ կատակը՝ կապված մաթեմատիկոսների աշխատանքի ծիծաղելի բացատրության հետ (իբր նրանք ապացուցում են, որ 2 x 2 = 5):
Այս թյուրամացությունների խորքային պատճառը մաթեմատիկական շարադրանքների ձևն է։
Նրանց տեքստերը անընդհատ զուգորդվում են բանաձևերով, որոնք երբեմն կարող են լցնել էջեր և կազմված են տառերից և անհասկանալի նշաններից։ Մաթեմատիկան շատերի համար առեղծվածային գիտություն է։ Ինչի՞ համար են այդ տարօրինակ նշանները և սիմվոլները։
Ակնհայտ է, որ այդ տառերից՝ մեծ ու փոքր, լատիներեն և հունարեն, պետք է բխի ինչ-որ նոր, թաքնված ճշմարտություն, բայց այն պետք է տարբերվի սովորական պնդումներից, ինչպիսիք են՝ 2 x 2 = 4 (մարդիկ սա վաղուց գիտեն առանց որևէ նշանների):
Այստեղից էլ միտք է ծագում, որ նման ջանքերն ու տեքստերը պետք է տանեն ինչ-որ պարադոքսի կամ անհնարինի, ինչպիսիք են կյանքի էլիքսիրը, փիլիսոփայական քարը կամ հավերժական շարժիչը, մի խոսքով՝ «2 x 2 = 5»:
Այն, որ միջին դպրոցում արդեն ուսումնասիրում են մաթեմատիկա, որտեղ կան a, b, c,…, x, y, z նշանները, չի փոխում այս տեսակետը, քանի որ աշակերտների մեծ մասը չի տեսնում այդ սիմվոլների իմաստը և նշանակությունը։ Մարդիկ չեն հասկանում այդ սիմվոլները, քանի որ գործնական կյանքում նրանք օգտագործում են ոչ թե տառեր, այլ կոնկրետ թվեր (2, 3, 5, 6.5 և այլն):
Բայց կան բացառություններ, օրինակ՝ եթե բանակի շտաբը նախատեսում է հարձակողական գործողություն և սպասում է ծանր զրահատեխնիկային (հայտնի է, որ դրանք անպայման կհասնեն, բայց հստակ հայտնի չէ, թե երբ), ապա կարելի է մանրամասն պլանավորել ամբողջ գործողությունը և հրամայել, որ հետևակային դիվիզիան հարձակվի x ժամին, դաշտային հրետանին սկսի գործել x ժամ 45 րոպեին, իսկ ծանր զրահատեխնիկան՝ x + 1 ժամին:
Նման հրաման կարելի է փոխանցել ստորադաս հրամանատարներին՝ չնշելով սիմվոլների կոնկրետ նշանակությունը, իսկ վերջիններս կարող են բանակի հրամանատարից պարզաբանումներ պահանջել հրամանի կատարման վերաբերյալ այնքան ժամանակ, քանի դեռ մի կարճ հաղորդագրություն չի ասել սիմվոլի արժեքը։ (x = օգոստոսի 31, 4 ։ 30):
Այս օրինակը ցույց է տալիս, որ որոշ դեպքերում սիմվոլն անհրաժեշտ է և այն չես կարող փոխարինել կոնկրետ թվով: Մաթեմատիկոսները հենց այդպես էլ օգտագործում են սիմվոլները. նրանք չեն գրում թվեր այնքան ժամանակ, քանի դեռ թվերը պարզապես ավելորդ մանրամասներ են, որոնք կապ չունեն հարցի էության հետ։ Ի՞նչ հետաքրքրություն են ներկայացնում այդ սիմվոլները կամ թվերը մեզ համար։ Դրանցից ոչ մեկի մասին առանձին ոչ մի հետաքրքիր բան չես կարող ասել, բայց դրանցից տարբեր ձևերով կազմված արտահայտությունների միջև երբեմն շատ զարմանալի և հետաքրքիր կախվածությունների հսկայական բազմազանություն է առաջանում:
Բազմաթիվ օրինակներից ընտրենք մեկը՝ վերցնենք կամայական a,b, c, d,e, f թվերը և կազմենք արտադրյալներ՝ axd, bxe, cxf, որոնք կարճ կգրենք այսպես՝ ad, be, cf:
Հետագայում կգտնենք դրանց գումարը՝ (𝑎𝑑+𝑏𝑒+𝑐𝑓), կբարձրացնենք քառակուսի՝ (𝑎𝑑+𝑏𝑒+𝑐𝑓)2, այդ ճանապարհով ստացված թիվը կնշանակենք l: Այժմ գրենք այդ վեց թվերի քառակուսիները՝ a,b,c, d, e, f, 𝑎2, 𝑏2, 𝑐2, 𝑑2, 𝑒2, 𝑓2, կազմենք դրանցից երկու գումար՝ 𝑎2+ 𝑏2+ 𝑐2, 𝑑2+ 𝑒2+ 𝑓2, բազմապատկենք (𝑎2+ 𝑏2+ 𝑐2)( 𝑑2+ 𝑒2+ 𝑓2) ։
Այս ճանապարհով ստացված թիվը նշանակենք m-ով։
Այսպիսով, այս թվերի վերաբերյալ մենք կարող ենք վստահ ասել, որ l թիվը միշտ (այսինքն՝ a, b, c, d, e, f ցանկացած արժեքի դեպքում) փոքր կամ հավասար կլինի m թվից: Օրինակ՝ (a = 1, b=2, c=1, d=3, e=4, f=1) ստանում ենք՝ 𝑎𝑑=3, 𝑏𝑒=8, 𝑐𝑓=1, 𝑎𝑑+𝑏𝑒+𝑐𝑓=12, (𝑎𝑑+𝑏𝑒+𝑐𝑓)2=144 այսինքն` l = 144. m թիվը գտնելու համար մենք հաշվում ենք պահանջվող արժեքները.
𝑎2 =1, 𝑏2=4, 𝑐2=1, 𝑑2 =9, 𝑒2 =16, 𝑓2 =1, 𝑎2+ 𝑏2+ 𝑐2= 6
𝑑2+ 𝑒2+ 𝑓2 =9+16+1=26
(𝑎2+ 𝑏2+ 𝑐2 ) (𝑑2+ 𝑒2+ 𝑓2 )=6∙26=156
Այսպիսով, m=156, պարզ է, որ մեծ է 144-ից։
Ստուգելու համար կարող ենք a, b, c, d, e, f-ի փոխարեն տեղադրել ցանկացած այլ արժեքներ, բայց վերը նշված պնդումը նորից ճիշտ կլինի։ Այս պնդումը մաթեմատիկորեն գրվում է հետևյալ տեսքով և կոչվում է Լագրանժի անհավասարություն․
(ad + Ье + сf)2 ≤(а2 + Ь2 + с2) (d2+ е2 + f2 )
Առանց տառային նշանակումներ օգտագործելու շատ դժվար կլիներ պնդումն արտահայտել և գրել։
Որպես երկրորդ օրինակ՝ դիտարկենք երկու տարբեր դրական թվեր՝ p և q։ Սկզբից p թիվը բաժանենք q-ի, հետո q-ն բաժանենք p-ի և գումարենք ստացված արդյունքները։
Կարելի է պնդել, որ ստացված գումարը միշտ մեծ կլինի 2-ից, ինչը համապատասխանում է հետևյալ տառային գրառմանը՝
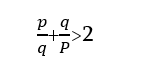
Այսպես, օրինակ՝ ունենք
և այլն, այսինքն` ստացված թիվը միշտ մեծ է 2-ից։
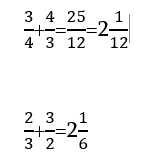
Մաթեմատիկայի խնդիրներից մեկը նմանատիպ պնդումներ ապացուցելն է։ Սակայն ապացույցը չի հիմնվում փորձերի վրա, և այն չի կարելի փոխարինել p-ի և q-ի փոխարեն նույնիսկ հազարավոր նոր արժեքների համար փորձերով։ Ապացույցը պահանջում է դուրս բերել
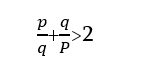
-ի ընդհանուր դեպքը՝ հիմնվելով թվերի սկզբունքային հատկությունների վրա։
Երբ հնարավոր է լինում ապացուցելը, ստացված դատողությունը անվանում են մաթեմատիկական պնդում, և այդ պահից սկսած գալիս է վստահությունը, որ ոչ մի փորձարկում չի կարող հերքել այդ դատողությունը։
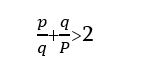
Այսպիսով, մաթեմատիկայի նպատակներից մեկն է նոր պնդումներ բացահայտելը և ապացուցելը։
Մաթեմատիկան, որը զբաղվում է հենց սրանով, կանվանենք տրամաբանական կամ «α» մաթեմատիկա։
Դպրոցը, ինչպես հայտնի է, քիչ է հետաքրքրվում «α» մաթեմատիկայով, քանի որ աշակերտներից չի պահանջում նոր պնդումներ բացահայտել, այլ հասնում է միայն նրան, որ արդեն հայտնի պնդումներից կարողանան ընտրել այն պնդումները, որոնք թույլ կտան լուծել կոնկրետ խնդիրը։
Մաթեմատիկան, որը զբաղվում է խնդիներ լուծելով, կանվանենք «β» մաթեմատիկա կամ հաշվողական մաթեմատիկա։ Առաջին հայացքից կարող է թվալ, որ Լագրանժի անհավասարումը մաթեմատիկական իմաստազուրկ հանելուկ (շարադա) է։ Այնուամենայնիվ այն նշանակություն ունի ոչ միայն «α» կամ «β» մաթեմատիկաների համար, այլև շատ հաճախ օգտագործում են օրինակ բնագետները, երբ ուզում են արտահայտել երկու երևույթների կախվածությունը միմյանցից։ l և m թվերը կարող են հավասար լինել, եթե a, b, c և d, e, f թվերի շարքերը համեմատական են (օրինակ՝ a=2d, b=2e, c=2f)։
Ենթադրենք, ժամը մեկ չափում ենք տվյալ տեղանքի մթնոլորտային ճնշումը և ջերմաստիճանը (համապատասխանաբար նշանակենք a, b, c –ով ճնշման արժեքները, իսկ d, e, f -ով՝ ջերմաստիճանի արժեքները)։ Այնուհետև, եթե ստացված արդյունքներով կազմենք l և m թվերը, նրանց հարաբերությունը թույլ կտա դատել այդ երկու մեծությունների փոխադարձ կախվածության աստիճանի մասին։
l=m հավասարությունը ցույց կտա ջերմաստիճանի ուժեղ կախվածությունը ճնշումից, l/m հարաբերության փոքր լինելը, օրինակ ½ դեպքում, ցույց կտա այդ մեծությունների թույլ կախվածությունը, իսկ l/m հարաբերության զրոյի ձգտելը ապացուցում է, որ հետազոտվող մեծությունները անկախ են։
l/m թիվը կոչվում է հարաբերակցության (կորելացիայի) գործակից։ Ելնելով այն փաստից, որ մաթեմատիկական պնդումները կարող են օգտագործվել նաև այլ գիտություններում, առաջացավ «γ» մաթեմատիկան, որին կոչում են կիրառական։ Ընդ որում, եթե իրոք ուզում ենք ուսումնասիրել դիտարկումների երկու հաջորդականություններ՝ օգտագործելով կորելացիայի գործակիցը, ապա պետք է սովորենք կատարել հաշվարկների մի ամբողջ շարք։ Թե ինչպես ավելի հեշտ և լավ կատարել ստանդարտ հաշվողական գործողություններ, սովորեցնում է գործնական մաթեմատիկան, որը կարելի է անվանել «δ» մաթեմատիկա։ Օրինակ՝ ճնշման կախվածությունը ջերմաստիճանից ուսումնասիրելու դեպքում շատ ավելի հարմար է մթնոլորտային ճնշումը հաշվել ոչ թե զրոյից, այլ, ասենք 700 մմ ս.ս.-ից. (այսինքն՝ 705 մմ ճնշումը համարենք 5 մմ և այլն, ինչը էապես կհեշտացնի հաշվարկները): Մոտավորապես այսպիսին են գործնական մաթեմատիկայի կանոնները։ Մաթեմատիկայի էությանը ոչ ամբողջական, միակողմանի հայացքը պայմանավորված է նրանով, որ մարդկանց ճնշող մեծամասնությունը գործ չի ունենում մաթեմատիկայի հետ՝ բացի «δ»-ից։ Կրթված մարդկանց մեծամասնությունը «β»-ից և «δ»-ից բացի այլ մաթեմատիկիայի չի հանդիպում: Այդ պատճառով էլ ինքներս մեզ հարց տանք՝ ի՞նչ նշանակություն ունեն կյանքում «α» և «γ» մաթեմատիկաները։ Այստեղ բավական է մեկ օրինակ բերել։ XVII դարում Դեկարտը ստեղծեց վերլուծական երկրաչափությունը, ինչը թույլ տվեց իր հետևորդներին զբաղվելու, այսպես կոչված, շոշափողի խնդրով, այսինքն՝ տրված կոր գծին շոշափող ուղիղ գծի դիրքը որոշելը։ Այդ խնդրից բխեց Լայբնիցի և Նյուտոնի դիֆֆերենցիալ և ինտեգրալ հաշվարկը, որը թույլլ տվեց Նյուտոնին ստուգել մարմինների փոխադարձ ձգողության իր տեսության կիրառելի լինելը մոլորակների շարժման դեպքում։ Այդ շարժման համապատասխանությունը տեսությանը ֆիզիկոսներին համոզեց նյուտոնյան մեխանիկայի սկզբունքների ճշմարտացիությունը, և այդ մեխանիկայի կիրառությունը երկրային ֆիզիկական երևույթների նկատմամբ հիմք հանդիսացավ ժամանակակից ֆիզիկայի համար։ Այս ամենը դարձավ ժամանակակից տեխնիկայի հիմքը, որը (հիմնականում հաղորդակցական միջոցների անասելի բարելավման և ձեռքի աշխատանքը մեքենաներով փոխարինելու շնորհիվ) հանգեցրեց նյութական մշակույթի փոփոխությանը, փոխեց բարիքների բաշխումը, ինչը արդյունքում հանգեցրեց սոցիալական շերտավորմանը, նոր դասակարգերի առաջացմանը, նոր քաղաքական համակարգերի, հայացքների և բարքերի ձևավորմանը։ Պատմաբանը այս դատողությունների համար մեզ կհանդիմանի և կասի, որ այսքան հեռու գնացող հետևանքների հանգեցրել է նոր մայրցամաքների հայտնաբերումը (օրինակ՝ վենետիկցիների աշխարհագրական հայտնագործությունները), բայց այդ բացահայտումները մեծ նշանակություն չէին ունենա առանց ծովագնացության մշակույթի էական առաջընթացի, ինչը անհնար կլիներ առանց աստղագիտության և օպտիկայի զարգացման, այսինքն՝ առանց գիտությունների, որոնք կապված են մաթեմատիկայի հետ։ Կհարցնեք, թե ինչպես է մաթեմատիկան կապված ֆիզիկայի հետ։ Ի՞նչ ընդհանուր բան կարող են ունենալ կանոնները, որոնց ենթարկվում են թվերը, և կանոնները, որոնց ենթարկվում է նյութը։ Այսպես, ֆիզիկայի օրենքները կապ են հաստատում որոշ մեծությունների միջև, որոնք կարող են դիտարկվել և չափվել։ Այդ մեծությունների չափումը տալիս է որոշակի թվեր, այսինքն, փաստորեն ստանում ենք թվերի միջև կախվածություն։ Մաթեմատիկան սովորեցնում է, թե այդ սկզբնական կախվածություններից ինչ կապեր են առաջանում թվերի միջև, և դրանով թույլ է տալիս ֆիզիկայի դիտարկված օրենքներից դուրս բերել (արդեն առանց դիտարկումների) նոր օրենքներ և կանխագուշակել նոր երևույթներ։ Դիտարկումը սովորեցնում է, որ եթե փակ անոթում փոխենք գազի ծավալը, օրինակ՝ մխոցով սեղմենք, ապա ճնշումը կփոխվի այնպես, որ ծավալի և ճնշման արտադրյալը կմնա հաստատուն։
Եթե մինչև փոխելը, ծավալը հավասար էր vo, իսկ ճնշումը՝ p0, իսկ փոփոխելուց հետո՝ համապատասխանաբար՝ v, р, ապա՝ vр = v0р0
Այս պնդումը կոչվում է Բոյլի օրենք։ Այս vр = v0р0 կախվածությունից կարելի է հաշվել, թե ինչ ճնշում է պետք գործադրել տրված գազը հեղուկ դարձնելու համար, եթե հայտնի է, թե քանի անգամ է հեղուկի խտությունը մեծ գազի խտությունից։ Իրականում գործը բարդանում է նրանով, որ տրված պրոցեսի վրա ազդում է նաև ջերմաստիճանը, բայց այդ ազդեցությունն էլ կարելի է մաթեմատիկորեն հաշվի առնել։ Այս vр = v0 р0 կախվածությունը մաթեմատիկական պնդում չէ (ինչպես վերը նշված Լագրանժի անհավասարումը), պարզապես ֆիզիկայի օրենք է՝ գրված մաթեմատիկական սիմվոլներով։ Մինչ այժմ մեր բերած բոլոր օրինակները ունեին այն թերությունը, որ թվաբանական չորս գործողություններից այն կողմ չեն անցել, իսկ թվաբանությունը մաթեմատիկայի ամենապարզ մասն է։
Սակայն ստիպված ենք դուրս գալ տարրական մաթեմատիկայի սահմաններից, արդեն առաջին հայացքից շատ պարզ թվացող խնդիրներ լուծելիս, օրինակ՝ շրջանագծի հատկությունները դիտարկելիս։ Ինչի՞ է հավասար շրջանագծի երկարությունը։
Դպրոցից մեզ հայտնի է, որ այն 3.1415926… անգամ մեծ է շրջանագծի տրամագծից, բայց այդ փաստն ինքնին հետաքրքիր չէ։ Այն ստուգելու համար անհրաժեշտ է չափել շրջանագծի երկարությունը, որը հնարավոր չէ իրականացնել փայտե կոշտ քանոնով, ինչը հանգեցնում է կոր գծերի երկարութունը հաշվելու խնդրին: Ակնհայտ է, որ կորի գծի աղեղը դեցիմետրերով չափելիս մեր սխալը ավելի փոքր կլինի, քան եթե չափենք մետրերով, իսկ ավելի լավ է չափել սանտիմետրերով և այլն: Սակայն, ինչպես գտնել իրական երկարությունը։
Կարելի է վերցնել շատ ավելի փոքր չափման միավորներ և ստանալ շատ ավելի մեծ թվեր (մետրերով), օրինակ՝ 1.9,1.99,1.999 ..․ Բայց դրանցից ոչ մեկը չի լինի աղեղի իսկական երկարության չափը, անվանենք այն ամբողջ թիվը, որն ավելի մեծ է ստացված յուրաքանչյուր թվից (օրինակ՝ 2):
Այս տեսակի սահմանումները վերաբերում են բարձրագույն մաթեմատիկային։
Այն սովորեցնում է, թե ինչպես գտնել և ինչպես հաշվել 3.1415926 թիվը՝ (π) Լուդոլֆովյան թիվը։ Օրինակ՝ Էյլերը առաջարկել է հետևյալ բանաձևը՝
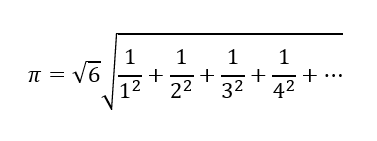
«α» մաթեմատիկայի համար առավել հետաքրքիր կլինի այն փաստը (ապացուցել է Լանդիմանը Մյունխենից), որ π թիվը երբեք չի կարող լինել ամբողջ գործակիցներով հավասարման լուծում։
Դրա համար էլ գրելով այսպիսի բարդ հավասարում, կարելի է նախօրոք ասել, որ π թիվը նրա լուծումը չէ։ 10х7 — 24х6 + 100х5 — 3х4 + 7х3 + 15x — 365 = 0
Այստեղից էլ բխում է, որ հնարավոր չէ կարկինի և քանոնի օգնությամբ ճշգրիտ չափել շրջանագծի երկարությունը կամ շրջանի մակերեսը, այսպես կոչված «շրջանի քառակուսացման անհնար լինելը»։ Նույնիսկ պարզագույն երևույթներն ունեն իրենց մաթեմատիկական կողմը, և ավելի խորը հետազոտումը հանգեցնում է դժվար և կարևոր խնդիրների։ Քարտեզագիրներին վաղուց հայտնի է, որ գնդի վրա քարտեզը ներկելու համար բավական է չորս գույն։
Այլ կերպ ասած, եթե պետք է, որ գլոբուսի վրա յուրաքանչյուր երկիր ունենա իր հարևան երկրներից (կամ ծովից, եթե երկիրը ծովամերձ է) տարբեր գույն, բավական է օգտագործել չորս գույն (ընդ որում, չի պահանջվում, որ այն երկրները, որոնք սահմանակցում են առանձին կետերով, ունենան տարբեր գույն)։ Մինչ այսօր ոչ մեկին չի հաջողվել ապացուցել այս պնդումը, բայց դրա փոխարեն ապացուցված է, որ տորի (փակ խողովակ) մակերևույթի վրա երկրների բաշխման դեպքում անհրաժեշտ է յոթից ոչ ավելի գույն։
Այստեղից միանգամից հարց է առաջանում գնդի և տորի սկզբունքային տարբերության մասին․
Առաջին հայացքից հարցը պարզամիտ է թվում, քանի որ նրանք ունեն բոլորովին տարբեր մակերևույթներ, և դժվար չէ տալ նրանց երկրաչափական նկարագրությունը, որը նույնպես տարբեր կլինի։
Բայց խոսքն այդ մասին չէ։ Չէ որ բոլորին հայտնի է, որ եթե խոսում ենք քարտեզի գունավորման մասին, կաևոր չէ՝ արդյոք գլոբուսը ճշգրիտ գունդ է կամ տափակեցված կամ որոշ տեղերում ծռված։ Այստեղ խոսքը գնում է ինչ-որ ուրիշ «ոչ ճշգրիտ ձևերի» և տարբերությունների մասին։
Օրինակ՝ վերցնենք շիշը։ Ինչ-որ ժամանակ այն եղել է ապակեգործարանի աշխատողի օդամուղ խողովակի ծայրից կախված տաք ապակու մեծ կաթիլ, որից նա կարող էր պատրաստել ինչպես ցմփոր շիշ, այնպես էլ՝ ծաղկաման։ Բայց առանց խողովակից կաթիլը պոկելու, նա չէր կարողանա պատրաստել երկու վզիկ ունեցող շիշ։ Նկարագրելու և ձևը որոշելու եղանակը, որի դեպքում նույնացվում է այն ամենը, ինչ ստացվում է միևնույն սկզբնական վիճակից «ձգելու» միջոցով, կոչվում է տոպոլոգիա։ Տոպոլոգիայիում հարթ շրջանը և շիշը նույն բաներն են։ Չէ որ շրջանից՝ նրա եզրերը ձգելու միջոցով կարելի է ստանալ ծաղկաման, իսկ ծաղմականից՝ վզիկը ձգելու միջոցով՝ շիշ։ Շիշը գնդից տարբերվում է նրանով, որ այն կարելի է կտրել՝ հատույթ տանելով բերանի մի կետից մինչև մյուսը, մինչդեռ գունդն այս եղանակով կտրել հնարավոր չէ։
Գունդը կտրելու համար անհրաժեշտ կլինի կտրվածքը սկսել և ավարտել նույն կետում, ինչը թույլ կտա երկու շիշ պատրաստել: Այսպիսի գործողությունը կոչվում է «փակ հատույթ», սակայն տորի վրա նրա իրականացումը տորը չի բաժանի երկու մասի։ Որպեսզի տորը կտրվի, անհրաժեշտ է կատարել երկու փակ հատում։ Ոմանց բավական է շարադրել ձևերի տեսության միայն հիմունքները, որպեսզի կարողանան ինքնուրույն զարգացնել և խորանալ խնդիրներում, իսկ ուրիշների մոտ հարց է առաջանում՝ ընդհանրապես ինչի՞ համար է տոպոլոգիան։ Միանգամից կարելի է նկատել, որ տարբեր տոպոլոգիական ձևեր սկզբունքորեն տարբերվում են նաև ֆիզիկայի տեսանկյունից։ Այս տարբերությունը քանակական չէ, ակնհայտ է, օրինակ, գնդի մեջ հեղուկը չի կարող գտնվել, առանց անընդհատությունը խզելու, այնպիսի վիճակում, որ նրա բոլոր մասնիկները գտնվեն մշտապես շարժման մեջ, մինչդեռ տորում հնարավոր է նման շրջանառություն։ Հոլանդացի մաթեմատիկոս Բրաուերն ապացուցել է, եթե գնդի մակերևույթով, առանց անընդհատությունը խզելու վազում են մասնիկներ, ապա միշտ դրանցից առնվազն մեկը գտնվում է դադարի վիճակում։
Հիդրոդինամիկայի և էլեկտրականության մասին գիտության համար այս դատողությունները գործնական մեծ նշանակություն ունեն, հատկապես, երբ էլեկտրական ցանցում հոսանքի բաշխումը կախված է դրա տոպոլոգիայից, քանի որ մինչ այժմ ցանցի օպտիմալ չափերը որոշելը բախվում է ոչ այնքան հաշվողական դժվարությունների, որքան զուտ մաթեմատիկական։
Քարտեզագրության վերաբերյալ այլ տեսանկյունից մտորումները բերում են մաթեմատիկական հետաքրքիր տեսությունների։ Հնարավո՞ր է արդյոք որոշակի երկրի համար այնպես գծել քարտեզ, որ երկրի սահմանը շրջանագծի տեսք ունենա։ Ենթադրենք, որ երկիրը պատկերված է հարթության վրա, և ցանկանում ենք քարտեզն այնպես կազմել, որ քարտեզի վրա և իրականում հեռավորությունների հարաբերությունը (մասշտաբը) կախված չլինի ուղղությունից (և հետևաբար, մասշտաբի փոփոխությունը հյուսիս-հարավ և արևելք-արևմուտք ուղղություններով նույնը լինի), բայց միևնույն ժամանակ թույլատրվի, որ այս հարաբերությունը քարտեզի տարբեր կետերում տարբեր լինի։
Այս դեպքում փոքր տարածքները դեֆորմացիայի չեն ենթարկվի, բայց ամբողջ քարտեզը կփոխի իր իրական ձևը, իսկ մենք ուզում էինք, որ երկրի սահմանը քարտեզի վրա շրջանագծի տեսք ունենա: Այս խնդիրը ձևակերպել և լուծել է տոպոլոգիայի ստեղծող Բերնհարդ Ռիմանը, որի ծննդյան հարյուրամյակը վերջերս է նշվել։
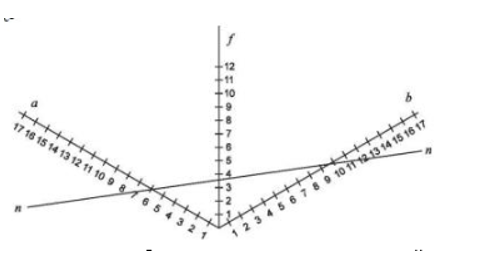
Հաջորդ սերնդի բեռլինցի գիտնական Գ.Ա.Շվարցը հաշվել է, թե ինչ տեսք կունենա քառակուսու շրջանաձև քարտեզը։
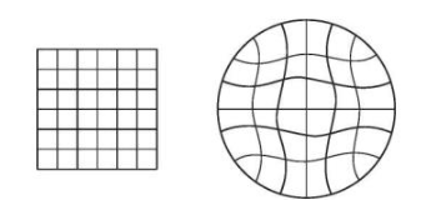
Նկարը ցույց է տալիս, թե շրջանաձև քարտեզի վրա ինչպիսի տեսք կունենան
քառակուսաձև երկրի զուգահեռներն ու միջօրեականները:
Եթե Ռիմանի թեորեմը վերաբերում է տրամաբանական մաթեմատիկային, ապա Շվարցի հաշվարկները վերաբերում են «β» մաթեմատիկային:
Եվ նորից, առաջին հայացքից կարող է թվալ, որ քառակուսաձև երկրների շրջանաձև քարտեզները կազմելը ժամանակի և էներգիայի վատնում է։
Մինչդեռ պարզվեց, որ եթե հարթության վրա գծենք հեղուկի հոսքի գծերը (ոչ մածուցիկ և չսեղմվող), այնուհետև կազմենք այդ գծերի քարտեզն այնպես, որ փոքր տարածքները դեֆորմացիայի չենթարկվեն, ապա քարտեզի վրա այդ գծերի պատկերները կրկին կլինեն գծեր, որոնց երկայնքով նշված պայմաններում կարող է հեղուկը հոսել:
Սա հենց կիրառական մաթեմատիկան է։
Վերը նշված ձևափոխությունները գործնականում օգտագործելու համար Կիրխհոֆը և Ռելեյը առաջարկել են մեթոդներ, որոնք պարզվեց, որ օգտակար են ժամանակակից օդանավաշինության համար և թույլ տվեցին նկարագրել ինքնաթիռի թևի շրջակա անցումը օդի հոսանքում։
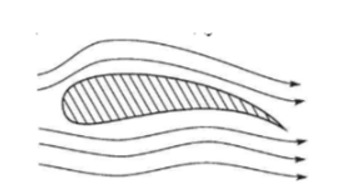
Այդ խնդիրը լուծելու համար անհրաժեշտ է նկարում պատկերված լայնական հատույթը փոխարինել շրջանով, այլ կերպ ասած՝ գտնել հոսքի գծերն այն դեպքի համար, երբ օդը բախվում է շրջանաձև հատույթով գերանի։ Այս դեպքի համար հաշվարկները շատ ավելի հեշտ է կատարելը, քան սովորական, բավականին բարդ կառուցվածք ունեցող թևի համար հոսքի գծերը որոշելը։ Նկարելով գերանին հանդիպող օդի հոսքի գծերը՝ կարող ենք ստանալ թևի հատույթի ետևում գտնվող հարթ տիրույթի քարտեզը (չընդգծված հատվածում), այնպես որ այդ տիրույթի սահմանը, որ որոշվում է թևի լայնակի հատույթով, քարտեզի վրա երևա որրպես շրջան։
Քարտեզի վրա նախկինում պատկերված օդի հոսքի գծերը իրական գծերի պատկերներն են, որոնք այժմ (իմանալով տիրույթի և քարտեզի միջև կապը) կարելի է գծել թևից դուրս գտնվող տիրույթում:
Այստեղ մենք ունենք, ինչպես ամբողջ աէրոդինամիկայում, կիրառական մաթեմատիկայի օրինակ, իսկ եթե տրված թևի համար իրականում որոշեինք օդի հոսքի գծերը և հետո հաշվարկեինք նրա ճնշման ուժը, ապա սա կլիներ գործնական մաթեմատիկայի հիանալի օրինակ:
Այս ամենն արդեն վերաբերում է բարձրագույն մաթեմատիկային։ Կիրառական մաթեմատիկայի ուսանելի օրինակ է երկրաչափական օպտիկան։ Փորձը ցույց է տալիս, որ յուրաքանչյուր օպտիկական սարքում լույսի ճառագայթները տարածվում են այնպես, որ մի կետից մյուսը հասնելու ժամանակը լինի նվազագույնը։ Այս փաստի հիման վրա կարելի է կիրառել երկրաչափությունը՝ օպտիկական սարքեր պատրաստելու և այդ սարքերում լույսի ճառագայթների տարածման կանոնները կանխատեսելու համար։ Նույնիսկ կարելի է նախօրոք որոշել, թե ինչպես պետք է հարթեցնել ապակիները և հայելիները՝ ցանկալի արդյունք ստանալու համար: Ոսպնյակի համար (f ֆոկուսային (կիզակետային) երկարություն ունեցող) երկրաչափական օպտիկան թույլ է տալիս ստանալ հետևյալ պարզ բանաձևը.
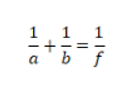
որտեղ a-ն ոսպնյակի հեռավորությունն է առարկայից, իսկ b- ն հեռավորությունն է պատկերից։ Այս բանաձևը շատ պարզ է և թույլ է տալիս հեշտությամբ գտնել f-ը՝ իմանալով a-ի և b-ի արժեքներից:
Սակայն, եթե ոսպնյակներ արտադրող գործարանում ինչ-որ մեկին անհրաժեշտ է մի քանի տասնյակ անգամ նման հաշվարկներ կատարել, ապա նա կարող է կիրառել կիրառական մաթեմատիկայի մեթոդները։ Հարցն այն է, որ f, a և b երեք մեծություններից ցանկացածը (երկու հայտնիների դեպքում) կարելի է գտնել առանց հաշվարկներ կատարելու՝ օգտագործելով երեք պարզ սանդղակներ, որոնք գտնվում են միմյանց նկատմամբ 60° անկյան տակ: Եթե նման սանդղակներին (ինչպես ցույց է տրված նկարում) ամրացնեք երկու տրված կետերով անցնող թել, ապա տրված a և b (կամ f) թվերից անմիջապես կարելի է որոշել f-ը (կամ համապատասխանաբար՝ b):
Նմանատիպ գրաֆիկական հնարքների հեղինակ է համարվում ժամանակակից ֆրանսիացի մաթեմատիկոս դ’Օկանը։ Մաթեմատիկական մտածողության մի քանի նման օրինակները բավական են ամենաընդհանուր գծերով ցույց տալու համար, թե ինչ է մաթեմատիկան։
Նրանցում նաև թաքնված է այն հարցի պատասխանների մի մասը, թե արդյո՞ք մաթեմատիկան զարգանում է, և եթե այո, ապա ինչի՞ վրա է հիմնված նրա առաջընթացը։
Վերադառնալով «2 x 2 = 5» կատակին, որ մաթեմատիկոսները ապացուցում են նման անհեթեթություններ՝ կարելի է ասել, որ սկզբնաղբյուրը շատ տարածված հետևյալ կարծիքն է՝ գիտությունը, որտեղ չկան տարաձայնություններ, չի կարող զարգանալ: Մաթեմատիկայի օրենքներն ու պնդումները հաստատվել են հազարավոր տարիների ընթացքում (իսկապես, դժվար է վիճարկելը, որ թվաբանության օրենքները հաստատվել են շատ դարեր առաջ), բայց բանավեճերի բացակայության դեպքում չկան գիտական վիճաբանություններ և վիճելի հարցեր, իսկ առանց դրանց գիտությունը նյութ չունի ուսումնասիրելու և զարգացման համար ներքին խթանիչներ չկան։ Իրականում այս կարծիքը սխալ է, քանի որ մաթեմատիկայում կա որոշակի հստակ սահման՝ հայտնիի և անհայտի միջև։ Օրինակ՝ հայտնի է, որ թիվը պարզ թիվ չէ (չբաժանվող), քանի որ կարելի է ապացուցել, որ այն առանց մնացորդի բաժանվում է 3-ի։ Միևնույն ժամանակ հայտնի չէ՝ թիվը բաժանվում է որևէ այլ թվի, թե ոչ։ Եթե վաղն ինչ-որ մեկին հաջողվի ապացուցել, որ այս թիվը բաժանվում է (օրինակ՝ 257-ի), նա թվաբանության մեջ շրջադարձային հեղափոխություն արած կլինի։ Բայց ոչ այսօր, ոչ էլ վաղը քննարկում չի լինի, թե արդյոք պարզ է (բաժանվող է), թե ոչ։ Այսօր մաթեմատիկոսներից ոչ մեկը չի կարող ասել՝ այդ թիվը բաժանվում է ինչ-որ թվի կամ էլ ասել հակառակը (նման կարծիքը նա ստիպված կլիներ անվանել ոչ թե գիտական թեզ, այլ ապացույց չունեցող ենթադրություն)։
Այդ դեպքում որտեղի՞ց է գալիս բանավեճի անհրաժեշտության մասին համառ կարծիքը։ Դրա աղբյուրը բնական գիտություններն են, որտեղ աշխատում են փորձարարական տվյալների հետ։
Լույսի տարածման ուղղագիծ լինելը ապացուցելու համար (երկու կետերի միջև ցանկացած անցման դեպքում) տարբեր պայմաններում հազարավոր փորձեր են արվել, որոնք միշտ նույն՝ դրական արդյունքն են տվել։ Բայց այդ ընթացքում չեն դիտվել որոշ այլ փաստեր (օրինակ, ինտերֆերենցիոն շերտերի առաջացումը /возникновение интерференционных полос/), որոնց գրանցման համար պահանջվում էին ավելի կատարելագործված գործիքներ և ավելի ճշգրիտ դիտարկումներ, ինչը հնարավոր դարձավ միայն նոր ժամանակներում՝ Նյուտոնից հետո։ Դրանից հետո փաստերը մեկը մյուսի հետևից դրվեցին կշեռքի հակառակ նժարին, և պարզվեց, որ լույսի ճառագայթը որոշակի պայմաններում կարող է կորանալ։ Ֆիզիկայի պատմության մեջ կար մի ժամանակ, երբ նման փաստերը քիչ էին, այդ ժամանակ, բնականաբար, առաջացավ և հնարավոր եղավ բանավեճը (լույսի ուղղագիծ տարածման կողմնակիցները կասկածում էին նոր դիտարկումների ճշմարտության վրա, այլ կերպ էին բացատրում շերտերի հայտնվելը և այլն), բայց, ի վերջո, բացասական արդյունքով փորձերի թիվը այնքան մեծ դարձավ, որ կշեռքի նժարը թեքվեց։ Մաթեմատիկայում նման բան չի կարող լինել։ Այստեղ փաստեր չեն կուտակվում, այստեղ բնական ինդուկցիա չկա։ Բավական է մեկ փաստարկ, որ պնդումը ճիշտ լինի, իսկ եթե փաստարկները բավարար չեն, ապա պնդումը պաշտպանելու հազարավոր փորձերը ոչինչ չեն նշանակում։ Եթե ինչ-որ մեկը փորձի թիվը բաժանել 2-ից 10000 թվերի վրա և ապացուցի, որ դրանցից ոչ մեկի վրա առանց մնացորդի չի բաժանվում, դա դեռ բավական չէ պնդելու համար, որ թիվը պարզ է, այսինքն՝ որ ոչ մի թվի վրա չի բաժանվում։ Թվաբանության ոլորտում առաջընթացի մասին չխոսեցի, քանի որ այդ հարցը մանրամասն ներկայացված է պրոֆ. Ռուզևիչի հատուկ դասախոսություններում։ Ինչ վերաբերում է հանրահաշվական հավասարումներին, ապա այստեղ 19-րդ դարի սկզբին ակնառու հաջողության են հասել Ռուֆինին, Աբելը և Գալուան։ Նրանք ապացուցել են, որ 5-րդ կարգի ընդհանուր տեսքի հավասարումը չի կարող լուծվել (ինչպես բնորոշ է ավելի ցածր կարգի հավասարումներին) նույնիսկ թվաբանական չորս գործողություններ և արմատ հանելու գործողություն պարունակող բանաձևերի տեսքով։ Այստեղ մի քանի խոսք պետք է ասել ժխտողական պնդումների դերի և բնույթի մասին։ Երբ անգետ մարդն իմանում է, որ կամայական անկյունը երեք հավասար մասի բաժանելու համար չկա կառուցման ձև, նրա մոտ սկզբունքային կասկածներ են առաջանում։ Օրինակ՝ նա կարող է հիշեցնել այն մասին, որ մեխանիկական միջոցներով թռիչքի անհնար լինելը բազմիցս ապացուցվել էր շատ լուրջ գիտնականների կողմից, մինչև որ այդ փաստարկների հետ չհամաձայնող գյուտարարը օդ բարձրացավ առաջին սավառնակով։ Բայց այսպիսի անալոգիան լրիվ անտեղի է, քանի որ (ինչպես հենց վերևում ասացի) ֆիզիկայում պնդումները հիմնված են մակածական եզրակացությունների վրա, որոնք կարող են հերքվել նոր փաստերով և գործոններով:
Ավիացիայում նոր գործոնը բենզինով թեթև շարժիչն էր։ Իսկ անկյունը երեք հավասար մասի բաժանելու անհնարին լինելու պնդումը Էվկլիդեսյան երկրաչափության աքսիոմների տրամաբանական հետևանք է։ Իհարկե, այն վերաբերում է կարկինով և քանոնով կառուցմանը կամ նույնիսկ ցանկացած այլ գործիքով, որոնց հատկությունները սահմանափակ են էվկլիդեսյան աքսիոմներով։ Ֆիզիկայում կարող է առաջանալ նոր խնդիրների մի ամբողջ դաս։
Օճառի փրփուրի մեջ ընկղմելով օղակաձև ծայրով մետաղալար՝ մենք ստանում ենք օճառե թաղանթ։ Ֆիզիկան պնդում է, որ օղակի վրա առաջացած թաղանթն ունի հնարավոր նվազագույն մակերես։ Այս երևույթը մաթեմատիկորեն նկարագրելու և նվազագոււյն մակերեսով մակերևույթ առաջանալը հիմնավորելու ցանկությունը հանգեցնում է «մասնակի ածանցյալներով դիֆֆերենցիալ հավասարումների», որը մեծ հետաքրքրություն է ներկայացնում մաթեմատիկական ֆիզիկայի համար։ Այս «նվազագույն» մակերևույթներով հետաքրքրվել են արդեն հիշատակված Ռիմանը և Շվարցը, ինչպես նաև նրանց շատ հետևորդներ (մինչև մեր օրերը), բայց նրանցից ոչ մեկը չի կարողացել ապացուցել նվազագույն մակերեսի առկայությունը բոլոր ձևերի համար։ Սկզբում նման կասկածը անհեթեթ է թվում, նախ՝ գոյություն ունի նվազագույն մակերես (քանի որ այն իրականում ձևավորվում է օճառի թաղանթով), և երկրորդ՝ նույն եզրագծի վրա ձգված բոլոր մակերևույթներից մեկը պետք է լինի նվազագույնը։
Ժամանակակից մաթեմատիկայի համար երկու փաստարկներն էլ բավարար չեն։ Ֆիզիկական փորձի վրա հիմնված ապացույցը վիճելի է և ենթակա է քննադատության։ Բոլոր մակերևույթների մեջ նվազագույնը գոյություն ունենալու փաստարկը ունի թաքնված սխալ (ինչը դեռ 19-րդ դարի 70-ականներին նշել է Վայերշտրասը), կապված այն բանի հետ, որ տրված թվերի բազմության մեջ միշտ չէ, որ կա ամենափոքրը։ Oրինակ՝ A և B կետերը միացնող կորերի մեջ չկա ամենակարճը, քան որ այդ կետերի միջև ամենակարճ հեռավորությունը АВ հատվածն է, որը չի պատկանում կորերին։ Այդ պատճառով էլ ժամանակակից մաթեմատիկան շատ դեպքերում փորձում է սկզբում ապացուցել լուծման գոյությունը և միայն դրանից հետո է անցնում լուծումը հաշվելուն։
Երբեմն պարզվում է, որ լուծումը գոյություն չունի, և ոչ այն պատճառով, որ չի կարող գոյություն ունենալ, այլ պարզապես, մենք չենք կարողանում այն գտնել։ Առանց համակարգված, երկար տարիների ուսուցման՝ դժվար է խորանալ խնդիրների և լուծումների այս անտառում, բայց կարող ենք հույս ունենալ, որ վերը նշված դատողությունները կհեշտացնեն հասկանալը, թե ինչի վրա է հիմնված մաթեմատիկական այն մեթոդը, որը (լինելով լրիվ տրամաբանական) գերիշխում է հասկացությունների, թեորեմների և խնդիրների անսահման բազմազանության տրամաբանության վրա։

