https:sumplete.com կայքում յուրաքանչյուրը կարող է խաղալ արհեստական բանականության կողմից հորինված և ծրագրավորված խաղը։
Ահա՛ խաղի կանոնները․
Որոշակի չափսերով տախտակի վրա, օրինակ՝ 3 x 3, գրված են թվեր։ Այդ թվերից մի քանիսը պետք է խաչով նշել այնպես, որ մնացած թվերի գումարը յուրաքանչյուր սյունակով, յուրաքանչյուր տողով համընկնի տախտակից դուրս գրված թվերի հետ։ Դիտարկենք նկարում բերված խաղը և փորձենք խաղալ։ Առաջին սյունակով և երկրորդ տողով թվերի գումարներն արդեն համըկնում են, այստեղ ոչինչ պետք չէ անել։ Նայենք երկրորդ սյունը։ Երկրորդ տողից պետք է մնա ութը, որպեսզի կարողանանք 12 ստանալ, խաչով կնշենք 7-ը։
Երրորդ սյունակում թվերի գումարը պետք է լինի 3, ուրեմն երկրորդ տողի 3-ը պետք է մնա։ Տե՛ս նկարը․
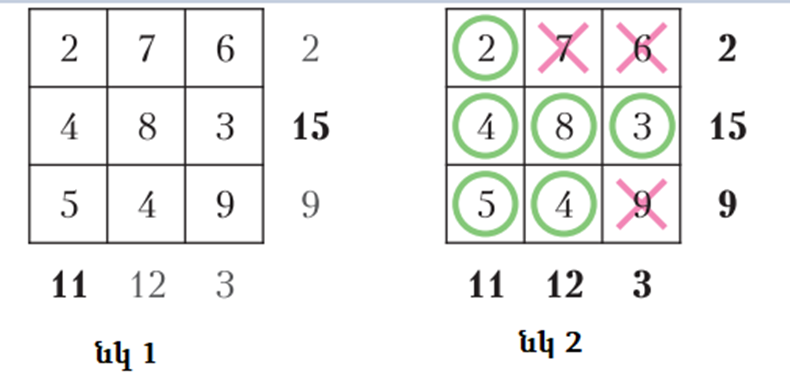
Փորձենք նայել արհեստական բանականության տեսանկյունից և հասկանալ, թե ինչպես են թվերն ի հայտ գալիս տախտակի վրա, և գումարները՝ տախտակի կողքերին։ Պարզ է, որ թվերի և գումարների ոչ բոլոր հավաքածուների դեպքում խնդիրը լուծում կունենա։ Օրինակ, եթե պահանջվող գումարներից մեկը ավելի մեծ լինի, քան տախտակի վրա եղած բոլոր թվերի գումարը, պարզ է, որ խաղը լուծում չի ունենա։ Բնական է ենթադրել, որ տախտակի վրա թվերը ի հայտ են գալիս պատահականորեն, իսկ հետո պատահական ձևով ընտրվում է «լուծումը» , և դրանով էլ որոշվում է գումարը։ Այս տարբերակն ամենահեշտն է (գոնե այդպես է թվում մարդու տեսանկյունից)։
Հարց է առաջանում՝ ինչ անել, եթե գոյություն ունենա համակարգչի լուծումից տարբերվող մեկ այլ լուծում։
Փորձենք հասկանալ՝ գոյություն ունե՞ն խելամիտ սահմանափակումներ սկզբնական տվյալների վրա, որպեսզի լուծումը միակը լինի։ Սկզբում դիտարկենք մի քիչ ավելի պարզ խնդիր։ Ենթադրենք ունենք ինչ- որ չափսերով տախտակ, որի յուրաքանչյուր տողի, սյան կողքին գրված է թիվ։
Մի քանի վանդակ անհրաժեշտ է ներկել այնպես, որ սյուների և տողերի ներկված վանդակների քանակները համընկնեն համապատասխան թվերի հետ։ Ըստ էության՝ սա նույն խնդիրն է, միայն թե հիմա ամեն վանդակում գրված է մեկ թիվը։
Պարզվում է, որ այս մասնավոր դեպքը լավ ուսումնասիրված է։
Կա լուծման գոյության չափանիշ, լուծման միակության չափանիշ և լուծումը գտնելու ալգորիթմ։ Սկսենք լուծման գոյությունից։ Դիցուք, պահանջվող գումարները տողերով վերևից ներքև r1, r2, r3, r4,….rm են, իսկ սյունակներով ձախից աջ՝ s1, s2, s3, s,….. s n :
Ներկենք առաջին տողում ձախ կողմի r1 վանդակը, երկրորդ տողում՝ ձախ կողմի r2 վանդակը, և այդպես շարունակ։ Ներկելու այս տարբերակը կանվանենք առավելագույն։
Առավելագույն ներկելու դեպքում յուրաքանչյուր սյան համար հաշվենք ներկված վանդակների քանակը, կստանանք որոշակի c1, c2, c3, ……cn թվեր։
Որպեսզի լուծումը գոյություն ունենա, անհրաժեշտ է և բավարար, որ տեղի ունենան այս անհավասարություննները՝
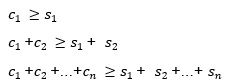
և այս հավասարությունը՝
r1+ r2+r3+….+ rm = s1+s2+s3….+sn :
Առաջադրանք 1. Ապացուցե՛ք, որ վերջին հավասարությունը հանդիսանում է անհրաժեշտ, բայց ոչ բավարար պայման լուծման գոյության համար։
Նայենք նկար 3-ի օրինակը։
Այստեղ r1=2, r2 =3, r3= 2 , s1 =2, s2=1, s3=2, s4=2 և r1 + r2 + r3 = s1 + s2 + s3 + s4 ։
Առավելագույնը կներկենք, (տե՛ս նկար 4) և կստացվի c1=3, c2=3, c3=1, c4=0 :
Այսպիսով՝ c1=3 ≥ 2=s1
c1+c2=3+3=6≥ 3=2+1=s1+s2
c1+c2+c3=3+3+1=7≥ 5=2+1+2=s1+s2+s3
և վերջապես՝
c1+c2+c3+c4=3+3+1+0=7 ≥ 7=2+1+2+2= s1+s2+s3+s4 :
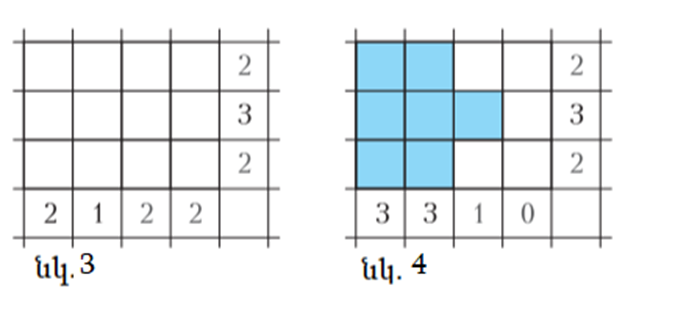
Այսինքն՝ լուծում պետք է գոյություն ունենա, այն ներկայացված է նկար 5-ում։
Հարց է առաջանում է` այս դեպքի համար լուծումը միա՞կն է։ Դժվա չէ կռահել, որ ոչ։
Օրինակ՝ կարող ենք տրված լուծման վերևի աջ քառակուսին 2×2 «շրջել», այսինքն` ներկել քառակուսու կարծես մյուս անկյունագիծը։
Պարզ է, որ այս դեպքում մենք կստանանք այլ լուծում։
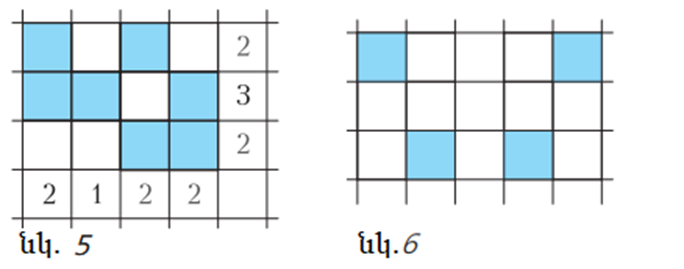
Իրականում նման «շախմատային քառյակների» առաջացումը ուղղանկյունների գագաթներում, որոնց կողմերը զուգահեռ են տախտակի գծերին, ինչպես նկար 6-ում է, միակ խոչընդոտն է լուծման միակության համար։
Ստացվում է, որ եթե ինչ-որ ճանապարհով ներկենք այնպես, որ չլինեն «շախմատային քառյակներ», ապա լուծումը կլինի տրված խնդրի համար միակը։
Թվում է, եթե գտնենք ներկելու ընդհանուր ալգորիթմ, ապա խնդիրն ամբողջությամբ լուծված կլինի․ սկզբում ստուգում ենք լուծման գոյության պայմանը, հետո այն կառուցում ենք ալգորիթմին համաձայն, իսկ հետո ստուգում ենք ցանցին զուգահեռ կողմերով ուղղանկյունների բոլոր գագաթների ներկված լինելը՝ լուծման միակությունը պարզելու համար։
Ալգորիթմ իրոք գոյություն ունի։ Սակայն այն բոլորովին էլ հեշտ չէ, և այստեղ չենք ներկայացնի։ Կբավարարվենք նրանով, որ այն գոյություն ունի և որոշ իմաստով գործում է «արագ»։
Խնդիրը, որը նոր դիտարկեցինք, առաջանում է դիսկրետ տոմոգրաֆիայում, որը կիրառվում է պատկերների մշակման, բժշկության և նույնիսկ տեղեկատվության անվտանգության հարցերում։
Խնդիրն ունի բավականին բնական ծագում․ փաստորեն խոսքը «ռենտգենյան ճառագայթների» մասին է, որոնք անցնում են որևէ օբյեկտի միջով, և ելքում ստացվում են միայն որոշ պրոյեկցիաներ, իսկ անհրաժեշտ է վերականգնել հենց օբյեկտի կառուցվածքը։
Առաջադրանք 2
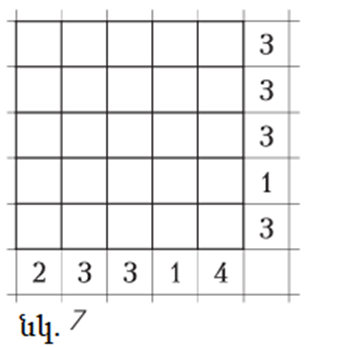
Գոյություն ունի՞ և միա՞կն է (գոյություն ունենալու դեպքում) դիսկրետ տոմոգրաֆիայի խնդրի լուծումը, որը պատկերված է նկար 7-ում։
Բայց վերադառնանք արհեստական բանականության կողմից առաջարկված խնդրին։ Գոյություն ունի՞ լուծման ալգորիթմ։ Ալգորիթմ, իհարկե, գոյություն ունի, կարելի է պարզապես ստուգել բոլոր հնարավոր տարբերակները։ Մեզ ավելի շատ հետաքրքրում է՝ գոյություն ունե՞ն լուծման «արագ» ալգորիթմներ։
Բանն այն է, որ գոյություն ունեն խնդիրներ, որոնք կարելի է «արագ» լուծել․ այդպիսի խնդիրները համարվում են P դասի։ Կան նաև խնդիրներ, որոնց լուծումները կարելի է «արագ» ստուգել․ դրանք պատկանում են NP դասին։ Պարզ է, որ եթե խնդիրը կարելի է «արագ» լուծել, ապա լուծումը կարելի է նաև «արագ» ստուգել՝ պարզապես դիտարկելով «արագ» գտնված լուծումը։ Այդ պատճառով, P դասին պատկանող յուրաքանչյուր խնդիր պատկանում է նաև NP դասին։
Սակայն, մինչև օրս հայտնի չէ՝ արդյոք ճիշտ է հակառակ պնդումը, այսինքն՝ յուրաքանչյուր NP դասի խնդիր պատկանո՞ւմ է P դասին։ Մարդկանց մեծամասնությունը կարծում է, որ NP- ում կան բավականին բարդ խնդիրներ, որոնք հնարավոր չէ «արագ» լուծել։
Ալգորիթմների տեսությունում ներկայացվում է մաթեմատիկական խիստ սահմանում ալգորիթմի «արագության» համար, սակայն մեզ համար ինտուիտիվ հասկանալն էլ բավական է։ Որպեսզի մի փոքր ավելի պարզ լինի, թե ինչ խնդիրների մասին է խոսքը, դիտարկենք մի քանի օրինակ։
Ենթադրենք տրված են երկու ամբողջ թվեր։ Անհրաժեշտ է գտնել դրանց ամենամեծ ընդհանուր բաժանարարը։ Կարող ենք օգտվել էվկլիդեսի ալգորիթմից։ Ամեն քայլին թվերից մեծը փոխարինում ենք այդ երկու թվերի տարբերությամբ։ Երբ թվերը համընկնում են, դադար ենք տալիս։ Ստացված թիվը կլինի այդ երկու թվերի ամենամեծ ընդհանուր բաժանարարը։ Այս խնդիրը պատկանում է P դասին։
Նայենք մեկ այլ օրինակ։ Ենթադրենք ունենք ամբողջ թվերի M մուլտիբազմություն (բազմություն, որի տարրերը կարող են կրկնվել) և ինչ-որ S թիվ։ Անհրաժեշտ է ստուգել՝ արդյոք M-ում գոյություն ունի մի ենթաբազմություն, որի տարրերի գումարը S է։ Դեռ հայտնի չեն այս խնդրի լուծման «արագ» ալգորիթմներ։ Այսպիսով, հայտնի չէ՝ պատկանում է արդյոք այս խնդիրը P դասին։ Բայց մենք կարող ենք հստակ ասել, որ այն պատկանում է NP դասին։ Եթե մեզ տան որոշ թվերի բազմություն՝ բավական է պարզապես ստուգել, որ մեզ չեն խաբել, այսինքն՝ որ այդ թվերը իրականում հանդիսանում են M-ի որևէ ենթաբազմություն և նրանց գումարը S է։
Քանի որ լուծումը կարելի է արագ ստուգել, խնդիրը պատկանում է NP-դասին։ Դրանից բացի, կա նաև NP-ամբողջական խնդիրների դաս, այսինքն՝ ամենադժվար NP խնդիրների դասը։ Եթե գտնվի «արագ» ալգորիթմ դրանցից գոնե մեկի լուծման համար, ապա դա ավտոմատ կնշանակի, որ ցանկացած NP խնդրի համար նույնպես գոյություն ունի «արագ» ալգորիթմ։ Եվ մեր կողմից դիտարկվող այս խնդիրը հենց NP կարգի խնդիր է։
Նկատենք, որ S գումարով առաջադրանքը M ենթաբազմության համար հանդիսանում է մասանվոր դեպք արհեստական բանականության հնարած խաղի համար։ Պարզապես այս դեպքում խաղը ընթանում է մի տախտակի վրա, որի մի կողմը 1 է։ Այսինքն՝ եթե իսկապես գոյություն ունի լավ ալգորիթմ, ապա մարդու համար այն գտնելը, ամենայն հավանականությամբ, դժվար կլինի, առավել ևս՝ ժամանակակից արհեստական բանականության համար։ Մնում է պարզապես ինչ-որ եղանակով տարբերակներ փորձել։ Նմանատիպ խնդիրները ամբողջությամբ NP դասի են։ Օրինակ՝ սուդոկու խաղը նույնպես այդ դասից է։ Այնպես որ կարող ենք վստահ լինել, տախտակի վրա թվերը ի հայտ են գալիս պատահական, և «լուծումը» նույնպես ընտրվում է պատահական։ Հետևաբար հնարավոր է, որ ինչ-որ մակարդակում լուծման կոմբինացիան կլինի ոչ միակը, և դա, իհարկե, այնքան էլ լավ չէ։ Չէ՞ որ այդ դպքում ստիպված կլինենք ինչ- որ պահի գործել պատահականության սկզբունքով։
Ամփոփենք մեր դատողությունները՝ նշելով, որ արհեստական բանականությունը պետք է օգտագործել «մարդկային խելքով», այլ ոչ թե հուսալ որ նա կատարյալ է։ Այնուամենայնիվ, հրաշալի է, որ այն կարող է մտածող մարդուն այսքան շատ նյութ տալ խորհելու համար։ Պատկերացրեք՝ որքան ընդհանրացումներ կարելի է անել այս խաղի հիման վրա։ Ավարտելով նշենք, որ քննարկվող խաղը արդեն նախկինում հորինված էր։ Այնպես որ, հայտնի չէ՝ արհեստական բանականությունը ի՞նքն է հորինել այդ կանոնները, թե՞ ամեն դեպքում օգտվել է։
Առաջադրանքներ՝
3. Դիսկրետ տոմոգրաֆիայի խնդրում լուծման միակության միակ խոչընդոտը «շախմատային քառյակների» գոյությունն էր։ Բերե՛ք արհեստական բանականության կողմից առաջադրված խնդրի լուծման միակությանը խանգարող խոչընդոտներ, որոնք կարող են առաջանալ խնդիրը լուծելիս։
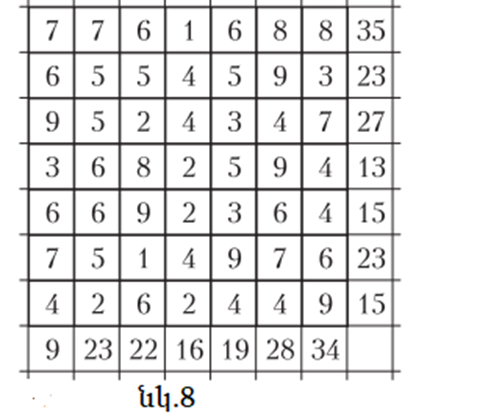
4. Արհեստական բանականության կողմից առաջարկած լուծումն արդյո՞ք միակն է (նկ․ 8)։
Գրականություն
1. Հ․ Ջ․ Ռայզեր, «Զրոներով և մեկերով մատրիցաների կոմբինատոր հատկությունները» , մաթեմատիկական կանադական ամսագիր, 2010թ․, № 9, էջ 269–275,
2. Դ․ Վ․ Մուսատով, « Հաշվելու բարդությունը», ՄՊՖՏԻ, 2016թ․,
3. Հղում՝ https:www.digitaltrends.comgaming sumplete-chatgpt-ai-game-design-ethics ։
Հեղինակ՝ Ա․ Բոլոտին
Թարգմանությունը՝ Լիանա Հակոբյանի
Աղբյուրը՝ այստեղ։

